本课程来自
深度之眼,部分截图来自课程视频。
【第四章 最优化理论】4.1无约束最优化
在线LaTeX公式编辑器
任务详解:
这节课主要介绍了梯度下降法,牛顿法,牛顿法收敛速度等知识点。
掌握目标:
1、掌握梯度下降法
2、了解牛顿法,拟牛顿法
3、了解梯度下降和牛顿法的收敛速度以及优缺点
无约束优化(用得最多)
无约束优化问题是机器学习中最普遍、最简单的优化问题。
x∗=minxf(x),x∈Rn
求最大值也可以 在前面加上负号,变成上面求最小的形式。
梯度下降法
求一个函数f(x)的最小值一般有两种方式:
①对函数f(x)求导并使其等于0(或者说使得梯度
▽f(x)等于0),但是很多复杂的函数求导后没法求出解,所以这种方法实际上很少用。
② 基于迭代的方法,从某个点
x0开始找很多点
x0→x1→x2⋯,使得这些点满足:
f(x0)>f(x1)>f(x2)⋯,且有
x1=x0−λ∣▽f(x0)∣▽f(x0),这里
∣▽f(x0)∣▽f(x0)表示的是单位梯度,主要是方向(梯度的方向下降最猛),有时候懒人就直接写
▽f(x0),方向前面乘上
λ就是步长,所以写成:
x1=x0−λ▽f(x0)。通项就是:
xn+1=xn−λ▽f(xn)
---------------------------------------------------------割你没商量1------------------------------------------------------
下面用数学的方法来估计一下步长
λ,记
f(xn+1)=f(xn−λ▽f(xn))=g(λ)
这是一个关于
λ的函数,要使得步长小一些(如果步长太多就会无法到达最低点),就是要求函数的最小值,就是求导数并等于0:
g′(λ)=f′(xn−λ▽f(xn))(−▽f(xn))=0
然后看如何解出
λ。
实际上
λ也不会取很大,一般是
10−3∼10−4
---------------------------------------------------------割你没商量1------------------------------------------------------
对于整体的损失函数而言:
J(w)=J(x1,w)+J(x2,w)+...+J(xn,w)
如果n比较大,则每次计算梯度的时候都要把这些样本求和,再计算,运算很慢,所以有:
随机梯度下降
从
w0→w1的梯度,只用第一个样本和输出
x1,y1来计算
J(x1,w)
从
w1→w2的梯度,只用第二个样本和输出
x2,y2来计算
J(x2,w)
每一次只用一个样本来进行梯度计算虽然速度很快,但是会受到每一个样本的影响会很大,很容易被异常样本把结果带偏。因此出现了:
batch梯度下降
取batch size=100,
从
w0→w1的梯度,使用
x1∼x100来计算
J(w)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧J(x1,y1,w)J(x2,y2,w)⋮J(x100,y100,w)
从
w0→w1的梯度,使用
x101∼x200来计算
J(w)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧J(x101,y101,w)J(x102,y102,w)⋮J(x200,y200,w)
所有的样本都算完,就是已给epoch。
牛顿法(两种解释)
解释一
之前提过:求一个函数f(x)的最小值可以对函数f(x)求导并使其等于0(或者说使得梯度
▽f(x)等于0):
f′(x)=0
把函数f(x)的导数看做一个函数,令
g(x)=f′(x)⇒g(x)=0
用牛顿法求这个使得
g(x)=0的过程也是已给迭代的过程

假设
g(x)的函数曲线是这个样子,要找到那个
g(x)=0的点,先做某个
xn的切线,然后找到切线与x轴相交的点
xn+1然后再做
xn+1的切线,以不断逼近
g(x)=0的点。
先来求第一条切线的方程:
y−g(xn)=g′(xn)(xn+1−xn)
令y=0(就是上图中的
xn+1点)
−g(xn)=g′(xn)(xn+1−xn)xn+1−xn=−g′(xn)g(xn)xn+1=xn−g′(xn)g(xn)
再把
g(x)=f′(x)带回来
xn+1=xn−f′′(xn)f′(xn)
这是二维的情况,如果是多维的情况:
xn+1=xn−H−1▽f(xn)
其中H是海神矩阵,除以海神矩阵就是乘以它的逆矩阵。为什么这里是海神矩阵?因为
xn+1是
Rn的。
▽f(xn)是n维向量,二次求导就是海神矩阵。
在机器学习中,要算海神矩阵的逆矩阵很麻烦,于是就引申出了很多种拟牛顿法BFGS(用另外一个矩阵来逼近海神矩阵的逆矩阵)。
解释二
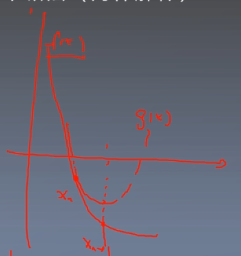
如上图所示,函数f(x)是一个复杂的曲线,然后在点
xn上用一个二次函数g(x)进行拟合,然后找到g(x)最低点
xn+1,然后把
xn+1代入f(x)继续拟合,不断迭代,直到取到f(x)的最小值,具体的计算过程如下:
先写出g(x)在
xn的泰勒展开,只用写到二次项:
g(x)=f(xn)+f′(xn)(x−xn)+2f′′(xn)(x−xn)2+...
g(x)是二次函数,可以写为
ax2+bx+c,那么最低点
xn+1可以看做最小值,根据初中的知识可以知道,最小值为:
x=2ab
a是泰勒展开的二次项的系数,b是一次项的系数,把泰勒展开再展开,合并系数得:
a=2f′′(xn)
b=f′(xn)−xnf′′(xn)
因此最低点
xn+1的值为:
xn+1=−f′′(xn)f′(xn)−xnf′′(xn)=xn−f′′(xn)f′(xn)(1)
这个和解释一推导出来的公式是一样的。
牛顿法要拟合,因此不能离最小值太远的地方拟合,要接近极小值再拟合收敛的效果越好。因此经常是先用梯度下降,到了局部极小值附近后再用牛顿法。
牛顿法收敛速度
按这个迭代原理,
x0就应该是函数的局部最优点,也就是
f(x0)有最小值,且有
f′(x0)=0
要弄明白这个收敛速度,就是要比较下
xn+1到
x0的距离和
xn到
x0的距离的区别(把公式1代入下面):
∣xn+1−x0∣=∣xn−f′′(xn)f′(xn)−x0∣
由于
f′(x0)=0,所以分子加上
f′(x0)不影响。
=∣xn−f′′(xn)f′(xn)−f′(x0)−x0∣
根据中值定理
f(b)−f(a)=(b−a)f′(ξ),a<ξ<b,分子有:
=∣∣∣∣xn−f′′(xn)(xn−x0)f′′(ξ)−x0∣∣∣∣
=∣xn−x0∣∣∣∣∣1−f′′(xn)f′′(ξ)∣∣∣∣
=∣xn−x0∣∣∣∣∣f′′(xn)f′′(xn)−f′′(ξ)∣∣∣∣
再搞一次拉格朗日中值定理:
=∣xn−x0∣∣∣∣∣f′′(xn)(xn−ξ)f′′′(η)∣∣∣∣
令
∣M=∣∣∣∣f′′(xn)f′′′(η)∣∣∣∣
=∣xn−x0∣∣(xn−ξ)∣M
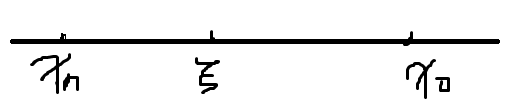
如上图所示,
ξ是在
xn∼x0之间的,所以
∣xn−x0∣∣(xn−ξ)∣M<(xn−x0)2M
由于M的分子分母都是导数,导数都是有界的,所以M是有界的,用
M表示其上界。
∣xn−x0∣∣(xn−ξ)∣M<(xn−x0)2M<(xn−x0)2M
也就是:
∣xn+1−x0∣<(xn−x0)2M
当
xn和x0的距离小于1:
(xn−x0)<1,则
(xn−x0)2<<1,说明是按照平方的速度进行收敛的,注意这里有条件:
xn和x0的距离小于1,如果距离大于1,上界会越来越大,没法收敛。



