正则的详细解释以及灵活运用（包含Lasso）

正则的介绍

正则一开始是用来限制参数的，例如在逻辑回归中，目标函数： $p(y=1|x;w)=\dfrac{1}{1+e^-{w^Tx+b}}$越大越好参数， $p(y=0|x;w)=1-\dfrac{1}{1+e^-{w^Tx+b}}$越小越好，如果我们的数据线性可分时， 根据目标函数， $w$就会变得无穷大，因为此时 $p(y=1|x;w)=1$而 $p(y=0|x;w)=0$,但是这显然不是我们想要的，这样模型就会过拟合了。所以我们要限制参数，不让它太大因此这个时候我们用到了正则：

$w,b=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)+\lambda||w||^2$

$||w||^2=w_1^2+w_2^2+w_3^2+...+w_d^2$

假设 $w$变得很大，那么 $\lambda||w||^2$也会变得很大，这样就会使公式也会变得很大，而我们的目标函数是为了求最小，所以在计算的时候不会让 $w$变得特别大。也就是做到了限制参数的作用。

此时 $\lambda$表示的是超参数，当 $\lambda=0$时表示没有任何限制，
当 $\lambda$越大对 $w$的限制越大，相反当 $\lambda$越小对 $w$的限制越小。因此 $\lambda$限制 $w$避免线性可分时参数 $w$变得无穷大。

L1和L2

$\lambda ||w||^2$我们经常称为 $L2$,，但是正则不仅仅只有 $\lambda ||w||^2$一种，我们常见的还有正则 $L1:\lambda ||w||=\lambda\sum_{i=1}^d|w_i|$当然还有其他正则在这里就不一一介绍啦，一般正则的使用都是比较灵活，针对特定的问题使用正则。

现在我们了解一下这两种正则

$w,b=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)+\lambda||w||^2_2$

$w,b=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)+\lambda||w||_1$

$L1$和 $L2$的作用都是使得参数 $w$变小，避免变得很大，但是它俩有一个不同之处：

使用 $L1$导致我们获得解是一个稀疏的解：

$w=(0,0,0,0,0.01,0,0,0,0.2,0,0.4)$

也就是遇到一些很小的值我们都把它设置为0，因此 $L1$可以做一些选择性的场景

而使用使用 $L2$导致我们获得解是不是稀疏的

w=(0.1,0.054,0.11,0.25,0.01,0.2,0.4)

为什么会是这样的

我们使用几何的角度来了解一下如下图：

我们求得解也就是 $f(w)$与 $L1或L2$的交集处，我们可以从图片中看出 $f(w)$与 $L1$的交点有很多都落在 $y$轴上，所以加入L1的正则得到的解往往是稀疏的

因此我们在使用正则的时候往往是根据特定 问题去选择使用L1还是L2，比如我们在思考问题的时候大脑中的的神经不是全部在发生作用，往往只是一小部分，或者只是一部分区域，如果我们在思考这类问题时，可以加入一个L1正则

目标函数为： $f(r_1w_1+r_2w_2+r_3w_3+r_4w_4+...+r_nw_n)$

解： $w(w_1,w_2.w_3...w_n)$

大部分时间思考时我们只有小部分区域可以活动，因此可以使用L1正则

$L1 \quad vs \quad L2$

虽然L1和L2都能使参数变小，但是L2的准确率比L1要高，L1是稀疏的L2不是

L1还有一个缺点：从相似参数里随机选择一个，而不是最好的那个。所以现在有：

$w,b=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)+\lambda_1||w||_1+\lambda_2||w||^2_2$

并且对于超参数 $\lambda_1,\lambda_2$进行不断地优化

对于

$w_1=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)+$
$w_2=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)+\lambda||w||^2_2$

问： $f(w_1)?f(w_2)$

答： $f(w_1)\leq f(w_2)$

为什么会是这样的呢？

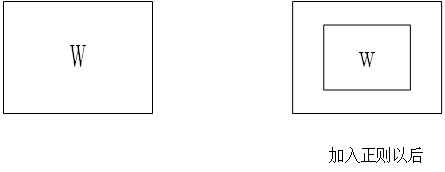
如图我们加入正则以后w可选择的范围变小了。

交叉验证

交叉验证的目的就是选择最优的那个超参数。例如我们选择这样L2正则，那么我们该怎么确定 $\lambda$的值，或者说当 $\lambda$的最优值是什么呢？

$w,b=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)++\lambda||w||^2_2$

这个时候我们一般使用的是交叉验证，也就是将训练数据切出来一小部分为验证数据

假设 $\lambda\in\{0.1,0.2,0.3,0.4\}$

$p$表示使用验证集计算出的准确率

计算当 $\lambda=0.1$时： $p=\dfrac{p_1+p_2+p_3+p_4}{4}$
计算当 $\lambda=0.2$时： $p=\dfrac{p_1+p_2+p_3+p_4}{4}$
计算当 $\lambda=0.3$时： $p=\dfrac{p_1+p_2+p_3+p_4}{4}$
计算当 $\lambda=0.4$时： $p=\dfrac{p_1+p_2+p_3+p_4}{4}$
找到最优的 $\lambda$代入目标函数进行下一步计算

参数的搜索策略

对于： $w,b=argmin\quad\prod_{i=1}^n p(y_i|x_i;w)+\lambda_1||w||_1+\lambda_2||w||^2_2$

我们如何去选择 $\lambda_1$和 $\lambda_2$

现在有4种常见的解决方式：
① grid search

假设 $\lambda_1\in\{0.1,0.2,0.3,0.4\}$

假设 $\lambda_2\in\{0.32,0.32,0.23,0.14\}$

考虑所有的组合

利用交叉验证求平均准确率，找到最合适的那个组合

优点：可以平行化计算。

缺点：计算复杂，浪费资源

② 随机 search ：给定 $\lambda_1$和 $\lambda_2$从该区间随机取出数据

③遗传算法：好的个体更倾向产生更好的个体，不断地去选择更好的 $\lambda$

④贝叶斯优化：类似与遗传算法，去不断选择更好的区间， 其核心思想是好的参数周围也会产生更好的参数，差点的参数周围也不太好，不断的选择更好的参数。

参数的搜索策略也是比较重要的：
比如神经网络的每一层都包含超参数，怎样去选择更好的参数也是一个比较重要的地方(调参)

正则的灵活使用

比如刚才提到的大脑的思考问题：我们在思考问题的时候大脑中的的神经不是全部在发生作用，往往只是一小部分，或者只是一部分区域

现在这里有两个条件：

①某个区域只有少部分被激活

②在空间上相邻的作用也类似。

old： $minmize \quad f(w)$

new: $minmize \quad f(w) +\sum_{i=1}^n \lambda_i||w_i||+\sum_{i=1}^n\sum_{j=1}^r||w_{ij}-w_{ij-1}||^2$

推荐系统：

将用户-商品矩阵分解成用户矩阵和商品矩阵

我们的目标函数是：
$min \sum_{(ij)\in\Omega}(r_{ij}-u_iv_j)^2+\sum_{i=1}^n \lambda_i||u_i||+\sum_{i=1}^m \lambda_i||v_i||$

$u_i$表示用户， $v_i$表示商品 $r_{ij}$表示用户实际喜欢的商品，后面加入对于 $u$和 $v$的正则

现在我们又考虑到时间这个维度也就是说，随着时间的推移，用户对于产品的喜爱程度可能会发生变化，但是不会发生太大的变化，因此我们加入新的正则：

$min \sum_{t=1}^T\sum_{(ij)\in\Omega}(r_{ij}^t-u_i^tv_j^t)^2+\sum_{t=1}^T\sum_{i=1}^n \lambda_{it}||u_i^t||+\sum_{t=1}^T\sum_{i=1}^m \lambda_{it}||v_i^t||+\sum_{t=1}^T\sum_{i=1}^m \lambda_{it}||v_i^t-v_i^{t-1}||$

$+\sum_{t=1}^T\sum_{i=1}^n \lambda_{it}||u_i^t-u_i^{t-1}||$

所以添加正则的作用目的就是防止过拟合的一种手段

选择超参数时使用的是交叉验证

参数搜索比较消耗资源。

MLE和MAP

为什么在这里提到MLE和MAP，因为今天我们学习了正则，在很多情况下MAP相当于MLE的+正则，为什么会是这样呢？我们来推导一下

MLE: $argmax:p(D|\theta)$

MLE: $argmax:p(\theta|D)=argmax p(D|\theta)\cdot p(\theta)\quad$(对于 $p(x)$数据的概率我们一般不用考虑)

其实 $p(\theta)$就是一个先验的概率，随着样本的增加，先验的作用越来越小。

假设我们的 $p(\theta)$服从高斯分布也就是：

$p(\theta)=\dfrac{1}{\sqrt{2\pi}\sigma}\cdot e^{-\dfrac{\theta^2}{2\sigma^2}}$

$logp(\theta)=-log2\pi\sigma-\dfrac{\theta^2}{2\sigma^2}$
现在我们计算：

$argmax:log p(\theta|D)=log p(D|\theta)+logp(\theta)=log p(D|\theta)-log2\pi\sigma-\dfrac{\theta^2}{2\sigma^2}$

将与 $\theta$无关的项去掉：

$MAP:\quad argmax:log p(\theta|D)=log p(D|\theta)-\dfrac{1}{2\sigma^2}||\theta||^2$

$MLE:\quad argmax:log p(D|\theta)$

所以这里的 $\lambda=-\dfrac{1}{2\sigma^2}$

如果 $p(\theta)$服从高斯分布，MAP相对于MLE来说就是增加了一个L2正则

假设我们的 $p(\theta)$服从拉普拉斯分布也就是：

$p(\theta)=\dfrac{1}{2b}\cdot e^{\dfrac{\theta}{-b}}$
现在我们计算：

$argmax:log p(\theta|D)=log p(D|\theta)+logp(\theta)=log p(D|\theta)-log\dfrac{1}{2b}-\dfrac{1}{b}||\theta||$

将与 $\theta$无关的项去掉：
$MAP:\quad argmax:log p(\theta|D)=log p(D|\theta)-\dfrac{1}{b}||\theta||$

$MLE:\quad argmax:log p(D|\theta)$

如果 $p(\theta)$服从拉普拉斯分布，MAP相对于MLE来说就是增加了一个L1正则

总结：

高斯:L2正则

拉普拉斯：L1正则

Lasso介绍

Lasso模型其实就是在线性回归的基础上+L1正则主要是用来进行特征的提取，为什么会使用Lasso呢：

主要有一下几方面的原因：

1、数据量太少容易产生过拟合

2、维度太高计算量太高

3、可解释性

我们知道加了L1正则我们计算出的解是稀疏的，也就可以确定哪项权重对于数据是比较重要的。对于特征提取是比较有帮助的。

预测房价：
假设现在有5个特征： $f=(f_1,f_2,f_3,f_4,f_5)$

我们现在计算那些特征的组合对于房价是比较重要的

第一种方法穷举法：
计算 $\{f_1\}=acc_1$, $\{f_2\}=acc_2$, $\{f_3\}=acc_3.$ $\{f_4\}=acc_4,$ $\{f_5\}=acc_5,$ $\{f_1,f_2\}=acc_6....$以此类推把所有特征组合都考虑，选择最高的acc

很明显这样做计算量比较大，但求出来的解是全局最优解。

第二种方法：贪心算法
先选择最好的：
$\{f_1\}=acc_1$, $\{f_2\}=acc_2$, $\{f_3\}=acc_3.$ $\{f_4\}=acc_4,$ $\{f_5\}=acc_5$j
假设, $acc_2$最大，

下面我们计算 $\{f_2，f_1\}=acc_1,$ $\{f_2，f_3\}=acc_2,$ $\{f_2，f_4\}=acc_3,$ $\{f_2，f_5\}=acc_4$

再次找到最好的并与上一个相比，如果比上一个好继续，比上一个差终止。

或者计算
$(f_1,f_2,f_3,f_4,f_5)=acc$

然后删掉一个进行计算，找到最好的与原来进行相比，好就替代然后重复删除一个，不好就会终止。
这样我们计算的可能不是全局最优解，只是局部最优解。

使用Lasso的方法

我们可以知道Lasso是线性回归+L1正则，那么现在有一个问题。我们在计算梯度的时候需要计算：

$\dfrac {\partial |w| }{\partial w _{i}}$我们知道对 $|w|$求导是比较麻烦的，并且 $w$还是是多维的

因此我们使用到了coordinate descent

coordinate descent

也就是说对于 $g(w)=g(w_1,w_2,w_3,....,w_n)$我们在对于 $w_1$进行求导时将其他维度的值看作常量，因此不断的对其中的 $w_i$进行求导，也就是每个维度都单独的去考虑，寻找针对这个维度的最优解。

这个算法不一定对所有模型可以求得很好的结果，但是在Lasso中它很快会收敛。而且我们不用设置步长

Lasso

我们使用线性回归+L1正则，公式:

$\varphi=\sum_{i=1}^n(\sum_{j=1}^dw_jx_{ij}+b-y_i)^2+\lambda\sum_{j=1}^d|w_j|$

$x_{ij}$表示第i个样本中的第j个特征

$\dfrac{\partial \varphi}{\partial w_\varphi}=2\sum_{i=1}^n(\sum_{j=1}^dw_jx_{ij}+b-y_i)\cdot x_{i\varphi}+\lambda\dfrac{\partial |w|}{\partial w_\varphi}$

$=2\sum_{i=1}^n(\sum_{j\neq\varphi}w_jx_{ij}+b-y_i+w_\varphi x_{i\varphi})\cdot x_{i\varphi}+\lambda\dfrac{\partial |w|}{\partial w_\varphi}$

$=2\sum_{i=1}^n(\sum_{j\neq\varphi}w_jx_{ij}+b-y_i)\cdot x_{i\varphi}+2w_\varphi\sum_{i=1}^n x_{i\varphi}^2+\lambda\dfrac{\partial |w|}{\partial w_\varphi}$

令 $2\sum_{i=1}^n(\sum_{j\neq\varphi}w_jx_{ij}+b-y_i)\cdot x_{i\varphi}=C_\varphi$

$2w_\varphi\sum_{i=1}^n x_{i\varphi}^2=w_\varphi A_\varphi$

$\dfrac{\partial \varphi}{\partial w_\varphi}=C_\varphi+w_\varphi A_\varphi +\lambda\dfrac{\partial |w|}{\partial w_\varphi}$

对于 $\dfrac{\partial |w|}{\partial w_\varphi}$我们分为3种情况，也就是 $w_\varphi>0,$ $w_\varphi<0,$和 $w_\varphi=0$令导数等于零

$\begin{cases}c_\varphi+w_\varphi A_\varphi+\lambda \quad\quad w >0\rightarrow\quad w_\varphi=\dfrac{-c_\varphi-\lambda}{A_\varphi}>0\rightarrow C_\varphi<-\lambda\\ [c_\varphi-\lambda, c_\varphi+\lambda]\quad\quad w =0\rightarrow-\lambda\leq C_\varphi\leq\lambda\\ c_\varphi+w_\varphi A_\varphi-\lambda \quad\quad w <0\rightarrow\quad w_\varphi=\dfrac{-c_\varphi+\lambda}{A_\varphi}>0\rightarrow C_\varphi>\lambda\end{cases}$

因此：对于每个维度参数 $w_\varphi$的更新
$w_\varphi=\begin{cases}\\\dfrac{-c_\varphi-\lambda}{A_\varphi}\quad\quad C_\varphi<-\lambda\\0\quad\quad -\lambda\leq C_\varphi\leq\lambda\\\dfrac{-c_\varphi+\lambda}{A_\varphi}\quad\quad C_\varphi>\lambda\end{cases}$