Chapter.3 Divide and Conquer

Divide&Conquer

1. Divide--> Divide the problem(instance) into one or more subproblem.
2. Conquer--> Conquer each subproblem
3. Combine--> Combine the solutions of the subproblems into the solutions of the whole big problem.

Examples

ex.1— mergeSort

1.Divide--> Divide an array into two subarrays.
2.Conquer-->Sort each subarray recursively.
3.Combine-->Merges two ordered subarrays.

Running time:
T(n)=2T(n/2)+Θ(n)
T(n)= Θ(nlgn)

package nov16;
import java.util.Arrays;
//A java version for mergeSort algorithm
public class MergeSortTester 
{
	public static void main(String[]args)
	{
		int[] list = {1,10,2,5,8,7,9,6};
		mergeSort(list,0,list.length-1);
		//oneMergeSort(list,0,(0+list.length)/2,list.length-1);
		System.out.print(Arrays.toString(list));
	}
	public static void mergeSort(int[] A,int start,int end)
	{
		if(start<end)
		{
			int mid = (end+start)/2;
			mergeSort(A,start,mid);
			mergeSort(A,mid+1,end);
			oneMergeSort(A,start,mid,end);
		}
	}
	public static void oneMergeSort(int[] A,int left,int mid,int right)
	{
		int[] temp = new int[A.length];
		int p = left,m = mid+1,k=left;
		// Throw a smaller elements from A to temp by using two pointer 
		while(p<=mid && m<=right)
		{
			if(A[p]>=A[m]) {temp[k++]=A[m++];}
			else {temp[k++]=A[p++];}
		}
		// If the pointer p does't arrive at mid, copy the remain to temp
		while(p<=mid) {temp[k++]=A[p++];}
		// Same as above
		while(m<=right) {temp[k++]=A[m++];}
		// Update initial A by temp
		for(int i=left;i<=right;i++){A[i] = temp[i];}
	}
}

ex.2—binarySearch

1.Divide-->Compare the number X with the middle element of the array to get the subarray in which X resides.
2.Conquer-->Look up X in this subarray recursively 
3.Combine-->Nothing to do.

Running time:
T(n)=2T(n/2)+Θ(1)
T(n)= Θ(lgn)

package nov11;

public class BinarySerach
{
	public static void main(String[] args)
	{
		int[] a = {1,3,5,7,9,10};
		int index = new BinarySerach().binarySearch(a, 5);
		System.out.println(index);
	}
	
	public int binarySearch(int[] a, int key)
	{
		int left = 0;
		int right = a.length - 1;
		int mid = (left+right)/2;
		
		while(left<right)
		{
			if(a[mid]>key)
			{
				right = mid - 1;
			}
			else if(a[mid]<key){
				left = mid+1;
			}else {
				return mid;
			}
			mid = (left+right)/2;
		}
		return -1;
	}
}

ex.3—powering a number

Idea:

x to n is (x to n over 2) times (x to n over 2) if n is a even number;
x to n is (x to (n-1)/2) times (x to (n-1)/2) times x if n is an odd number.

1. Divide--> Divide the n to n/2 or (n-1)/2 corresponding to n's odevity.
2. Conquer--> Calculate the two exponents separately.
3. Combine-->  Multiply the exponents which has been calculated.

Running time:
T(n)=2T(n/2)+Θ(1)
T(n)= Θ(lgn)

package nov11;

public class DoubleSquareTester 
{
	public static void main(String[] args) {
		int n = 20;
		double sum=0;
		long t1 = System.nanoTime();
		//new DoubleSquareTester().go(sum,0,n-1);
		sum += Math.pow(2, n);
		long t2 = System.nanoTime();
		System.out.println(t2-t1);
	}
	
	void go(int sum,int start,int end)
	{
		if(start<end)
		{
			int mid = (start+end)/2;
			go(sum,start,mid);
			go(sum,mid+1,end);
			sum = combine(sum,start,end);
			//System.out.println(sum);
		}
	}
	
	int combine(int sum,int start,int end)
	{
		sum += Math.pow(2,end-start+1);
		return sum;
	}
}

ex.4—Fibonacci numbers

Baseline：
    Fn=0           （n=0）
    Fn=1           （n=1）
    Fn=F(n-1)+F(n-2)（n>=2）
    running time： Ω(φ^n)  φ=(1+5^(1/2))/2。
Bottom-up：
    calaulate F0，F1，F2 …… Fn in order。
    running time：Θ(n)。
Naive square recurrence：
    Fn=φ^n/5^(1/2)  for a closet integer。
    running time：Θ(lgn)。
   The values in this algorithm are limited by the number of computer bits as floating-point Numbers，thus cannot be done with computer code.
square matrix recurrence：
    (F(n+1)  Fn)  = (1 1)n
    (Fn  F(n-1))    (1 0)
    running time：Θ(lgn)
 We can use inducation for proof as shown belowed.
1. (F2  F1)  = (1 1)1
   (F1  F0)    (1 0)
2. (F(n+1)  Fn)  = (Fn      F(n-1)) (1 1)
   (Fn  F(n-1))    (F(n-1)  F(n-2)) (1 0)

Matrix multiplication

Input:matrix A[aij],matrix B[aij](i,j = 1,2,3,4,...,n)
Output:matrix C = A*B where cij = sum of A‘s ith row products B's jth column.
psedocode:
    for i ← 1 to n
    do for j ← 1 to n
        cij=0
        do for k ← 1 to n
            do cij ← cij+aik·bkj
    running time:Θ(n^3)

package nov16;
import java.util.*;
public class MatrixMultiplicationTester 
{
	public static void main(String[] args) {
		int a[][] = new int[6][6];
		int b[][] = new int[6][6];
		
		for(int i=0;i<a.length-1;i++)
		{
			for(int j=0;j<a[0].length-1;j++)
			{
				a[i][j] = (int)(Math.random()*10); 
				b[i][j] = (int)(Math.random()*10); 
			}
		}
		System.out.println("A:");
		for(int i=0;i<a.length-1;i++)
		{
			System.out.println(Arrays.toString(a[0]));
		}
		System.out.println("B:");
		for(int i=0;i<a.length-1;i++)
		{
			System.out.println(Arrays.toString(b[0]));
		}
		int[][] result = matrixMultiple(a,b);
		System.out.println("Result:");
		for(int i=0;i<result.length-1;i++)
		{
			System.out.println(Arrays.toString(result[0]));
		}
		
	}
	
	public static int[][] matrixMultiple(int A[][],int B[][])
	{
		// Determine if the number of columns in matrix A is the same as the number of rows in matrix B
		if(A[0].length != B.length)
		{
			System.out.println("Matrix A cannot multiple matrix B!!");
			return null;
		}
		int C[][] = new int[A.length][B[0].length];
		for(int rowC=0;rowC<C.length;rowC++)
		{
			for(int columnC=0;columnC<C[0].length;columnC++)
			{
				C[rowC][columnC] = 0;
				for(int i=0;i<B.length-1;i++)
				{
					C[rowC][columnC] += A[rowC][i]*B[i][columnC];
				}
			}
		}
		return C;
	}
}

Matrix block multiplication

Idea:Regard an n by n matrix as a 2 by 2 partitioned matrix of n/2n/2 submatrix.
C = AB can divided into 22 submatrix as belowed.

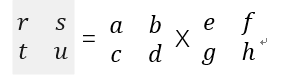
where r->ae+bg,s->af+bh,t->ae+ug,u->cf+dh
T(n) = 8T(n/2)+o(n2)

Strassen’s Algorithm for Fibonacci numbers

Idea:To avoid multipliaction, utilize add to reduce multiplication operations

P1 = a*(f-h);
P2 = (a+b)*h;
P3 = (c+d)*e;
P4 = d(g-e);
P5 = (a+d)(e+h);
P6 = (b-d)(g+h);
P7 = (a-c)(e+f);
then we obtain->
r = P5+P4-P2+P6;
s = P1+p2;
t = P3+p4;
u = P5+P1-P3-P7;