2.6 空间曲线及其方程
一、球面
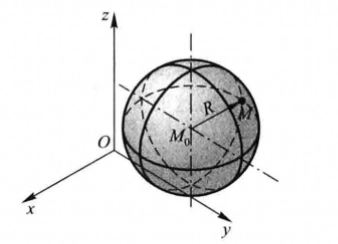
空间坐标系中有一球面,球心在点 \(M0(x_0,y_0,z_0)\),半径为 \(R\)
设 \(M(x,y,z)\) 是球面上任意一点,则有:\(∣M_0M∣=R\)
展开即为球面标准方程:\(\sqrt{{(x-x_0)}^2+{(y-y_0)}^2+{(z-z_0)}^2}=R\)
或 \(Ax^2+Ay^2+Az^2+Dx+Ey+Fz+G=0\)
二、旋转曲面
一条平面曲线绕其平面上的一条直线旋转一周所成的曲面叫做旋转曲面,旋转曲线和定直线依次叫做旋转曲面的母线和轴。
空间中一曲线的方程表示为:\(f(x,y,z)=0\)
由于平面曲线通常在坐标面上,所以 \(x,y,z\) 三个坐标中通常有一个为 \(0\) 。
例如(其他情况同理类推):当曲线 \(C\) 在 \(yOz\) 坐标面上时 \(x=0\)
所以此时曲线方程表示为:\(f(y,z)=0\)
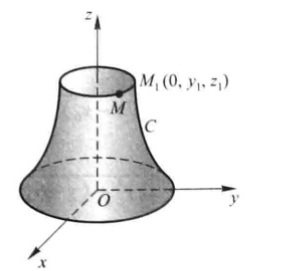
设 \(M_1(0,y_1,z_1)\) 为曲线 \(C\) 上任意一点,则有:\(f(y_1,z_1)=0\)
当曲线 \(C\) 绕 \(z\) 轴旋转时,设旋转到任一点 \(M(x,y,z)\),在旋转的过程中,\(z\) 保持不变,\(x,y\) 不断变化
且有:\(d_{z\rightarrow m}=\sqrt{x^2+y^2}=|y_1|\)
所以有:\(y_1=\pm \sqrt{x^2+y^2}\)
带入 \(f(y_1,z_1)=0\) 可得:\(f(\pm \sqrt{x^2 +y^2}, z) = 0\)
同理可知,当曲线 \(C\) 绕 \(y\) 轴旋转时,形成的曲面方程为:\(f(y, \pm \sqrt{x^2 + z^2}) = 0\)
三、柱面
一般柱面: (例:母线平行于 \(z\) 轴、准线垂直于 \(z\) 轴):
(例:母线平行于 \(z\) 轴、准线垂直于 \(z\) 轴) \(x^2+y^2=R^2\)
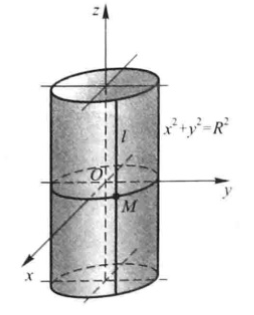
( \(xOy\) 面上的圆$ x2+y2 = R^2$ 即是柱面的准线,直线 \(l\) 即是柱面的母线)
抛物柱面:
\(y^2=2x\)
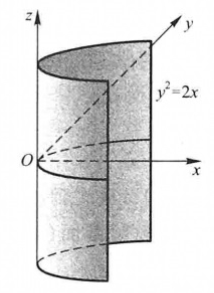
其他柱面以类似
4、二次曲面
二次曲面:可以由三元二次方程表示的曲面称为二次曲面,平面称为一次曲面。
①椭圆锥面
x2a2+y2b2=z2 \frac{x2}{a2} + \frac{y2}{b2} = z^2
a
2
x
2
+
b
2
y
2
=z
2
②椭球面
x2a2+y2b2+z2c2=1 \frac{x2}{a2} + \frac{y2}{b2} + \frac{z2}{c2}= 1
a
2
x
2
+
b
2
y
2
+
c
2
z
2
=1
③旋转单叶双曲面(一个减号):
x2+y2a2−z2c2=1 \frac{x^2 + y2}{a2} - \frac{z2}{c2} = 1
a
2
x
2
+y
2
−
c
2
z
2
=1
④旋转双叶双曲面(两个减号):
x2a2−y2+z2c2=1 \frac{x2}{a2} - \frac{y^2 + z2}{c2} = 1
a
2
x
2
−
c
2
y
2
+z
2
=1
⑤椭圆抛物面
x2a2+y2b2=z \frac{x2}{a2} + \frac{y2}{b2} = z
a
2
x
2
+
b
2
y
2
=z
⑥双曲抛物面
x2a2−y2b2=z \frac{x2}{a2} - \frac{y2}{b2} = z
a
2
x
2
−
b
2
y
2
=z
⑦椭圆柱面
x2a2+y2b2=1 \frac{x2}{a2} + \frac{y2}{b2}=1
a
2
x
2
+
b
2
y
2
=1
⑧双曲柱面
x2a2−y2b2=1 \frac{x2}{a2} - \frac{y2}{b2}=1
a
2
x
2
−
b
2
y
2
=1
⑨抛物柱面
x2=ay x^2 = ay
x
2
=ay
$