文献阅读 - Searching and Mining Trillions of Time Series Subsequences under Dynamic Time Warping

Searching and Mining Trillions of Time Series Subsequences under Dynamic Time Warping

---

T. Rakthanmanon, B. Campana, A. Mueen, et al., Searching and Mining Trillions of Time Series Subsequences under Dynamic Time Warping, KDD (2012) (Best Paper)

---

预备知识

动态时间规整

$\mathbf{t}$、 $\mathbf{r}$分别为 $m$、 $n$维时间序列（time series）

$\mathbf{t} = [t_{1}, t_{2}, \cdots, t_{m}]$

$\mathbf{r} = [r_{1}, r_{2}, \cdots, r_{n}]$

动态时间规整（dynamic time warping，DTW）：利用动态规化（DP）计算距离最小的最佳映射，“时间扭曲”是指为计算最佳映射，需要在时间上压缩或扩展（compress or expand in time）。

规整路径（mapping path）： $\{(p_{1}, q_{1}), (p_{2}, q_{2}), \cdots, (p_{k}, q_{k})\}$，使 $\sum_{i = 1}^{k} | t(p_{i}) - r({q_{i}}) |$最小，且满足

• 边界条件（boundary conditions）： $(p_{1}, q_{1}) = (1, 1)$、 $(p_{k}, q_{k}) = (m, n)$

• 局部约束（local constraint）：路径上任意节点 $(i, j)$，其候选节点（fan-in node）为 $(i − 1, j)$， $(i, j − 1)$， $(i − 1,j − 1)$。该约束保证映射路径单调非减（monotonically non-decreasing）。且对于 $\mathbf{t}$中的任意元素， $\mathbf{r}$中至少有一个元素与之对应，反之亦然。

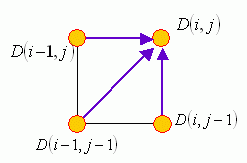
DTW计算（前向DP）：

1. 最优值函数（optimum-value function）： $D (i, j)$为 $\mathbf{t} (1 : i)$与 $\mathbf{r} (1 : j)$间的DTW距离

2. 初始条件： $D (1, 1) = | t(1) - r(1) |$，递归（ $\text{for} \ 1 \leq i \leq m, 1 \leq j \leq n$）：

$D (i, j) = | t(i) - r(j) | + \min \begin{Bmatrix} D (i - 1, j) \\ D (i - 1, j - 1) \\ D (i, j - 1) \end{Bmatrix}$

3. 输出 $D (m, n)$

实现：构造 $m \times n$维的矩阵 $\mathbf{D}$，将初始条件填入 $\mathbf{D} (1, 1)$，然后根据递归公式逐列（行）填充矩阵。计算时间复杂度为 $\mathcal{O}(m n)$。

DTW计算（反向DP）：

1. 最优值函数（optimum-value function）： $D (i, j)$为 $\mathbf{t} (i : m)$与 $\mathbf{r} (j : n)$间的DTW距离，

2. 初始条件： $D (m, n) = | t(m) - r(n) |$，递归（ $\text{for} \ m \geq i \geq 1, n \geq j \geq 1$）：

$D (i, j) = | t(i) - r(j) | + \min \begin{Bmatrix} D (i + 1, j) \\ D (i + 1, j + 1) \\ D (i, j + 1) \end{Bmatrix}$

3. 输出 $D (1, 1)$

DTW距离不满足距离三角不等式且计算时间复杂度高。

DTW下界距离（lower bounding）

DTW下界距离：采用计算更简单的距离度量粗略估计DTW距离，通过DTW下界过滤掉不满足相似性要求的序列，提高查询效率

DTW下界距离应满足3个条件：

• 正确性：经下界距离过滤得到的候选集中必须包含所有满足条件的序列，即不允许出现漏报；

• 有效性：下界距离的计算复杂度应尽量低；

• 紧致性（tightness）：下界距离的度量结果应尽量逼近DTW距离，使候选集不至过大，减少后处理计算量

常用DTW下界距离：

LB_Yi：

LB_Kim： $\mathbf{t}$、 $\mathbf{r}$以起始点、结束点为特征构造DTW下界距离， $\mathcal{O}(1)$；、以起始点、结束点最大值点和最小值点为特征构造DTW下界距离， $\mathcal{O}(n)$

LB_Keogh：查询序列（query）的上、下边界序列 ${U, L}$与候选序列（candidate sequence）对应点间欧氏距离较近者作为DTW下界距离， $\mathcal{O}(n)$

LB_Zhu：

LB_GMBR：对时间序列进行分段累积近似，用网格最小边界矩形近似表示查询序列

---

摘要

在DTW距离下，实现大规模数据集上的精确搜索，且比已知欧氏距离（Euclidean distance）搜索算法更快。

1 引言

在大多数时序问题中，动态时间规整（dynamic time warping，DTW）是最佳测度（the best measure），但其过高的计算复杂度限制其应用。

1.1 万亿数据量（A Brief Discussion of a Trillion）

万亿（trillion）： $10^{12}$，已知论文处理时序数据（time series data）规模至多数亿（one hundred million objects）。

1.2 默认条件（Explicit Statement of our Assumptions）

1.2.1 时序子序列必须标准化（Time Series Subsequences must be Normalized）

比较时，除了对整个数据集进行标准化，还需对每个子序列标准化（normalize each subsequence before making a comparison, it is not sufficient to normalize the entire dataset）。

1.2.2 DTM是最佳测度（Dynamic Time Warping is the Best Measure）

经验表明（800余篇论文）：DTM是最佳测度。

1.2.3 任意长度的查询序列无法索引（Arbitrary Query Lengths cannot be Indexed）

当数据集规模超过10亿时，现有技术无法进行任意长度序列的相似性搜索（there are no known techniques to support similarity search of arbitrary lengths once we have datasets in the billions）。

1.2.4 某些数据挖掘问题需要耗时数小时（There Exists Data Mining Problems that we are Willing to Wait Some Hours to Answer）

2 相关工作

本文考虑精确搜索（exact search）

3 背景（Background and Notations）

3.1 定义（Definitions and Notations）

定义1：时间序列（Time Series） $T$， $T = t_{1}, t_{2}, \dots, t_{m}$

定义2：子序列（subsequence） $T_{i, k}$，起始位置为 $i$、长度为 $k$的时间序列， $T_{i, k} = t_{i}, t_{i + 1}, \dots, t_{i + k - 1}, 1 \leq i \leq m - k + 1$

查询序列（query）： $Q$， $n = | Q |$

候选匹配（a Candidate match to a query $Q$）： $C$（子序列 $T_{i, k}$）

定义3：当 $| Q | = | C |$时， $Q$和 $C$之间的欧式距离（Euclidean distance，ED）为

$\text{ED} (Q, C) = \sqrt{\sum_{i = 1}^{n} (q_{i} - c_{i})^{2}}$

欧式距离（一一映射（a one-to-one mapping of the two sequence），Fig. 2）时DTW（一对多映射（one-to-many alignment），Fig. 3）的特例。

DTW对齐：构造 $n \times n$矩阵，矩阵的第 $(i^{\text{th}}, j^{\text{th}})$元素表示 $q_{i}$和 $c_{j}$的ED距离 $d(q_{i}, c_{j})$。

规整路径（warping path） $P$：一组矩阵元素的连续集合（a contiguous set of matrix elements），给出了 $Q$和 $C$之间的映射关系。 $P$的第 $t^{\text{th}}$个元素定义为 $p_{t} = (i, j)_{t}$，则有：

$P = p_{1}, p_{2}, \dots p_{t}, \dots, p_{T}, \ n \leq T \leq 2n - 1$

规整路径必须以矩阵反对角元素的角点作为起点和终点，路径中各步限制在相邻单元中选取且路径点沿时间轴单调增加（start and finish in diagonally opposite corner cells of the matrix, the steps in the warping path are restricted to adjacent cells, and the points in the warping path must be monotonically spaced in time）。

些外，对规整路径各点与对角位置偏移也可作全局限定（constrain the warping path in a global sense by limiting how far it may stray from the diagonal）。如Sakoe-Chiba带（Sakoe-Chiba Band），规整路径不能偏离对角位置 $R$个单元（the warping path cannot
deviate more than R cells from the diagonal）。

4 算法

4.1 现有优化方法（Known Optimizations）

4.1.1 平方距离（Using the Squared Distance）

DTW和ED都需要开方计算（square root calculation）。由于平方根距离和平方距离均是单调凸函数（monotonic and concave），因此采用平方距离计算时，并不会改变最近邻的相对排序（the relative rankings of nearest neighbors）；此外，相比平方根距离，平方距离更易于优化（the absence of the square root function will make later optimizations possible and easier to explain）。

4.1.2 下界距离（Lower Bounding）

利用计算时间复杂度低的下界距离对候选子序列进行过滤（A classic trick to speed up sequential search with an expensive distance measure such as DTW is to use a cheap-to-compute lower bound to prune off npromising candidates）。

$\text{LB}_{\text{Kim}}FL$下界距离（ $\mathcal{O} (1)$）：采用 $C$和 $Q$的第一（最后）点对间的距离作为下界距离（原始 $\text{LB}_{\text{Kim}}$需要计算两个时间序列间距的最大值和最小值（the original definition of $\text{LB}_{\text{Kim}}$ also uses the distances between the maximum values from both time series and the minimum values between both time series in the lower bound），其计算时间复杂度为 $\mathcal{O} (n)$），然而经标准化后，这两个极值变得很小。忽略这两个极值后，计算时间复杂度为 $\mathcal{O} (1)$）；

$\text{LB}_{\text{Keogh}}$下界距离（ $\mathcal{O} (n)$）：首先构造 $Q$的上边界 $U$和下边界 $L$，然后分别计算 $U$、 $L$与 $C$对应各点对间的距离，取二者中较小的作为距离下界。

4.1.3 提前终止ED和Keogh下界距离计算（Early Abandoning of ED and $\text{LB}_{\text{Keogh}}$）

计算ED、 $\text{LB}_{\text{Keogh}}$下界距离时，当累积的差值平方和（the current sum of the squared
differences）大于 $\text{best-so-far}$时，终止计算。

4.1.4 提前终止DTW距离计算（Early Abandoning of DTW）

已知 $\text{LB}_{\text{Keogh}}$上下边界，计算DTW第 $K$个路径点时， $\text{DTW}(Q_{1 : K}, C_{1 : K} + \text{LB}_{\text{Keogh}}(Q_{K + 1 : n}, C_{K + 1 : n}))$为真实DTW距离（ $\text{DTW}(Q_{1 : n}, C_{1 : n})$）的下界，即

$\text{DTW}(Q_{1 : K}, C_{1 : K} + \text{LB}_{\text{Keogh}}(Q_{K + 1 : n}, C_{K + 1 : n})) \leq \text{DTW}(Q_{1 : n}, C_{1 : n})$

当该下界大于 $\text{best-so-far}$时，终止计算（compute the DTW from $1$ to $K$, sum the partial DTW accumulation with the $\text{LB}_{\text{Keogh}}$ contribution from $K + 1$ to $n$，This sum of $\text{DTW}(Q_{1 : K}, C_{1 : K} + \text{LB}_{\text{Keogh}}(Q_{K + 1 : n}, C_{K + 1 : n}))$ is a lower bound to the true DTW distance ( $\text{DTW}(Q_{1 : n}, C_{1 : n})$)，If at any time this lower bound exceeds the best-so-far distance we can admissibly stop the calculation and prune this $C$）。

4.1.5 多核处理（Exploiting Multicores）

4.2 UCR优化策略（Novel Optimizations: The UCR Suite）

本文给出4种基于ED和DTW距离的优化策略。

4.2.1 提前终止标准化（Early Abandoning Z-Normalization）

本文将提前终止ED（或Keogh下界距离）计算与在线（online）标准化（Z-Normalization）结合。子序列的均值和方差可通过更新两个相差 $m$个值的（a lag of exactly $m$ values）求和（keeping two running sums）计算：

$\mu = \frac{1}{m} \left( \sum_{i = 1}^{k} x_{i} - \sum_{i = 1}^{k - m} x_{i} \right), \quad \sigma^{2} = \frac{1}{m} \left( \sum_{i = 1}^{k} x_{i}^{2} - \sum_{i = 1}^{k - m} x_{i} ^{2}\right) - \mu^{2}$

为避免累积浮点误差（accumulation of the floating-point error），每一百万条子序列执行一次完全标准化（once every one million subsequences, we force a complete Z-normalization to “flush out” any accumulated error）。

4.2.2 重排序提前终止（Reordering Early Abandoning）

排序的差异对加速产生的影响很大（on a query-by-query basis, different orderings produce different speedups）

本文猜测：基于标准化 $Q$的绝对值对索引排序是通用最优顺序（the universal optimal ordering is to sort the indices based on the absolute values of the Z-normalized $Q$）。标准化候选子序列搜索问题中， $C_{i}$大多服从0均值高斯分布，因此查询序列中绝对值最大的部分对距离度量的平均贡献最大（for subsequence search, with Z-normalized candidates, the distribution of many $C_{i}$’s will be Gaussian, with a mean of zero. Thus, the sections of the query that are farthest from the mean, zero, will on average have the largest contributions to the distance measure）。该技巧可应用于ED和 $\text{LB}_{\text{Keogh}}$（use this trick for both ED and $\text{LB}_{\text{Keogh}}$），并与提前终止标准化（4.2.1）一起使用（use it in conjunction with the early abandoning Z-normalization technique）。

4.2.3 交换查询序列与候选序列在 $\text{LB}_{\text{Keogh}}$中的角色（Reversing the Query/Data Role in $\text{LB}_{\text{Keogh}}$）

通常， $\text{LB}_{\text{Keogh}}$下界距离为查询序列构造包络（normally the $\text{LB}_{\text{Keogh}}$ lower bound builds the envelope around the query），记为 $\text{LB}_{\text{Keogh}}\text{EQ}$。由于 $\text{LB}_{\text{Keogh}}\text{EQ}$只需计算一次，因此节省时间和空间开销（save the time and space overhead）。

本文为每个候选序列构造包络，记为 $\text{LB}_{\text{Keogh}}\text{EC}$。

仅当其余下界无法剪枝时，才计算 $\text{LB}_{\text{Keogh}}\text{EC}$（selectively calculate $\text{LB}_{\text{Keogh}}\text{EC}$ in a “just-in-time” fashion, only if all other lower bounds fail to prune），因此消除了空间开销（remove space overhead）。

时间开销能够通过减少DTW计算获得补偿（the time overhead pays for itself by pruning more full DTW calculations）。

注意： $\text{LB}_{\text{Keogh}}\text{EQ} \neq \text{LB}_{\text{Keogh}}\text{EC}$

4.2.4 级联多个下界（Cascading Lower Bounds）

下界需在紧致性与计算复杂度之间妥协（a tradeoff between the tightness of the lower bound and how fast it is to compute）。

下界紧致性衡量： $\frac{\text{LB}(A, B)}{\text{DTW}(A, B)}$

选择天际线（skyline）上的下界（Fig. 9中的虚线）。注意提前终止DTW计算（4.1.4）不在Fig. 9中，该方法逐步累加DTW并与下界比较，直至得到最终结果（it produces a spectrum of bounds, as at every stage of computation it is incrementally computing the DTW until the last computation gives the final true DTW distance）。

本文将天际线上的各下界级联使用（use all of the lower bounds on the skyline in a cascade）：

（1）计算 $\text{LB}_{\text{Kim}}FL$， $\mathcal{O} (1)$，剪枝；

（2）计算 $\text{LB}_{\text{Keogh}EQ}$（ $\mathcal{O} (n)$），剪枝；

（3）计算 $\text{LB}_{\text{Keogh}EC}$（4.2.3），剪枝；

（4）计算DTW（4.1.4，提前终止）

在大规模搜索问题中，上述方法可减少99.9999%的DTW计算（prune more than 99.9999% of DTW calculations for a large-scale search）。

5 实验

5.1 随机游走基线测试（Baseline Tests on Random Walk）

5.2 长序列查询：脑电图（Supporting Long Queries: EEG）

5.3 超长序列查询：脱氧核糖核酸（Supporting Very Long Queries: DNA）

5.4 实时数据（Realtime Medical and Gesture Data）

5.5 加速现有挖掘算法（Speeding up Existing Mining Algorithms）

6 结论