【图机器学习】cs224w Lecture 10 - PageRank

PageRank
- Problems
Personalized PageRank

转自本人：https://blog.csdn.net/New2World/article/details/106233258

将互联网视为图的话，它必定存在结构上的一些规律。首先回顾一下强连通子图 (strongly connected component, SCC)，如果一个有向图的子图内任意节点可以互相到达，那么这就是一个 SCC。而包含节点 A 的 SCC 必满足 \(SCC(A)=Out(A)\cap In(A)\) 其中 Out 和 In 分别表示从 A 出发能到达的点以及能到达 A 的点。
在 2000 年的一篇互联网分析论文中显示，当时互联网节点大概 2 千万左右，链接数在 15 亿上下。对于随机点的 Out 和 In 大概都覆盖了半个互联网，即 1 千万个点，由这个随机点得到的 SCC 覆盖了 1/4 个互联网。由此我们可以大致画出互联网的构成关系图。

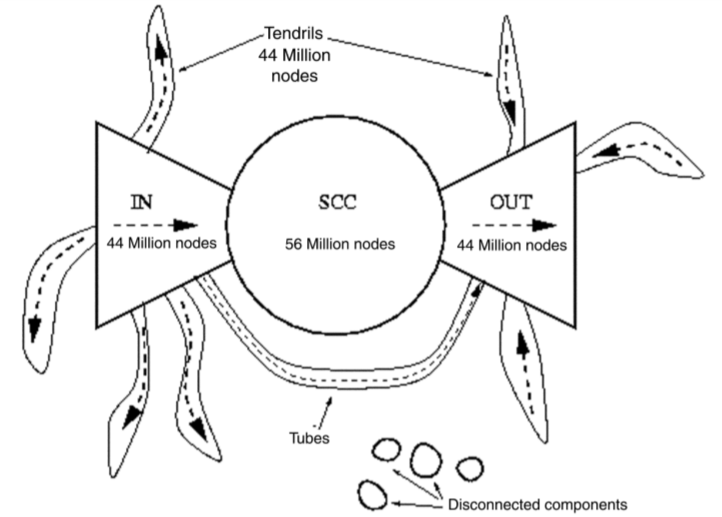
SCC structure

PageRank

搜索引擎的工作就是根据我们提供的关键词对如此大规模的网页进行相关性排序的过程，然后将最相关的多条链接返回给用户。然而互联网如此之大，我们提供的关键词并不精确，当同时存在多条完美匹配的记录时怎样尽可能返回更优质的链接成为了曾经的一道难题。当时在 Stanford 就读的 Google 创始人之一 Larry Page 和他的小伙伴提出了 PageRank —— 一种网页评分的迭代策略。因此 PageRank 中的 Page 实际上是人名。
PageRank 的思想很简单，把网页间的链接视为一种均匀的投票机制。比如节点 v 有三个外链，且其自身的初始“票权”为 1。那么迭代开始后，v 会将自己的票平分给三个外链，即每个外链能得到 1/3。同理如果 v 是其它节点的外链，那 v 也会得到其它节点平分后的票。一直这么迭代下去直到收敛就是 PageRank 的核心过程。或者另一种解释是通过 random walk 来理解。如果当前我们位于节点 v，那么我们可以等概率的转移到 v 指向的所有邻接节点。当转移足够多次后会达到一个类似 MDP 中的稳定状态，表示在任意时间点我们位于各个节点的概率。
Talk is cheap, show me the 'math'. \(r\) 为权重，\(d\) 为出度。

\[r_j = \sum_{i\rightarrow j}\frac{r_i}{d_i} \]

写成矩阵的形式为 \(r = M \cdot r\)，其中 \(M_{ij}\) 表示 j 到 i 的权重，也就是说 \(M\) 的每一行其实是入度，这与邻接矩阵恰好相反。
回过头看看这个矩阵表示 \(r = M\cdot r\)，是不是很像特征值的定义？也就是说，当满足 \(r = M\cdot r\) 时，\(r\) 是 \(M\) 的(主)特征向量，且对应的特征值为 1，而这个 \(r\) 就是一个 stationary 的权重分布。
虽然这个问题看似可以通过解线性方程组的方式得到解析解，然而这样做忽略了一个重要的前提：网络的规模。要解决一个有千万甚至上亿个变量的方程组，时间开销不是玩笑……

Power iteration

初始化：\(r\)
迭代：\(r^{(t+1)}=M\cdot r^{(t)}\)
停止：\(|r^{(t+1)}-r^{(t)}|_1<\epsilon\)

Problems

目前为止 PageRank 很完美，然而它遇到两种情况时会出现 bug。

Dead ends：没有 out-link 的节点，这种节点会导致整个系统的权重泄漏。(不收敛)
Spider traps：对于一个节点群，所有的 out-links 都指向群体内部节点。这种情况会导致这个节点群吸收掉整个系统中的所有权重。(收敛得到的结果并非我们想要的)

上述两个问题可由随机跳转方法解决

遇到 dead ends 时以概率 1 跳转到其它任意节点。
系统判断进入 trap 后，以概率 p 转移到其它任意节点。

而 Google 将这随机跳转和 PageRank 统一起来，通过设定概率 \(\beta\) 来控制迭代过程。以 \(\beta\) 的概率规规矩矩地迭代；以概率 \(1-\beta\) 的概率跳转到任意节点。

\[r_j = \sum_{i\rightarrow j}\beta\frac{r_i}{d_i}+(1-\beta)\frac1N \]

通常来说 \(\beta=0.8\ 0.9\)，即平均 5 次迭代后跳转。不过这么做的前提是 dead ends 已经被提前处理掉了，比如直接删除 dead ends，或在 dead ends 处以概率 1 进行跳转。在实际运算中，并不会将 \((1-\beta)/N\) 直接加到矩阵里去。因为加上 \((1-\beta)/N\) 后会破坏 \(M\) 稀疏矩阵的性质，这样会耗费大量存储空间。因此一般先计算 \(\beta M\cdot r\) 然后对得到的 \(r\) 向量的每一项加上 \((1-\beta)/N\)。
下面给出 PageRank 的伪码

PageRank pseudocode

没有 dead ends 的情况下，系统不会出现权重泄漏的情况。一旦出现 dead end，权重泄漏会导致 \(\sum_jr_j^{new}<1\)，因此上面的伪码中通过记录权重和 S 来弥补泄漏。而这里必定有 \((1-S)/N \geq (1-\beta)/N\)

Personalized PageRank

现在考虑另一个问题，计算机领域如此多大大小小的会议以及投各个会议的大牛们，如何通过各研究者投的会议来推断哪些会议涉及的领域相似。

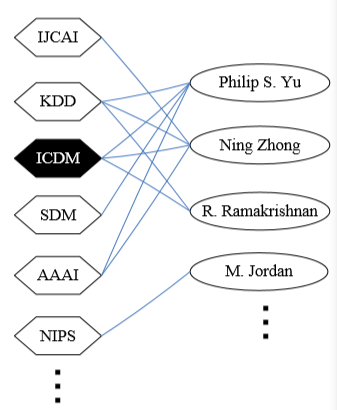
conference

其实这个问题也是一个相关性排序的问题，只不过出发点固定为了你想查询的那个会议。还是通过 random walk 的思想来解决。比如要查询 ICDM，那从 ICDM 出发能通过 Philip S. Yu 到达 KDD, SDM 和 AAAI，通过 Ning Zhong 到达 IJCAI。问题是如果“走到头”了怎么办？这里就不能随机跳了，因为很有可能会跳到毫不相关的会上去。因此这里使用的是 random walk with restart，顾名思义走不动了就回到起点，即 ICDM 然后重新开始。就这样不停的 random walk 就能得到到达各个会议的次数，根据次数排序就是相关度排序了。而且这种方法能同时查询多个会议。

总结一下，PageRank 实质其实就是一个 random walk 的过程，而几种不同的 PageRank 的区别仅在于跳转后落点的概率 S。

PageRank：\(S=[1/N, 1/N, 1/N,..., 1/N]\)
Personalized：\(S=[0.1, 0, 0.1,..., 0.2, 0,..., 0.3]\) (反正和为 1)
Random Walk with Restart：\(S=[0, 0, 0, 1, 0,..., 0]\)