傅里叶变换是电子信息类专业的核心课程,是很多大学生的噩梦课程,傅里叶变换的思想是现代电信科技的数学基础,贯穿了信号处理、运动控制、图像处理、电路分析以及光学等众多领域。如此重要的数学理论思想,无论是学生还是从事技术工作的人都有必要深刻领会。写此文的目的一是基于自己当年没有学懂,工作后回过头来再看,有种恍然大悟的感觉,二是找个地方做个笔记,方便以后查看学习。
程序演示
再次重新学习傅里叶变换是基于斯坦福大学的EE261课程-The Fourier Transforms and its Applications,最初是在网易公开课看到的视频,后来不知道为什么网易撤掉了此课程,再后来又从youtube重新看了一遍。现在有油管工已经把视频搬到了B站。配套的pdf文档可以在CSDN下载频道搜索下载。
欧拉在研究绳子的波动现象时,最早就提出绳子的波动形态可以分解成两个甚至更多的正弦波的叠加。
假如有三个正弦函数,分别为 s i n 2 π t sin2\pi t sin2πt、 s i n 4 π t sin4\pi t sin4πt、 s i n 6 π t sin6\pi t sin6πt,假设幅值都为1,他们的函数图像如下所示。
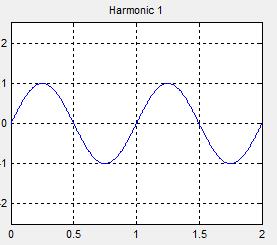
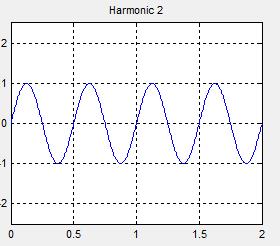
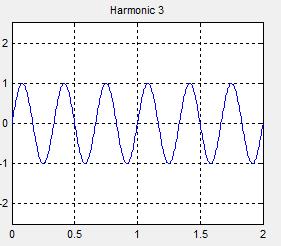
把这三个函数相加会得到什么呢 ?

从上图我们可以看到,不同频率的正弦函数相加后,仍然得到一个周期函数,此时周期为1。从这里我们可以得到波动叠加的第一个重要思想:多个频率,一个周期,叠加后的周期为最长的那个正弦周期。意思是叠加后的周期函数包含多个频率成分,但周期只有一个,等于分解后正弦分量的最长周期。
此处分享一个EE261课程中老师分享的一个波形合成Matlab程序,下载地址:sinsum2.zip
下载文件后解压缩,然后用matlab打开.m文件,运行后出现如下界面。

最上面是输入正弦函数的个数,第二行逐个选择每个函数后,在第三行里设置幅度和相位,配置后即可自动显示叠加效果。
理论计算
傅里叶在前人思路的基础上大胆设想,任意周期函数都可以分解成若干个三角函数的叠加,该思想写在一片论文中提交给了法国科学院,遗憾的是当时的科学院权威拉普拉斯觉得这个理论不够严谨,没有同意论文的发表。当然这并没有阻碍这种思想后来在工程领域大放异彩,特别是通信领域,把信号进行傅里叶级数分解后,把不需要频率成分去除,即可达到滤波的作用,当然这是后话。
三角函数 s i n 2 π t sin2\pi t sin2πt ,其周期 T = 1,即 s i n 2 π ( t + 1 ) = s i n 2 π t sin2\pi(t+1) = sin2\pi t sin2π(t+1)=sin2πt
对于任意的周期为1的函数,可以表达为N个正弦函数的和, f ( t ) = ∑ k = 1 N A k s i n ( 2 π k t + ϕ k ) f(t) = \sum_{k=1}^N A_k sin(2\pi kt + \phi_k) f(t)=k=1∑NAksin(2πkt+ϕk)
将正弦函数展开后得到 f ( t ) = ∑ k = 1 N A k ( s i n 2 π k t c o s ϕ k + c o s 2 π k t s i n ϕ k ) f(t) = \sum_{k=1}^N A_k (sin2\pi kt \; cos \phi_k \; + \; cos2\pi kt \; sin \phi_k ) f(t)=k=1∑NAk(sin2πktcosϕk+cos2πktsinϕk)
对于一个函数,初始相位是常数,即 c o s ϕ k , s i n ϕ k cos \phi_k, sin \phi_k cosϕk,sinϕk为常数,继续化简上面的表达式: f ( t ) = ∑ k = 1 N ( a k c o s 2 π k t + b k s i n 2 π k t ) f(t) = \sum_{k=1}^N (a_k \; cos2\pi kt \; \; + \; b_k \; sin2\pi kt \; ) f(t)=k=1∑N(akcos2πkt+bksin2πkt)
如果在 f ( t ) f(t) f(t)含有直流分量(常数项)的情况下,表达式
可以写为 f ( t ) = a 0 2 + ∑ k = 1 N ( a k c o s 2 π k t + b k s i n 2 π k t ) \boxed{f(t) =\; \frac{a_0}{2} \; + \sum_{k=1}^N (a_k \; cos2\pi kt \; \; + \; b_k \; sin2\pi kt \; ) \quad \quad} f(t)=2a0+k=1∑N(akcos2πkt+bksin2πkt)
此即为傅里叶级数的三角表达式。
圆周运动的虚指数表达
国内的课程在三角函数的基础上会继续展开推导其它内容,比如系数 a k 、 b k a_k、b_k ak、bk,三角函数在计算的时候非常的繁杂,在进行积分、微分的时候也不便捷。想当年高中的时候,最头疼的就是三角函数部分的学习,现在回过头来看,我们当年的课程引入三角函的视角就是错误的,不应该由三角形引入三角函数,而是应该从圆周运动入手。
在继续下面的文章之前,有必要理清一个思路:圆周运动中,半径在坐标轴上的投影,即为三角函数。
θ \theta θ 可以表示为 ω t \omega t ωt

后来理论学家们把傅里叶级数三角函数的表达式改写成了虚指数形式,当然,这个伟大的创举首先要感谢欧拉!虚指数表达中,把笛卡尔坐标的y轴改为虚轴i。我们用 e i ω t e^{i\omega t} eiωt 来表示一个半径为单位长度1的圆,圆周上一点A以角频率 ω \omega ω,做逆时针旋转。同样,可以用 e − i ω t e^{-i\omega t} e−iωt来表示顺时针旋转。
在某一时刻,A转过的角度 θ = ω t \theta \; =\; \omega t θ=ωt。可以得到下列关系式,建立起了虚指数与三角函数的关系。
e i θ = c o s θ + i s i n θ e^{i\theta}\;=\; cos\theta\;+\; isin\theta eiθ=cosθ+isinθ
e − i θ = c o s ( − θ ) + i s i n ( − θ ) = c o s θ − i s i n θ e^{-i\theta} ={}cos(-\theta)+ isin(-\theta) {} \\ =\; cos\theta\;-\; isin\theta e−iθ=cos(−θ)+isin(−θ)=cosθ−isinθ

下图表示: c o s θ = e i θ + e − i θ 2 cos\theta\;=\; \dfrac{e^{i\theta}+e^{-i\theta}}{2} cosθ=2eiθ+e−iθ

下图表示: s i n θ = e i θ − e − i θ 2 i sin\theta\;=\; \dfrac{e^{i\theta}-e^{-i\theta}}{2i} sinθ=2ieiθ−e−iθ

傅里叶级数的虚指数表达
上面一节我们得到了虚指数和三角函数的关系式,现在可以利用sin和cos的表达式把三角形式的傅里叶级数改写为虚指数形式。
a k c o s 2 π k t + b k s i n 2 π k t = a k e 2 π i k t + e − 2 π i k t 2 + b k e 2 π i k t − e − 2 π i k t 2 i = a k 2 ( e 2 π i k t + e − 2 π i k t ) + b k 2 i ( e 2 π i k t + e − 2 π i k t ) = a k − b k i 2 e 2 π i k t + a k + b k i 2 e − 2 π i k t = ∑ k = − ∞ ∞ C k e 2 π i k t a_k \; cos2\pi kt \; \; + \; b_k \; sin2\pi kt \; = \;a_k \frac{e^{2\pi ikt}+e^{-2\pi ikt}}{2}+b_k \frac{e^{2\pi ikt}-e^{-2\pi ikt}}{2i} \\ = \; \frac{a_k}{2} (e^{2\pi ikt}+e^{-2\pi ikt})\;+\; \frac{b_k}{2i} (e^{2\pi ikt}+e^{-2\pi ikt})\\ = \; \frac{a_k-b_ki}{2} e^{2\pi ikt}+\frac{a_k+b_ki}{2} e^{-2\pi ikt} \\ = \sum_{k=-\infin}^\infin C_k e^{2\pi ikt} akcos2πkt+bksin2πkt=ak2e2πikt+e−2πikt+bk2ie2πikt−e−2πikt=2ak(e2πikt+e−2πikt)+2ibk(e2πikt+e−2πikt)=2ak−bkie2πikt+2ak+bkie−2πikt=k=−∞∑∞Cke2πikt
其中 C k = a k + b k i 2 C_k=\dfrac{a_k+b_ki}{2} Ck=2ak+bki
从上面的推导过程可以看出, C k C_k Ck为共轭复数,满足 C − k = C k ‾ C_-k=\overline{C_k} C−k=Ck。
我们设当 k = 0 k=0 k=0时, C 0 = a 0 2 C_0 =\dfrac{a_0}{2} C0=2a0,从而得到了周期函数 f ( t ) f(t) f(t)的虚指数表达式:
f ( t ) = ∑ k = − ∞ ∞ C k e 2 π i k t \boxed{f(t) =\; \sum_{k=-\infin}^\infin C_k \; e^{2\pi ikt} \; \quad \quad} f(t)=k=−∞∑∞Cke2πikt
说明:
在虚指数表达式里出现了负频率,此处负频率并没有实际的物理意义,从上面的推导过程我们可以知道,负频率只是为了让最终的计算结果为实数。
上面公式的推导都是以周期为1进行的,如果对于任意周期的傅里叶系数将会在后续章节中提及。依据的公式无非是 ω = 2 π T \omega=\dfrac{2\pi}{T} ω=T2π, c o s θ = c o s ω t = c o s 2 π T t cos\theta=cos\omega t =cos\frac{2\pi}{T}t cosθ=cosωt=cosT2πt。
下篇博文会提到向量空间,正交基,映射,内积等概念,推导出傅里叶系数 C k C_k Ck的表示方法。