线性回归可以用以下式子进行描述：
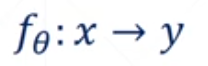
线性回归即连续值的预测问题，即根据给定的x以及模型参数θ的计算下，使得该方程的相应能够无限逼近真实值y。
下面来举一个连续值预测的简单例子：
y = w * x + b
当知道两组参数时，即可通过消元法求得参数w与b，即可得到该方程的精确解。即w = 1.477， b = 0.089
1.567 = w * 1 + b
3.043 = w * 2 + b
但是现实生活中往往不能够精确求解，首先因为模型本身的方程是未知的，采集的数据都是带有一定偏差的，其次我们观测到的数据往往是带有一定噪声的。因此需要在上面式子中增加一个噪声因子ε,即
y = w * x + b + ε，我们假设ε~N(0，1) ，即 ε服从均值为0，方差为1的高斯分布，上述分布如下图所示：
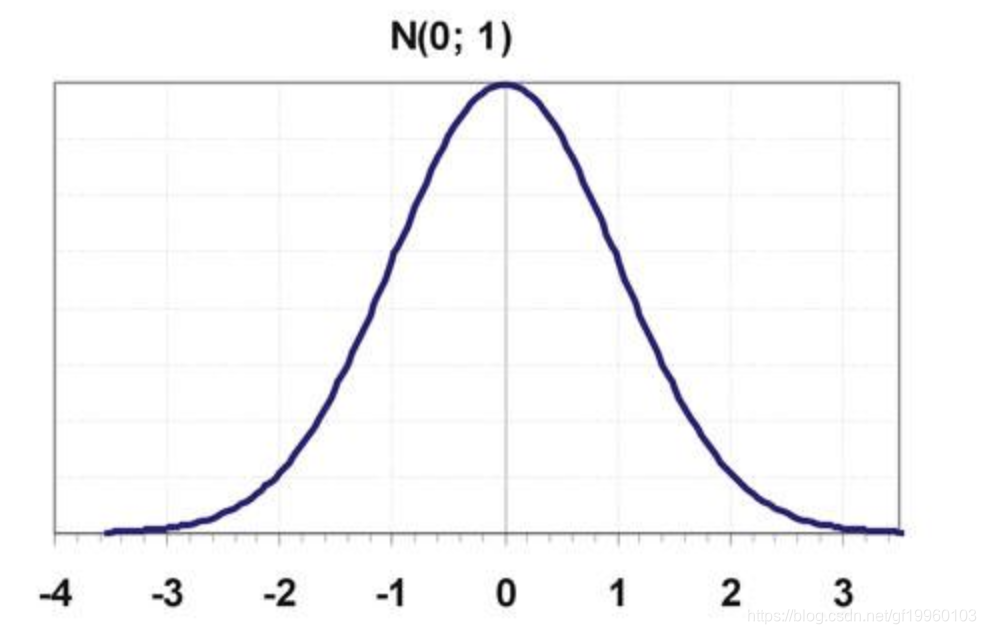
即绝大部分数值都分布在0的附近，离0较远的数值分布较少。
通过高斯分布，上述求解过程可变为：
1.567 = w * 1 + b + eps
3.043 = w * 2 + b + eps
4.519 = w * 3 + b + eps
当我们想要得到合适的w与b的值时，需要多观测几组数据，通过多组观测数据的迭代，获得综合性能最优的w与b。
那么，我们如何求解w和b两个参数呢？
这里，需要引进一个损失函数的概念，即真实值与预测值之间的误差，损失函数公式如下所示：
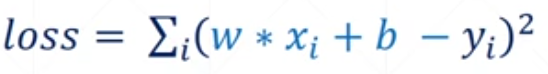
要想获得性能最优的w与b，即在满足损失函数达到最小值这个条件下的w与b，这里的损失函数为每组观测值误差的求和。
所以，我们已经将模型参数w与b参数估计的问题转化为最小化损失函数的问题。
接下来，我们使用梯度下降算法来实现模型参数w与b的确定。在此处不多解释到底什么是梯度下降算法，梯度可以简单理解为函数的导数，梯度的方向即使得函数值增大的方向。例如：
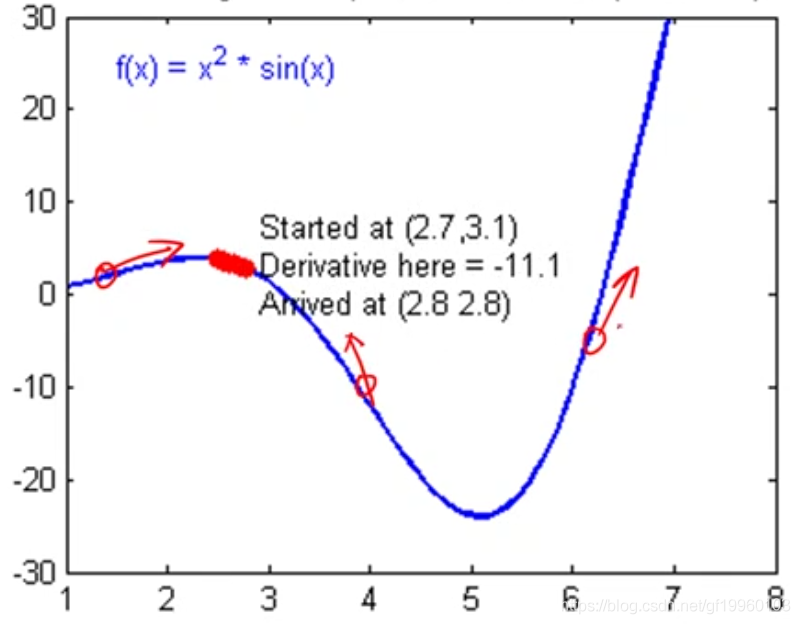
比如目标函数为f(x)，函数在上述三个点导数的方向指向函数值增大的方向，也可以理解为函数极大值的方向，当我们想最小化损失函数时，即求解损失函数的最小值，并获得对应点的w与b，即我们想要获得的模型参数。在上图中，损失函数最小值大概在5的附近，让模型参数验证梯度的反方向进行异动，每次异动固定的步长，即learning rate，通过不断地反复迭代，找到最优的模型参数。
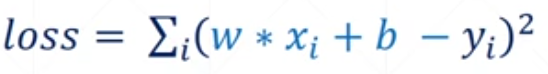
所以，我们需要对目标函数进行求偏导数，即分别计算w'与b'
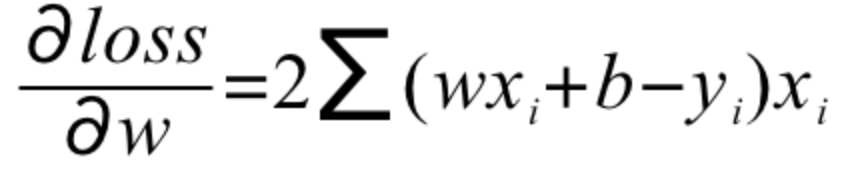
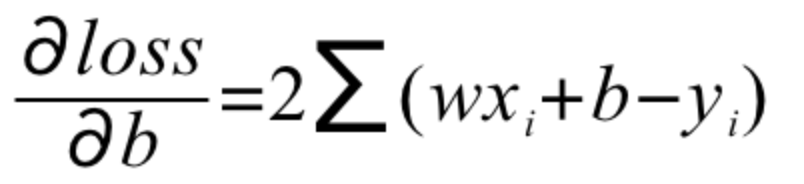
并按照如下方式进行梯度的更新
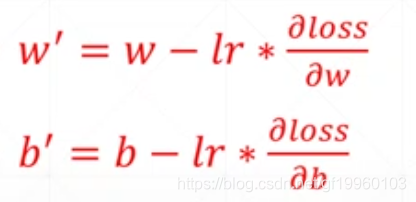
Python代码推导：
#!/usr/bin/env python
# -*- coding: utf-8 -*-
__author__ = 'Seven'
import numpy as np
# y = wx + b
def calculate_loss_function(w, b, points):
total_error = 0
for i in range(len(points)):
x = points[i, 0]
y = points[i, 1]
total_error += ((w * x + b) - y) ** 2
return total_error / float(len(points))
def step_gradient(w_current, b_current, points, learning_rate):
w_gradient = 0
b_gradient = 0
N = float(len(points))
for i in range(len(points)):
x = points[i, 0]
y = points[i, 1]
# w_gradient = 2x(wx+b-y)
w_gradient += 2 / N * x * ((w_current * x + b_current) - y)
# b_gradient = 2(wx+b-y)
b_gradient += 2 / N * ((w_current * x + b_current) - y)
new_w = w_current - learning_rate * w_gradient
new_b = b_current - learning_rate * b_gradient
return [new_w, new_b]
def gradient_descent_runner(starting_w, starting_b, learning_rate, num_iterations, points):
w = starting_w
b = starting_b
for i in range(num_iterations):
w, b = step_gradient(w, b, points, learning_rate)
return [w, b]
def run():
# 构建模拟数据并添加噪声，并拟合y = 1.477x + 0.089
x = np.random.uniform(0, 100, 100)
y = 1.477 * x + 0.089 + np.random.normal(0, 1, 1)
points = np.array([[i, j] for i, j in zip(x, y)])
learning_rate = 0.0001
initial_b = 0
initial_w = 0
num_iterations = 1000
print(f'原始损失函数值为:{calculate_loss_function(initial_w, initial_b, points)}, w={initial_w}, b={initial_b}')
w, b = gradient_descent_runner(initial_w, initial_b, learning_rate, num_iterations, points)
print(f'经过{num_iterations}次迭代, 损失函数的值为:{calculate_loss_function(w, b, points)}, w={w}, b={b}')
if __name__ == '__main__':
run()
运行效果如下：
从上图可以看出，经过1000次迭代w的值约为1.49，b的值约为0.08，真实的w为1.477，b为0.089，运行效果与真实值已经非常接近了。