1
优美的高斯分布



[P29]图1.16很好的描绘了这样表达的优美之处:
2
极大似然估计的病态拟合

3
参数-Regularizer


4
先验分布:高斯分布
高斯分布应该算是我们认知中,描绘一切连续型数值不确定性的最基本、最硬派的先验知识了。
甭管你是什么妖魔鬼怪,只要你是连续的,不是离散的,先给你套个高斯分布的罪状。
当然,钦定高斯分布从数学角度是由原因的,和其优美的数学共轭形式有关。
[P98]的练习证明了,高斯似然分布 x 高斯先验分布,结果仍然是一个高斯分布。
(此证明需要熟读第二章关于高斯分布的 150 个公式,需要很好的概率论、线代基础。)
高斯分布在数学形式上有许多便利,比如下面提到的零均值简化版高斯分布,这为贝叶斯方法招来很多
恶评,[P23] 是这样解释的:贝叶斯方法广受批判的原因之一,是因为其在选取先验概率分布上,根据的是
数学形式的便利为基础而不是 先验分布的信度 。
贝叶斯方法讲究推导严谨,公式齐全,对于那些奇怪的、无法用数学语言表达原理的、广布自然界的先验知识,
如Deep Learning思想,自然不会考虑,这也是为什么有人会认为Deep Learning与Bayesian是对着干的。[Quroa]
5
波动性惩罚:简化高斯分布




6
稀疏性惩罚:L1 Regularizer


I、大脑中有1000亿以上的神经元,但是同时只有1%~4%激活,而且每次激活的区域都不一样。
这是生物神经中的稀疏性。
II、稀疏性将原本信息缠绕密集数据给稀疏化,得到稀疏特征表达。比如将实数5,稀疏为一个[1,0,1]向量,
很容易线性可分了。又比如识别一直鸟,只要把噪声给稀疏掉,保留关键部位,最后就有更好的特征表达。
这是特征表达上的稀疏性,实际应用有[稀疏编码][深度神经网络],当然还有我们的生物神经网络。
当然,以上和L1 Regularizer毫无关系,因为它稀疏的姿势错了,要不然还要Deep Learning作甚。
首先,这个稀疏策略没有Adaptive性,它并不会智能地的发现哪里需要稀疏,哪里不需要稀疏。
从数学规划问题角度理解,它就是一个多元的约束条件,至于哪个元倒霉到被约束至0,这个没人能确定。
其次,参数W直接影响着模型拟合能力,对它错误地稀疏0化,会造成严重的欠拟合。
基于以上两点,不能认为L1与L2类似,就认为L1也能缓解过拟合,实际上它更有可能造成欠拟合。
7
L1&L2 Regularizer图形化理解
来自[P146]、[P107].CHS.HIT.马春鹏的有趣配图,似乎能解释为什么L1会直接得到0,而L2却是无限接近0。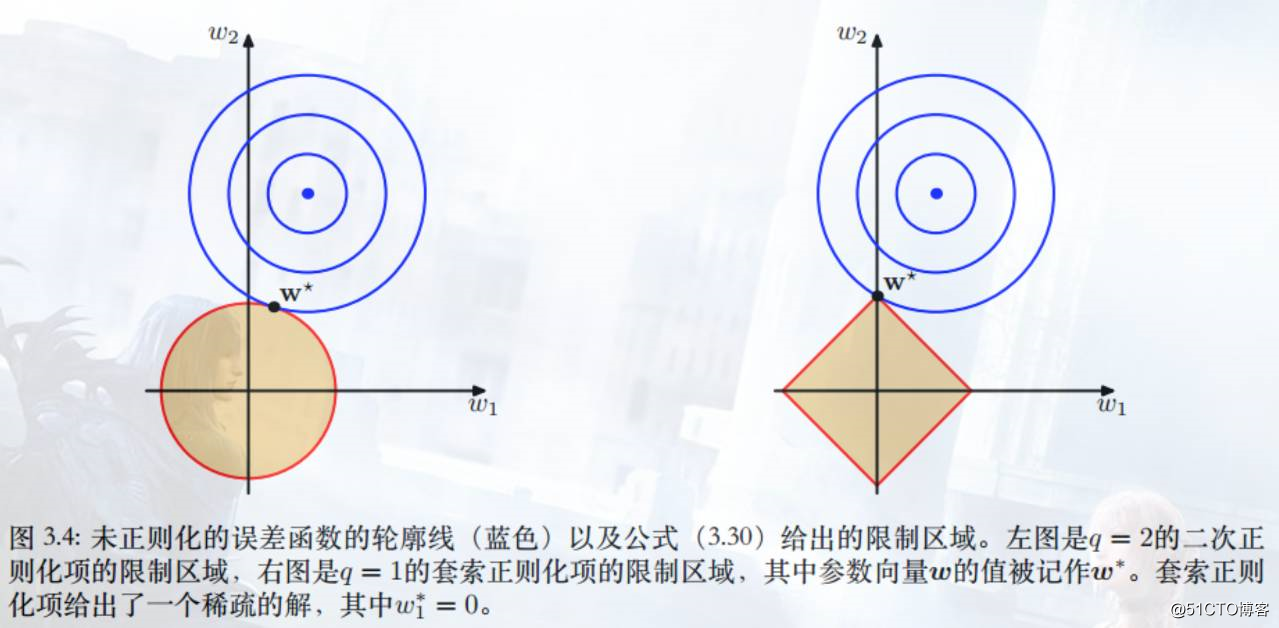
8
更好地发现特征:Adaptive Represention Regularizer
Hinton组的[Erhan10] 认为Deep Learning的Pre-Training也是一个Regularizer,原因有二:
其一,预训练后参数W的搜索方向,有更大可能从局部最小值中逃逸。
其二,预训练后参数W的搜索方向,让似然函数值变大,但是得到了更好的归纳能力(测试错误率变低)。
第一点是比较神奇的Regularizer效果,即使是身披图灵奖的Bayesian方法,也是无法解释的。
第二点有点像是L2 Regularizer的效果,但是更大可能是与模型内部存有的Attention机制有关。
若是固定Pre-Training之后的参数W,那么Pre-Training等效于一个非线性的PCA,预先注入了
对无标签观测数据的先验知识,即得到了更合理的P(W),这又是Bayesian方法所无法解释的。
9
可靠的稀疏性:Adaptive Sparsity Regularizer
Deep Learning中有两个能够自适应引入稀疏性的方法,[ReLU]&[Dropout]。
I、[ReLU]对神经元的输出稀疏,而神经元的输出显然是可变的。
II、[Dropout]是对神经元的输出稀疏,不过方式有点特别,采用随机概率来决定,而不是自适应方法。
但这并不能表明[Dropout]得不到自适应稀疏,它的自适应恰恰来自于随机本身。
由于随机性,每次网络结构都不同,这压迫了参数W朝一个稳定方向调整。
如2.1.2分析,[I]可以认为是发现了稀疏特征,替代L1。[II]可以认为是类似生物神经网络的稀疏激活机制,替代L2。
这两者并不冲突,所以常规Deep Learning模型中,[I]+[II]是标配手段。
博客园:http://www.cnblogs.com/neopenx/p/4820567.html
推荐阅读:
精选干货|近半年干货目录汇总
干货|台湾大学林轩田机器学习基石课程学习笔记5 -- Training versus Testing
干货|MIT线性代数课程精细笔记[第一课]
欢迎关注公众号学习交流~ 
欢迎加入交流群交流学习
