题意:

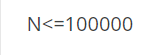
解法:
( X + 1 ) 3 − X 3 = ( X + 1 ) 2 ( X + 1 ) − X 3 = ( X 2 + 2 X + 1 ) ( X + 1 ) − X 3 = X 3 + X 2 + 2 X 2 + 2 X + X + 1 − X 3 = 3 X 2 + 3 X + 1 即 在 X 个 1 之 后 再 增 加 一 个 1 , 总 分 数 会 增 加 3 X 2 + 3 X + 1 令 c n t [ i ] 表 示 i 次 操 作 后 X 的 期 望 值 那 么 c n t [ i ] = ( c n t [ i − 1 ] + 1 ) ∗ p [ i ] + 0 ∗ ( 1 − p [ i ] ) = ( c n t [ i − 1 ] + 1 ) ∗ p [ i ] 令 c n t 2 [ i ] 表 示 i 次 操 作 后 X 2 的 期 望 值 那 么 c n t 2 [ i ] = ( c n t 2 [ i − 1 ] + 2 ∗ c n t [ i − 1 ] + 1 ) ∗ p [ i ] 令 d [ i ] 表 示 i 次 操 作 后 的 期 望 分 数 那 么 d [ i ] = d [ i − 1 ] + ( 3 ∗ c n t 2 [ i − 1 ] 2 + 3 ∗ c n t [ i − 1 ] + 1 ) ∗ p [ i ] . 注 意 : X 的 期 望 值 和 X 2 的 期 望 需 要 分 开 算 . (X+1)^3-X^3\\ =(X+1)^2(X+1)-X^3\\ =(X^2+2X+1)(X+1)-X^3\\ =X^3+X^2+2X^2+2X+X+1-X^3\\ =3X^2+3X+1\\ 即在X个1之后再增加一个1,总分数会增加3X^2+3X+1\\ 令cnt[i]表示i次操作后X的期望值\\ 那么cnt[i]=(cnt[i-1]+1)*p[i]+0*(1-p[i])=(cnt[i-1]+1)*p[i]\\ 令cnt2[i]表示i次操作后X^2的期望值\\ 那么cnt2[i]=(cnt2[i-1]+2*cnt[i-1]+1)*p[i]\\ 令d[i]表示i次操作后的期望分数\\ 那么d[i]=d[i-1]+(3*cnt2[i-1]^2+3*cnt[i-1]+1)*p[i].\\ 注意:X的期望值和X^2的期望需要分开算. (X+1)3−X3=(X+1)2(X+1)−X3=(X2+2X+1)(X+1)−X3=X3+X2+2X2+2X+X+1−X3=3X2+3X+1即在X个1之后再增加一个1,总分数会增加3X2+3X+1令cnt[i]表示i次操作后X的期望值那么cnt[i]=(cnt[i−1]+1)∗p[i]+0∗(1−p[i])=(cnt[i−1]+1)∗p[i]令cnt2[i]表示i次操作后X2的期望值那么cnt2[i]=(cnt2[i−1]+2∗cnt[i−1]+1)∗p[i]令d[i]表示i次操作后的期望分数那么d[i]=d[i−1]+(3∗cnt2[i−1]2+3∗cnt[i−1]+1)∗p[i].注意:X的期望值和X2的期望需要分开算.
code:
#include <bits/stdc++.h>
using namespace std;
const int maxm=1e6+5;
double cnt[maxm];
double cnt2[maxm];
double d[maxm];
double p[maxm];
int n;
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>p[i];
}
for(int i=1;i<=n;i++){
cnt[i]=(cnt[i-1]+1)*p[i];
cnt2[i]=(cnt2[i-1]+2*cnt[i-1]+1)*p[i];
d[i]=d[i-1]+(3*cnt2[i-1]+3*cnt[i-1]+1)*p[i];
}
printf("%.1f\n",d[n]);
return 0;
}