PCA Excel演算
1 声明
本文的数据来自网络,部分代码也有所参照,这里做了注释和延伸,旨在技术交流,如有冒犯之处请联系博主及时处理。
2 PCA简介
主成分分析(Principal Components Analysis),简称PCA,是一种数据降维技术,用于数据预处理。在PCA中,数据从原来的坐标系转化到新的坐标系中。通常第一个新坐标轴选择的是原始数据方差最大的方向,第二个坐标轴是与第一个坐标轴正交且具有最大方差的方向,也即是第二个选取的方向应该和第一个方向具有很弱的相关性。
3 PCA计算过程
假设有如下的二维数据,分别是x、y来演示PCA的计算过程(这里y并不是因变量)。
Step 1:计算连续变量的x、y的均值
| x |
y |
| 2.5 |
2.4 |
| 0.5 |
0.7 |
| 2.2 |
2.9 |
| 1.9 |
2.2 |
| 3.1 |
3.0 |
| 2.3 |
2.7 |
| 2.0 |
1.6 |
| 1.0 |
1.1 |
| 1.5 |
1.6 |
| 1.1 |
0.9 |
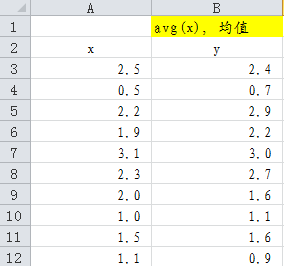
则可以通过excel的AVERAGE函数,如AVERAGE(A3:A12)得到x列的均值。
![]()
Step 2:计算离差(随机变量与其均值的差,去中心化)

注:1 这里以x和y的最后一个元素为例,则离差分别为A12-A13=1.1-1.81=-0.71和B12-B13=0.9-1.91=-1.01.
2 这里的D和E列是标准化后的数据记为dataAdjust,则其为一个10*2的矩阵。
Step 3:计算x和y的协方差
两变量协方差的公式是
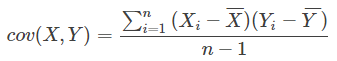
所以这里即转换成:
- x、y对应的离差相乘再求和
- 将1)式除以n-1

这里以最后一列的0.72为例 ,D12*E12=(-0.71)*(-1.01)=0.72
Step 4:构建协方差矩阵
两变量协方差矩阵的一般形式如下:
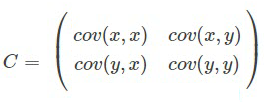
这里的cov(x,x)即是x的方差,cov(x,y)见Step3的结果,即0.615444444。。
其中方差的公式:
![]()
则得到协方差矩阵如下:
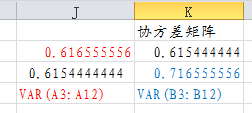
以cov(x,x) x的方差为例,VAR(A3:A12)= 0.616555556
Step 5: 计算特征值并按大小排序
![]() (这里设k为特征值)由上式得,
(这里设k为特征值)由上式得,
(0.616555556-k)*(0.716555556-k)-0.615444444*0.615444444 = 0
整理后得出
k*k-(0.716555556+0.616555556)*k+0.716555556*0.616555556-0.615444444*0.615444444
则按照一元二次方程的标准形式:![]()
a=1
b=-1.333111112
c= 0.063024445584
这里令d= ![]() 则,d=1.525087455
则,d=1.525087455
用excel解出k的两个根。
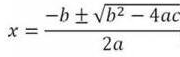
即λ1=0.0490834,λ2= 1.284027712

按照特征值大小排序,这里因为是两个,选择大的λ2。
Step 6: 计算特征向量
将得到特征值分别带入特征方程中,最终得向量分量间的关系为a1=0.92*a2,再通过单位化(a1*a1+a2*a2=1)最终得到特征向量。(非严格演算)
最终的特征向量为:(-0.6778734, -0.73517866)T

或者用python里的scipy求解:
import numpy as np
np.set_printoptions(precision=8)
import numpy as np
from scipy import linalg
A=np.array([[0.616555556,0.615444444],[0.615444444,0.716555556]])
evalue,evector=linalg.eig(A)
print(evalue)
print(evector)

Step 6:得到将维的矩阵
用step2里的dataAdjust矩阵(10*2)乘以特征向量(2*1)最终得到10*1的矩阵。

4 总结
PCA的处理步骤如下:
- 对样本进行去中心化操作。
- 计算样本矩阵的协方差矩阵
- 对协方差矩阵进行特征分解,计算特征值和特征向量
- 特征值从大到小排序
- 保留最上面k个特征向量
- 将数据转换到k个向量构件的新空间中
- n维矩阵*k维特征向量=k维矩阵