前景: 力扣里所谓的简单题并不一定简单,很多的官方解题思路都是很巧妙的。
暂时做个记录

很简单的知识点
bool类型的true转换为整数是1,false转换为整数是0
主要涉及题型:
排序,各种奇怪的排序:
按奇、偶排序: 例如力扣#905题,
利用交换实现排序,结合map等等
查找:
数组、链表等的反转
树相关的问题:
字符串相关的重复、查找等:
最长、最短等一系列经典的动态规划相关的题目:
不同的经典数据结构的拓展和互相模拟:栈模拟队列,队列模拟栈,增加记录最大值功能的栈等等
练题过程中涉及到的一些知识点:
基础的:
STL相关的一系列操作:其中用的最多的就是vector和unordered_map ,stack偶尔也会用到,优先队列(priority_queue)也有用到过,还有一些对字符串string 的操作(可以find,push_back等)
1.对数组和字符串的一些巧妙方法:例如反转左右部分再整体反转等等;
2.vector和map的结合使用:例如利用map中查找元素的时间复杂度为O(1)的特点,用map的空间消耗,换取时间上的优势
3.诸如:字典树这种巧妙的结构,字典树(用来查找字符串,速度甚至比hash还快)
字典树:
又称单词查找树,Trie树,前缀树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来节约存储空间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。
字典树的基本功能是用来查询某个单词(前缀)在所有单词中出现次数的一种数据结构,它的插入和查询复杂度都为O(len),Len为单词(前缀)长度,但是它的空间复杂度却非常高,如果字符集是26个字母,那每个节点的度就有26个,典型的以空间换时间结构。
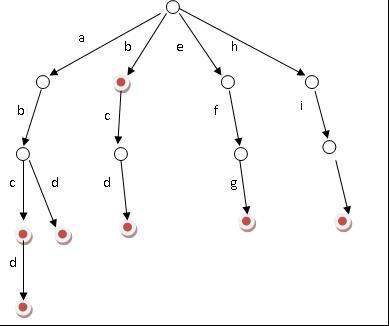
下面我们选的存储字典树节点的数据结构为:
typedef struct node
{
struct node *next[Max]; //表示对于每个节点最多有26个孩子节点
int num; //表示存储的孩子节点的个数
bool flag;//表示当前节点是否为字符串的结尾,或者是字符串的前缀
}Node;
说明:
最常用的有三个操作,插入单词、搜索单词是否在字典树中、搜索前缀是否在字典树中。
插入单词:node指向根节点,从单词的第一个字符开始判断,该字符是否在节点指向的字母映射表中出现(不为nullptr空指针),如果没有出现过就创建对应的内存空间,然后node指向对应字母的链接。重复操作,直到该单词全部插入完,再另最后的尾结点node->flag=true()(表示一个单词的结尾)。有点类似链表的插入。
查找单词是否在字典树中:同样,node先指向根节点,然后从单词的第一个字符开始判断,该字符是否在node指向的字母映射表中出现,如果没有出现直接return false,否则node指向对应字母的链接,重复操作,直至单词全部查询完。最后再判断node->flag == true?,如果不为true,则表示并不是单词的结尾(该单词没有出现在字典树中,只是前缀包含了该单词)。
查找前缀是否出现在字典树中 :跟上面查找单词是一样的,只是最后不用再判断flag。
字典树的典型应用:
1.统计一组字符串中某前缀出现的次数(直接用上面的代码就行)。
2.判断一组字符串中是否有一个字符串是另一个字符串的前缀。
分析:我们只要在结点中添加一个nEndFlag成员变量即可。若nEndFlag == 1,说明该结点字符是某一字符串的结尾(假设为A),若在插入B字符串的过程中经过这一结点,则说明A是B的 前缀;还有一种情况,当要插入最后一个字符c时,却发现p->next[c-'a']为真,则说明该字符串是一个前缀字符串,eg:先插入abcde,再插入abc这种情况。
3. 串排序:给定N个互不相同的仅由一个单词构成的英文名,让你将他们按字典序从小到大输出
用字典树进行排序,采用数组的方式创建字典树,这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可。
实际应用举例:


以上字典树的知识来源于 https://www.cnblogs.com/dlutxm/archive/2011/10/26/2225660.html