多个RGB相机或深度相机之间的对齐，就是不同坐标系的相互转换；
对齐的作用就是把多个坐标系用一个坐标系去描述，一次对齐能减轻后续代码的计算量。
例如：我最近遇到一个：
RGB相机的图像坐标为（u，v），以相机为原点的相机坐标系下该图像点对应坐标为（x,y,z）
其对应齐次公式为下图，其中K、R、T分别表示内参矩阵，旋转矩阵，平移矩阵，s=z，表示尺度
如果是深度相机对齐到RGB相机，那么KRT就是RGB相机的，反之就是深度相机的。
这样，如果只是图像坐标系转换到相机坐标系的情况下，RT为1
即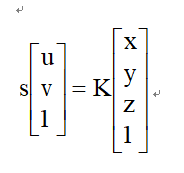
。
如果是深度相机对齐到RGB相机，那么以RGB相机为原点构建坐标系。
假设对(x,y,z)做变换H（如旋转，平移等）得到新的（x2，y2，z2），此时反向计算（x2，y2，z2）对应的（u2，v2）
只需要将
即可。
适用于旋转点云后对原始图像做相应的透视变换的场景。
如果没有对齐的话，还需要考虑深度相机到RGB相机的变换矩阵，会非常麻烦。
需要注意的是，如果涉及平移，可以先计算某个点的平移，再附加到整个图像上
假设平移矩阵为M,那么M*K*H*K_才是平移后的结果。