主要参考书目《统计学习方法》第2版,清华大学出版社
参考书目 Machine Learning in Action, Peter Harrington
用于考研复试笔记,所以写的很简洁,自己能看懂就行。有学习需求请绕道,参考吴恩达机器学习或以上书籍,讲得比大多数博客好。
概念
输入:训练数据集
T = { ( x 1 , y 1 ) , ( x 2 , y x ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),(x_2,y_x),...,(x_N,y_N)\} T={
(x1,y1),(x2,yx),...,(xN,yN)}
其中, x i ∈ χ ⊂ R n x_i \in \chi \subset R_n xi∈χ⊂Rn为实例的特征向量, y i ⊂ Y = { c 1 , c 2 , . . . , c k } y_i\subset Y=\{c_1,c_2,...,c_k\} yi⊂Y={
c1,c2,...,ck}为实例的类别, i = 1 , 2 , . . . , N ; i=1,2,...,N; i=1,2,...,N;实例特征向量 x x x:
输出:实例 x x x所属的类 y y y
(1)根据给定的距离度量,在训练集 T T T中找出与 x x x最邻近的 k k k个点,涵盖这 k k k个点的 x x x的邻域记作 N k ( x ) N_k(x) Nk(x)
(2)在 N k ( x ) N_k(x) Nk(x)中根据分类决策规则(如多数表决)决定 x x x的类别 y y y:
y = arg max c j ∑ x i ∈ N k ( x ) I ( y i = c j ) , i = 1 , 2 , . . . , N ; j = 1 , 2 , . . . , K y=\argmax\limits_{c_j}\sum\limits_{x_i \in N_k(x)}I(y_i=c_j), i = 1,2,...,N;j=1,2,...,K y=cjargmaxxi∈Nk(x)∑I(yi=cj),i=1,2,...,N;j=1,2,...,K
I I I为指示函数,当 y = c j y_=c_j y=cj时 I I I为1,否则 I I I为0.
本质是找距离最近的k个点构成集合,这个集合中最多的种类就是 x x x的种类。
k k k近邻法的特殊情况是 k = 1 k=1 k=1的情形。
k k k近邻没有显式的学习过程。
距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映。 k k k近邻模型的特征空间一般是 n n n维实数向量空间 R n R^n Rn。使用的距离是欧式距离,但也可以是其他距离,如更一般的 L p L_p Lp距离或Minkowski距离。
设特征空间 χ \chi χ是 n n n维实数向量空间 R n R^n Rn, x i , x j ∈ χ , x i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) T , x j = ( x j ( 1 ) , x j ( 2 ) , . . . , x j ( n ) ) T x_i,x_j \in \chi,x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T,x_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)})^T xi,xj∈χ,xi=(xi(1),xi(2),...,xi(n))T,xj=(xj(1),xj(2),...,xj(n))T, x i , x j x_i,x_j xi,xj的 L p L_p Lp距离定义为
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p L_p(x_i,x_j)=(\sum\limits_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^p)^{\frac{1}{p}} Lp(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣p)p1
特别地,当 p = ∞ p=\infin p=∞时,它是各个坐标距离地最大值,即
L ∞ ( x i , x j ) = max l ∣ x i ( l ) − x j ( l ) ∣ L_{\infin}(x_i,x_j)=\max\limits_{l}|x_i^{(l)}-x_j^{(l)}| L∞(xi,xj)=lmax∣xi(l)−xj(l)∣
原理
k值的选择
k值较小容易发生过拟合
kd树
为了提高 k k k近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。具体方法有很多,下面介绍其中一种的 k d kd kd树(kd tree)方法。
k-d tree是每个节点均为k维数值点的二叉树,其上的每个节点代表一个超平面,该超平面垂直于当前划分维度的坐标轴,并在该维度上将空间划分为两部分,一部分在其左子树,另一部分在其右子树。即若当前节点的划分维度为d,其左子树上所有点在d维的坐标值均小于当前值,右子树上所有点在d维的坐标值均大于等于当前值。
kd树的构造
对深度为 j j j的结点,选择 x ( l ) x^{(l)} x(l)为切分的坐标轴, l = j ( m o d k ) + 1 l=j(mod\ k)+1 l=j(mod k)+1,然后划分为左子树和右子树递归构造
kd树的查找
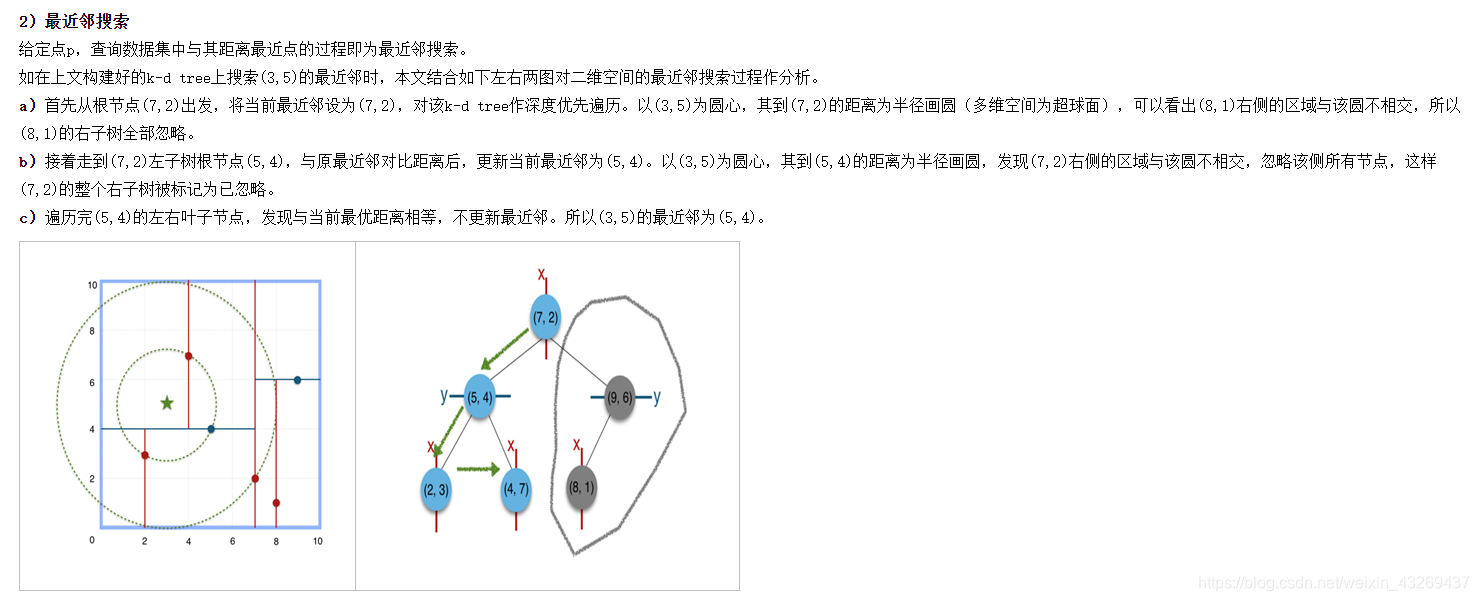
时间复杂度 O ( l o g ( N ) ) O(log(N)) O(log(N))
疑问
上图中第一次查找时,(8,1)确实更远,但是如果改成(7,4)还需要搜索右边的点吗。
答:不可能出现这种情况。上面描述有误吗,不能拿(8,1)参考,而是应该拿(9,6)参考,因为按照划分的顺序,(9,6)是父节点。也不可能出现疑问中的情况。
代码
不想写了。。累了。
贴一个掉包,kd-tree的代码有空再补。。主要是py不熟。
import numpy as np
from sklearn.neighbors import KDTree
np.random.seed(0)
points = np.random.random([15,2])
tree = KDTree(points)
point = points[0]
print(points)
print(point)
print("========================")
dists, indices = tree.query([point], k = 3)
p