算法训练|买卖股票的最佳时机 II (贪心、动态规划)

贪心

思路:题目没有说明交易次数、因此采用每天都交易的方式不断交易，用第二天的股票价格-前一天的股票价格，如果得到的值大于0，则添加进收益和。一直增加，直到收益达到最大。

class Solution {
    
    
    public int maxProfit(int[] prices) {
    
    
        int profit = 0;
        int length = prices.length;
        for (int i = 1; i < length; i++) {
    
    
        	//不断交易
            int sum = prices[i] - prices[i-1];
            if(sum>0){
    
    
            	//如果收益大于0，则添加收益和
                profit += sum;
            }
        }
        return profit;
    }
}

动态规划

动态规划的第一步
找出最后一步和子问题

这题中，最后一步是求解最后一天，即第i天的最大收益，子问题是，求解前一天的最大收益，即第i-1天的最大收益。

动态规划的第二步
求解问题的状态转移方程

定义状态dp[i][0]表示第i天交易完成后手里没有股票的最大收益，dp[i][1]表示第i天交易完成后手里有一支股票的最大收益。

对两个状态进行分析
dp[i][0]有两种情况，第一种是前一天手里就没有股票了，即dp[i-1][0]，第二种是前一天手里有一支股票，但是在第i天卖出了，此时获得了收益prices[i],即dp[i-1][1]+prices[i]得到的状态转移方程为:

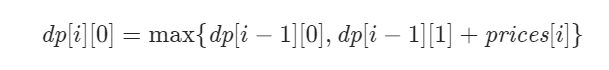
dp[i][1]也有两种情况,第一种情况是前一天持有一支股票，但是没有卖出，即dp[i-1][1]，第二种情况是前一天没有股票，但是在第i天买了一支股票，此时收益为负的，为-prices[i]，即dp[i-1][0]-prices[i]得到的状态转移方程为:

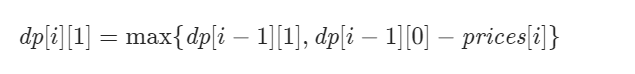
动态规划的第三步
求解边界情况

分析可知，dp[0][0] =0,表示最开始的初始状态，dp[0][1] = -prices[0],表示第一天交易之后的初始值。

因此可以写出代码

class Solution {
    
    
    public int maxProfit(int[] prices) {
    
    
        int price = 0;

        int length = prices.length;
        int dp[][] = new int[length][2];
        dp[0][0] = 0;
        dp[0][1] =-prices[0];
        for (int i = 1; i < length; i++) {
    
    
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
        }
        return dp[length-1][0];
    }
}

因为最后一天持有股票的收益一定比不持有股票的收益要低，因此用不持有股票的状态来表示最后的最大收益。