C语言_最大公约数常用算法

四种方法分别为：辗转相除法、穷举法，更相减损法、
Stein算法
一、辗转相除法
1、函数嵌套调用流程图：

2、函数递归调用的程序流程图：

3、两个数的乘积=这两个数的最小公倍数*最大公约数
4、调试截图：
函数嵌套调用截图

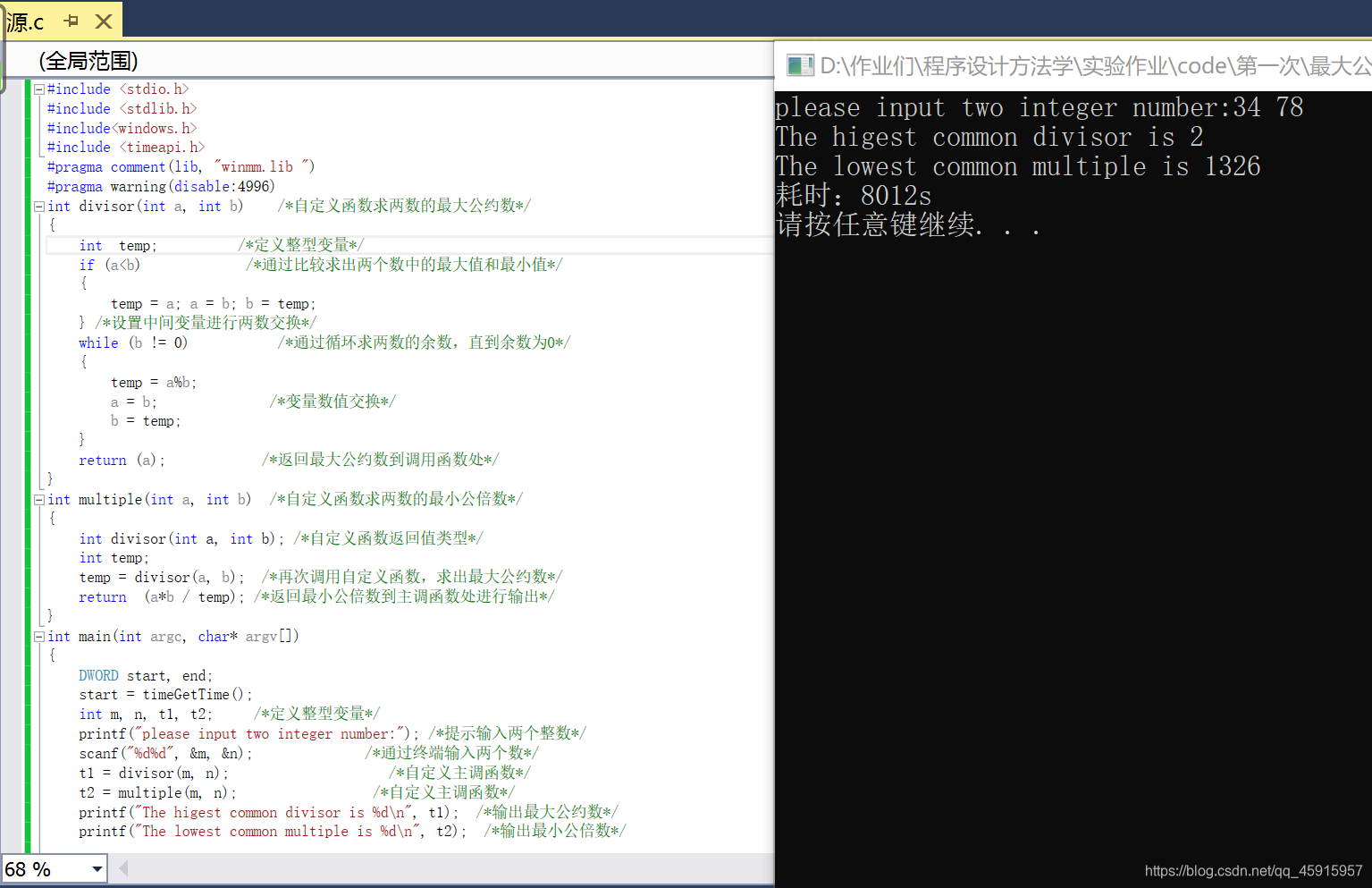
函数递归调用截图：

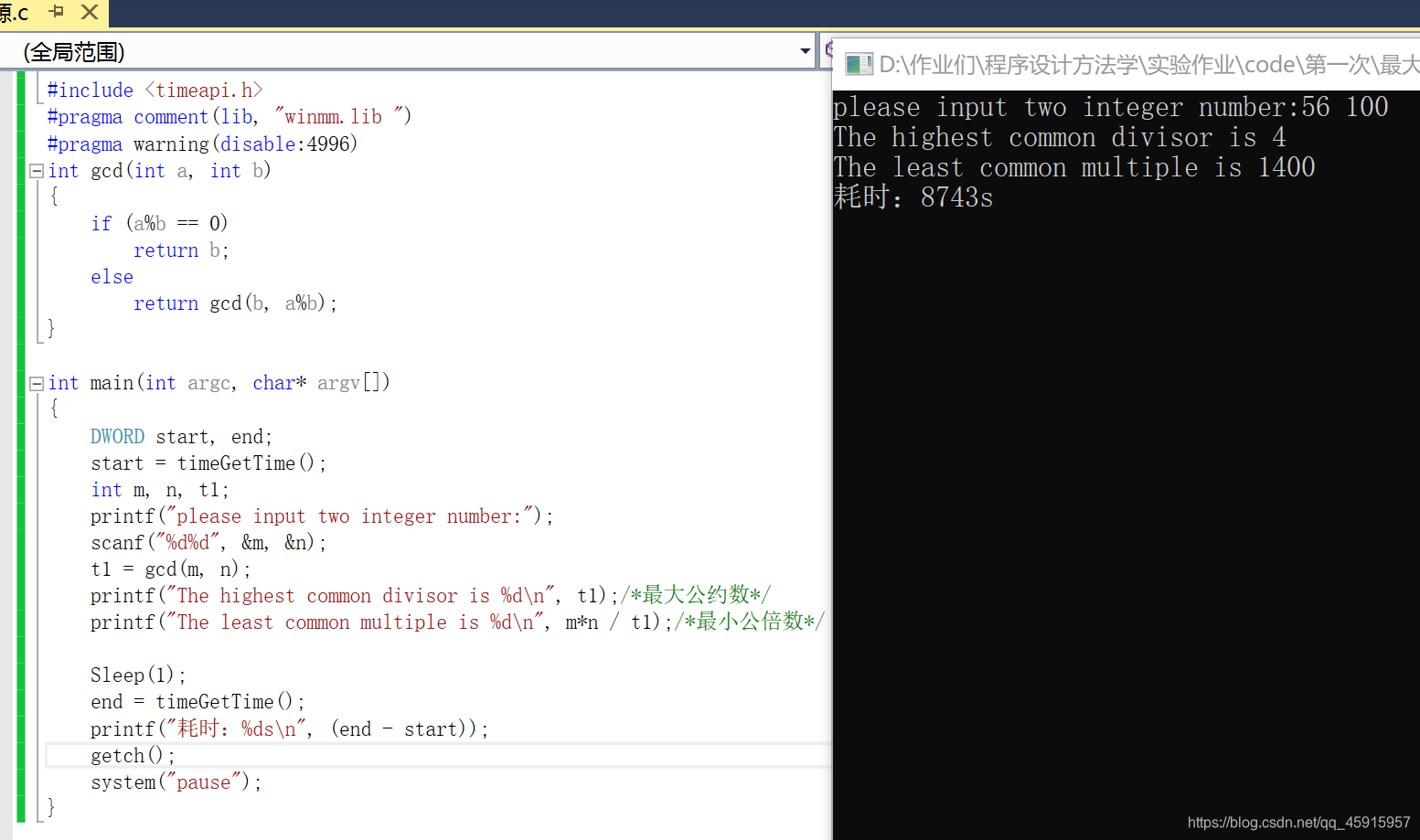
二、穷举法（利用数学定义）
穷举法（也叫枚举法）穷举法求两个正整数的最大公约数的解题步骤：从两个数中较小数开始由大到小列举，直到找到公约数立即中断列举，得到的公约数便是最大公约数 。

①定义1：对两个正整数a,b如果能在区间[a,0]或[b,0]内能找到一个整数temp能同时被a和b所整除，则temp即为最大公约数。

②定义2：对两个正整数a,b,如果若干个a之和或b之和能被b所整除或能被a所整除，则该和数即为所求的最小公倍数。

求最大公约数的调试截图：

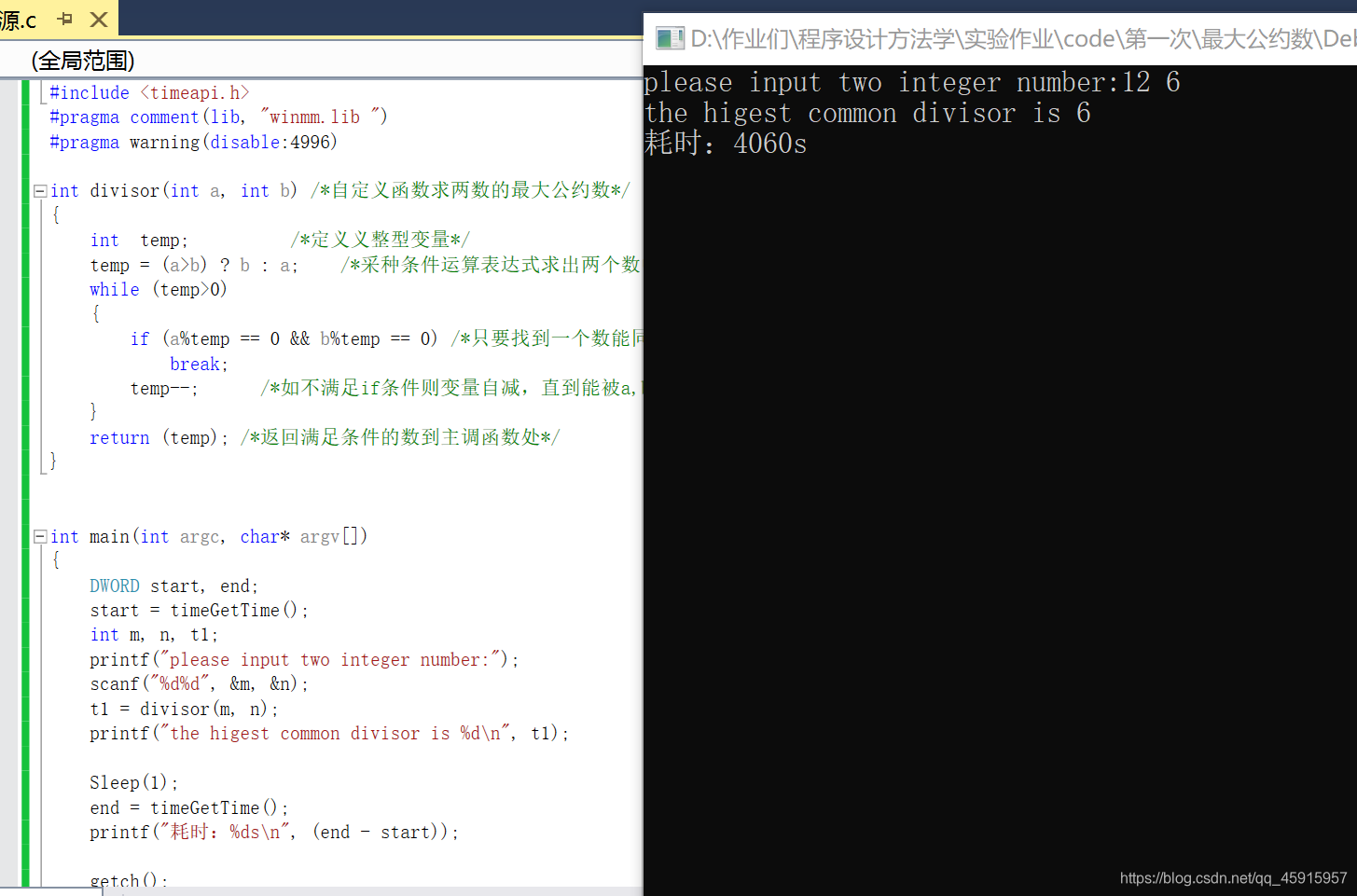
求最小公倍数的调试截图：

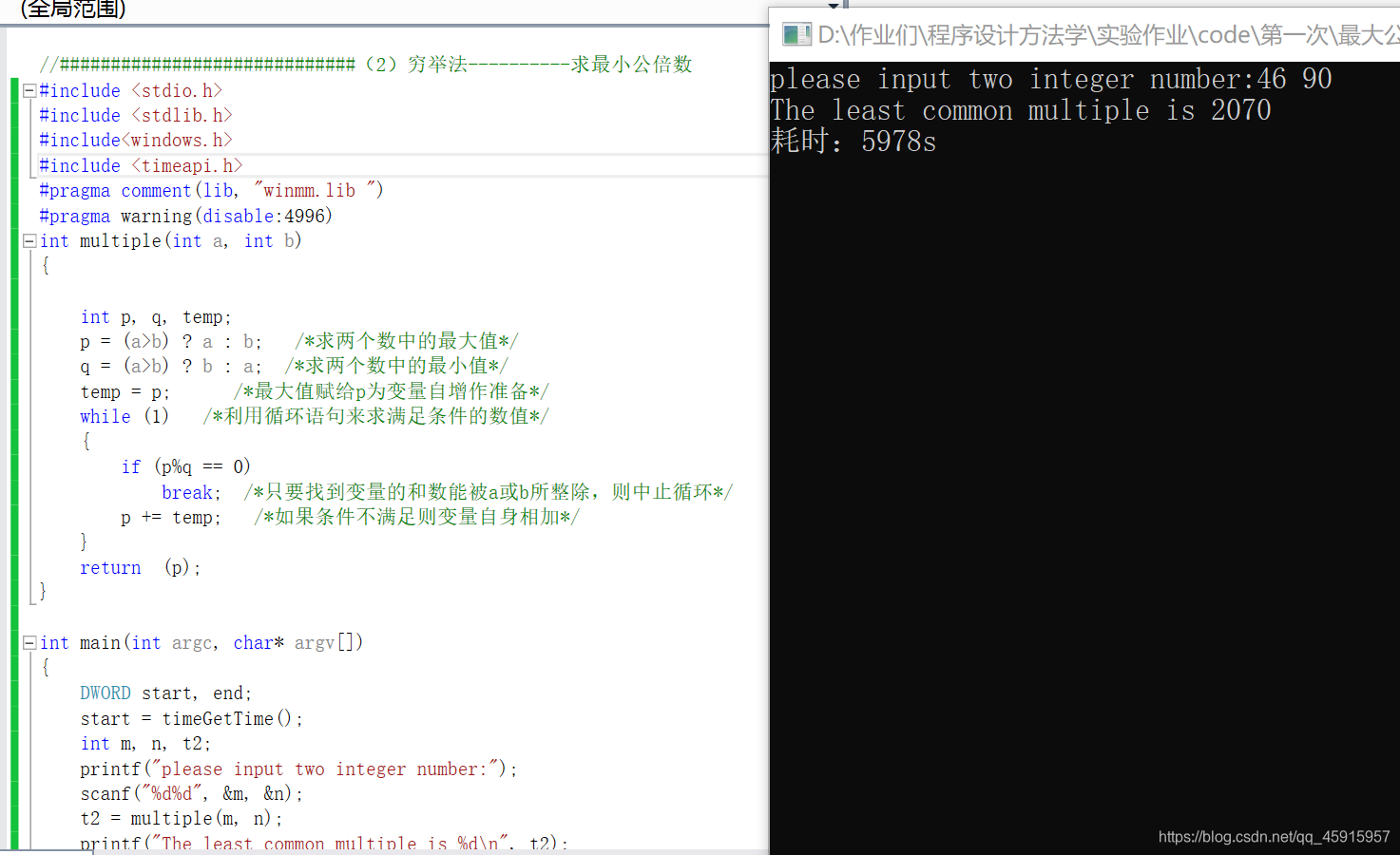
3. 更相减损法

(1)流程图

(2)调试截图

4.Stein算法

(1)流程图

(2)调试截图

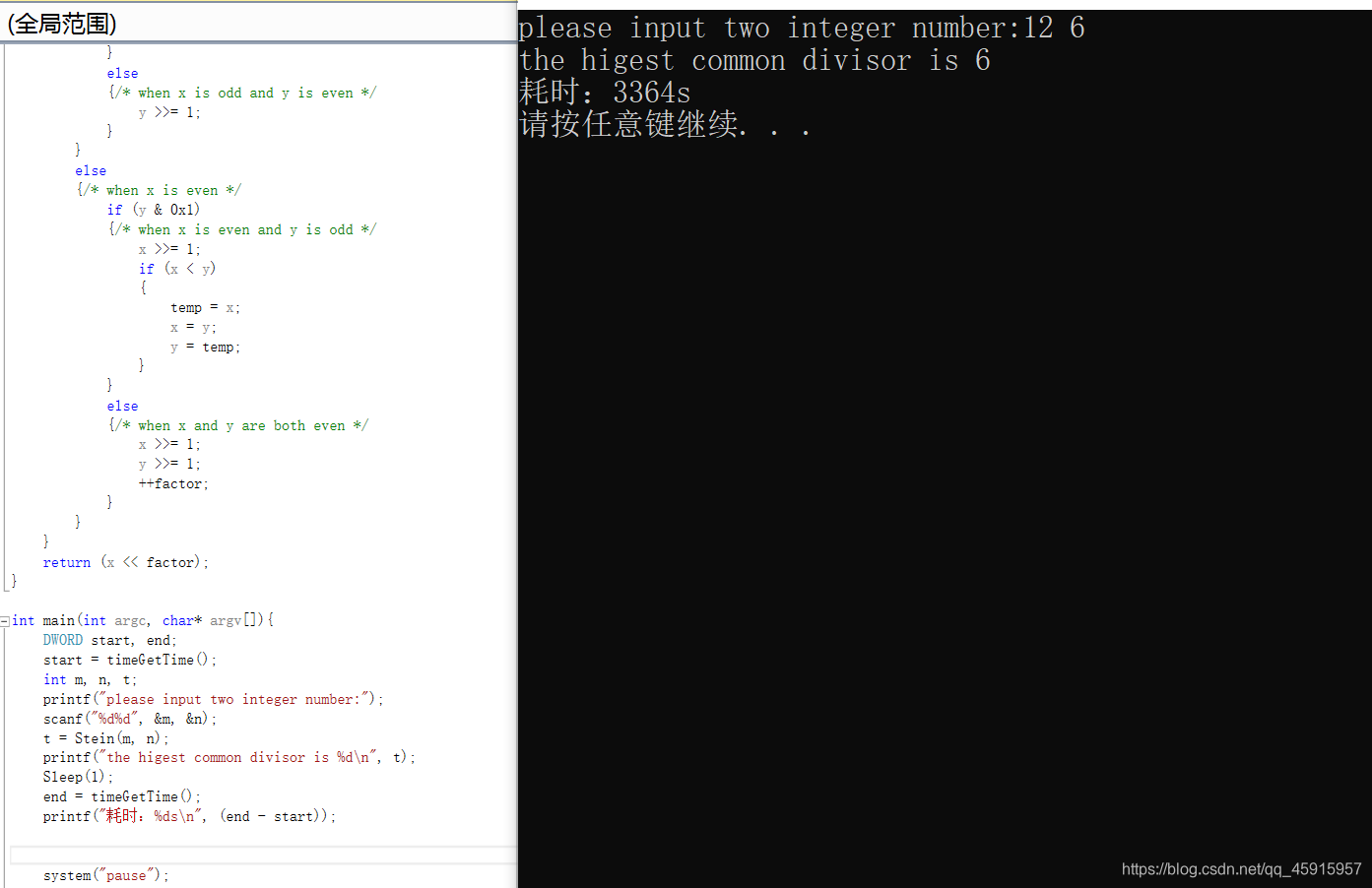
以上所用的计时函数为

#include <stdio.h>
#include <stdlib.h>
#include <windows.h>
#include <timeapi.h>

#pragma comment(lib, "winmm.lib ")

int main(int argc, char* argv[])
{
    
    
    DWORD start, end;
    start = timeGetTime();
    Sleep(1);
    end = timeGetTime();
    printf("耗时：%ds\n", (end - start));

    system("pause");
    return 0;
}