00 前言
在RoboMaster比赛中,由于工业相机帧率、算法效率、信息传输速率等影响,我们通常需要对目标进行预测,才能更好的击中装甲板。
首先感谢robomaster比赛中各个学校开源的代码和各类教程和代码,共同进步,以及感谢卡尔曼滤波作者Rudolf Emil Kalman。
原论文地址:http://www.cs.unc.edu/~welch/kalman/media/pdf/Kalman1960.pdf
如本文出现错误欢迎指出,一起学习交流共同进步
01 卡尔曼滤波简介
百度百科:卡尔曼滤波(Kalman filtering)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
数据滤波是去除噪声还原真实数据的一种数据处理技术,Kalman滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中,估计动态系统的状态。由于它便于计算机编程实现,并能够对现场采集的数据进行实时的更新和处理,Kalman滤波是目前应用最为广泛的滤波方法,在通信,导航,制导与控制等多领域得到了较好的应用。
卡尔曼滤波的应用领域非常广泛,在航空航天、信息技术等领域尤为广泛。
02 卡尔曼滤波概要
由于我们在实际工程中,测量往往存在很多不确定性,这些不确定性包括有1)不存在完美的数学模型;2)系统的扰动是不可控的,也很难建模的;3)测量的传感器本身存在着误差。而影响我们这种误差的称为噪声,例如我们在使用PNP测距的时候,远距离是非常不精确的,它的波动可能会很大,这个时候我们就需要进行一下滤波,如下图所示(蓝色为滤波后数据、红色为实际测量值、绿色为理想测量值)
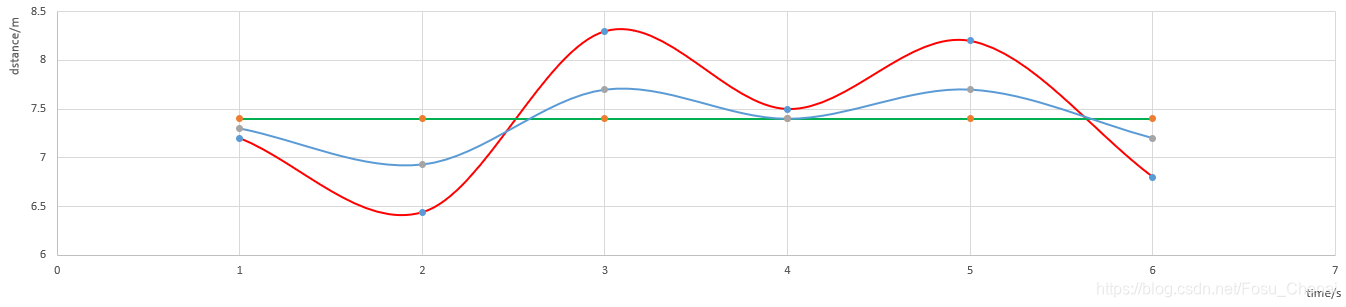
在我的理解里,卡尔曼滤波就相当于一个带有权重的低通滤波,即调整观测值的权重(测量值)和估计值的权重,是更相信观测值还是更相信估计值的一个过程,观测值*权重+估计值*权重 = 修正值,即最优估计。
Kalman滤波是一种递归过程,主要两个更新过程:时间更新和观测更新,其中时间更新主要包括状态预测和协方差预测,主要是对系统的预测,而观测更新主要包括计算卡尔曼增益、状态更新和协方差更新,因此整个递归过程主要包括五个方面的计算:
1、状态预测;
2、协方差预测;
3、卡尔曼增益
4、状态更新(修正);
5、协方差更新(修正);
卡尔曼滤波的适用条件主要有:
1、应用系统必须是线性的;
2、对测量造成影响的噪声必须是符合高斯分布的白噪声。
白噪声:是一种功率谱密度为常数的随机信号或随机过程。即此信号在各个频段上的功率一致。其余的统称为有色噪声
03 卡尔曼公式推导及理解
3.1 基本模型
在介绍卡尔曼公式理解前先介绍一下状态空间方程,便于后面的公式理解。
状态方程:
x k = A x k − 1 + B u k − 1 + ω k − 1 x_k = Ax_{k-1} + Bu_{k-1} + \omega_{k-1} xk=Axk−1+Buk−1+ωk−1
观测方程:
z k = H x k + υ k z_k = Hx_k + \upsilon_k zk=Hxk+υk
x k x_k xk:当前 k k k时刻的系统状态
x k − 1 x_{k-1} xk−1: k − 1 k-1 k−1时刻的系统状态
A A A:传输参数
B B B:控制参数
u k − 1 u_{k-1} uk−1: k − 1 k-1 k−1对系统的控制量
z k z_k zk: k k k时刻的测量值或观测值
H H H:状态转移矩阵
ω k − 1 \omega_{k-1} ωk−1和 υ k \upsilon_k υk:分别为 k − 1 k-1 k−1时刻的过程噪声和 k k k时刻的观测噪声。
过程噪声和观测噪声假设是符合高斯分布,即:
p ( ω k ) ∼ N ( 0 , Q ) p ( υ k ) ∼ N ( 0 , R ) p(\omega_k) \sim N(0, Q)\\ p(\upsilon_k) \sim N(0, R) p(ωk)∼N(0,Q)p(υk)∼N(0,R)
ω k \omega_k ωk:过程噪声
υ k \upsilon_k υk:观测噪声
Q Q Q:过程噪声协方差矩阵
R R R:观测噪声协方差矩阵
3.2卡尔曼公式
时间更新:
x ^ k − = A x ^ k − 1 + B u k − 1 P k − = A P k − 1 A T + Q \hat{x}^{-}_k = A\hat{x}_{k-1}+Bu_{k-1}\\ P^-_k = AP_{k-1}A^{T} + Q x^k−=Ax^k−1+Buk−1Pk−=APk−1AT+Q
状态更新:
K k = P k − H T ( H P k − H T + R ) − 1 x ^ k = x ^ k − + K k ( z k − H x ^ k − ) P k = ( I − K k H ) P k − K_k = P^-_kH^{T}(HP^-_kH^{T} + R)^{-1} \\ \hat{x}_k = \hat{x}^-_k + K_k(z_k - H\hat{x}^-_k)\\ P_k = (I - K_kH)P^-_k Kk=Pk−HT(HPk−HT+R)−1x^k=x^k−+Kk(zk−Hx^k−)Pk=(I−KkH)Pk−
x ^ k − \hat{x}^-_k x^k−:当前状态先验估计值
x ^ k − 1 \hat{x}_{k-1} x^k−1:上一状态的最优估计
u k − 1 u_{k-1} uk−1:上一状态的系统控制量
P k − P^-_k Pk−:当前状态先验估计值的协方差
P k − 1 P_{k-1} Pk−1:上一状态的协方差修正值
A A A:状态转移矩阵
B B B:控制矩阵
Q Q Q:过程噪声的方差
K k K_k Kk:当前状态的卡尔曼增益(Kalman Gain)
H H H:观测系统的参数
R R R:测量噪声的方差
I I I:单位矩阵
协方差( c o v ( X , Y ) cov(X, Y) cov(X,Y))可以理解为 X 、 Y X、Y X、Y两个变量的数值上的相关性,即正相关还是负相关
均方误差:误差的平方的期望值,也就是多个样本的时候,均分误差等于每个样本的误差的平方乘以该样本出现的概率和
方差:方差是描述随机变量的离散程度,是变量离期望值的距离
两个变量间的协方差:
c o v ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] = E ( X Y ) − E ( X ) E ( Y ) cov(X, Y) = E[(X-E(X))(Y-E(Y))] = E(XY) - E(X)E(Y) cov(X,Y)=E[(X−E(X))(Y−E(Y))]=E(XY)−E(X)E(Y)
它表示两个变量之间的总体误差,当 Y = X Y=X Y=X的时候,就是方差 D ( X ) = D ( Y ) D(X) = D(Y) D(X)=D(Y)。
我们将均值去掉
( X − E ( X ) ) ( Y − E ( Y ) ) (X-E(X))(Y-E(Y)) (X−E(X))(Y−E(Y))
就成了两个公式相乘,即当样本数据 X X X大于自身期望, Y Y Y也大于自身期望时,那么协方差就为正值,为正相关,反之为负相关。
在现实生活中,我们常常会遇到多维的数据,方差是不足以满足我们的需求的,所以我们要引入协方差来处理多维的数据。
通俗理解就是使用上一个状态的最优估计(后验估计)来得出当前的先验估计,在由当前的观测值来修正得到最优估计,即后验估计的一个递归过程。
3.3卡尔曼公式推导
时间更新公式:
x ^ k − = A x ^ k − 1 + B u k P k − = A P k − 1 A T + Q \hat{x}^{-}_k = A\hat{x}_{k-1}+Bu_{k}\\ P^-_k = AP_{k-1}A^{T} + Q x^k−=Ax^k−1+BukPk−=APk−1AT+Q
其中 x ^ k − = F x ^ k − 1 + B u k \hat{x}^{-}_k = F\hat{x}_{k-1}+Bu_{k} x^k−=Fx^k−1+Buk为状态空间方程去除过程噪声得到的先验估计推导公式
关于
P k − = A P k − 1 A T + Q P^-_k = AP_{k-1}A^{T} + Q Pk−=APk−1AT+Q
我们知道
c o v ( a X + B , a X + B ) = a c o v ( X , X ) a T cov(aX+B,aX+B)= acov(X,X)a^T cov(aX+B,aX+B)=acov(X,X)aT
那么
c o v ( x ^ k − , x ^ k − ) = c o v ( A x ^ k − 1 + B u k , A x ^ k − 1 + B u k ) = A c o v ( x ^ k − 1 , x ^ k − 1 ) A T + Q cov(\hat{x}^{-}_k,\hat{x}^{-}_k) = cov(A\hat{x}_{k-1}+Bu_{k},A\hat{x}_{k-1}+Bu_{k}) \\ = Acov(\hat{x}_{k-1},\hat{x}_{k-1})A^T + Q cov(x^k−,x^k−)=cov(Ax^k−1+Buk,Ax^k−1+Buk)=Acov(x^k−1,x^k−1)AT+Q
这个 Q Q Q是过程噪声的协方差,即 c o v ( ω k , ω k ) cov(\omega_k,\omega_k) cov(ωk,ωk)
故
P k − = c o v ( x ^ k − , x ^ k − ) = A c o v ( x ^ k − 1 , x ^ k − 1 ) A T + Q = A P k − 1 A T + Q P^-_k = cov(\hat{x}^{-}_k,\hat{x}^{-}_k) =Acov(\hat{x}_{k-1},\hat{x}_{k-1})A^T + Q = AP_{k-1}A^{T} + Q Pk−=cov(x^k−,x^k−)=Acov(x^k−1,x^k−1)AT+Q=APk−1AT+Q
状态更新公式:
K k = P k − H T ( H P k − H T + R ) − 1 x ^ k = x ^ k − + K k ( z k − H x ^ k − ) P k = ( I − K k H ) P k − K_k = P^-_kH^{T}(HP^-_kH^{T} + R)^{-1} \\ \hat{x}_k = \hat{x}^-_k + K_k(z_k - H\hat{x}^-_k)\\ P_k = (I - K_kH)P^-_k Kk=Pk−HT(HPk−HT+R)−1x^k=x^k−+Kk(zk−Hx^k−)Pk=(I−KkH)Pk−
关于 x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_k = \hat{x}^-_k + K_k(z_k - H\hat{x}^-_k) x^k=x^k−+Kk(zk−Hx^k−),我们可以通过一个一维的例子来对该公式进行一个引入,例如:
我们需要测量一个物体的长度,通常我们都会通过多次测量进而取平均值,即
x ^ k = 1 k ( z 1 + z 2 + z 3 + . . . + z k ) = 1 k ( z 1 + z 2 + z 3 + . . . + z k − 1 ) + 1 k z k = 1 k k − 1 k − 1 ( z 1 + z 2 + z 3 + . . . + z k − 1 ) + 1 k z k = k − 1 k x ^ k − 1 + 1 k z k = x ^ k − 1 − 1 k x ^ k − 1 + 1 k z k \begin{aligned} \hat{x}_k &= \frac{1}{k}(z_1+z_2+z_3+...+z_k)\\ &= \frac{1}{k}(z_1+z_2+z_3+...+z_{k-1}) + \frac{1}{k}z_k\\ &= \frac{1}{k} \frac{k-1}{k-1}(z_1+z_2+z_3+...+z_{k-1})+\frac{1}{k}z_k\\ &= \frac{k-1}{k}\hat{x}_{k-1}+\frac{1}{k}z_k\\ &= \hat{x}_{k-1}-\frac{1}{k}\hat{x}_{k-1}+\frac{1}{k}z_k \end{aligned} x^k=k1(z1+z2+z3+...+zk)=k1(z1+z2+z3+...+zk−1)+k1zk=k1k−1k−1(z1+z2+z3+...+zk−1)+k1zk=kk−1x^k−1+k1zk=x^k−1−k1x^k−1+k1zk
所以
x ^ k = x ^ k − 1 + 1 k ( z k − x ^ k − 1 ) \hat{x}_k = \hat{x}_{k-1}+\frac{1}{k}(z_k-\hat{x}_{k-1}) x^k=x^k−1+k1(zk−x^k−1)
我们将
1 k = K k \frac{1}{k} = K_k k1=Kk
则
x ^ k = x ^ k − 1 + K k ( z k − x ^ k − 1 ) \hat{x}_k = \hat{x}_{k-1}+K_k(z_k-\hat{x}_{k-1}) x^k=x^k−1+Kk(zk−x^k−1)
即当前的估计值 = 上一次的估计值+系数x(当前的测量值-上一次的估计值)
而在卡尔曼滤波中,我们将这个系数 K k K_k Kk称为卡尔曼增益(Kalman Gain)
而在多维的情况下已知状态空间方程:
x k = A x k − 1 + B u k − 1 + ω k − 1 z k = H x k + υ k x_k = Ax_{k-1} + Bu_{k-1} + \omega_{k-1}\\ z_k = Hx_k + \upsilon_k xk=Axk−1+Buk−1+ωk−1zk=Hxk+υk
而这个 ω k − 1 \omega_{k-1} ωk−1和 υ k \upsilon_k υk是我们没办法建模的,所以,我们只取前面部分作为估计值
即
x ^ k − = A x ^ k − 1 + B u k − 1 z k = H x k \hat{x}^-_k = A\hat{x}_{k-1} + Bu_{k-1}\\ z_k = Hx_k x^k−=Ax^k−1+Buk−1zk=Hxk
而
z k = H x k ⇒ x k = H − z k z_k = Hx_k \Rightarrow x_k = H^-z_k zk=Hxk⇒xk=H−zk
由刚刚的当前的值 x ^ k = \hat{x}_k= x^k=算出来的结果 x ^ − \hat{x}^- x^−+系数 G ∗ ( G*( G∗(测出来的结果 H − z k − H^-z_k- H−zk−算出来的结果 x k − ) x^-_k) xk−)
所以有
x ^ k = x ^ k − + G ( H − z k − x ^ k − ) \hat{x}_k = \hat{x}^-_k+G(H^-z_k- \hat{x}^-_k) x^k=x^k−+G(H−zk−x^k−)
即当 G = 0 G = 0 G=0的时候, x ^ k = x ^ k − \hat{x}_k = \hat{x}^-_k x^k=x^k−,即相信估计值,当 G = 1 G = 1 G=1的时候, x ^ k = H − z k \hat{x}_k = H^-z_k x^k=H−zk,即更相信测量值。
而在卡尔曼滤波中, G = K k H G = K_kH G=KkH,代入就可以得到:
x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_k = \hat{x}^-_k + K_k(z_k - H\hat{x}^-_k) x^k=x^k−+Kk(zk−Hx^k−)
所以当 K k = 0 K_k = 0 Kk=0时, x ^ k = x ^ k − \hat{x}_k=\hat{x}^-_k x^k=x^k−;当 K k = H − K_k = H^- Kk=H−时, x ^ k = H − z k \hat{x}_k = H^-z_k x^k=H−zk。
这里我们引入真实值与估计值的误差 e k e_k ek和真实值与先验估计的误差:
e k = x k − x ^ k e k − = x k − x ^ k − e_k = x_k - \hat{x}_k\\ e_k^-=x_k-\hat{x}^-_k ek=xk−x^kek−=xk−x^k−
我们假设这个误差也符合高斯分布,即 p ( e k ) ∼ N ( 0 , P ) p(e_k)\sim N(0,P) p(ek)∼N(0,P),这里的协方差矩阵 P = E [ e e T ] P = E[ee^T] P=E[eeT]
重点:如果我们新估计的结果 x ^ k \hat{x}_k x^k与实际值 x k x_k xk最小呢,也就是说它整个的误差的方差最小,方差越小,那么它的期望值越接近于0,所以我们需要选取一个合适的值,使得它的协方差矩阵 P P P的迹 t r ( P ) tr(P) tr(P)最小。
已知 e k = x k − x ^ k e_k = x_k - \hat{x}_k ek=xk−x^k,那么
P k = E [ e k e k T ] = E [ ( x k − x ^ k ) ( x k − x ^ k ) T ] P_k = E[e_ke^T_k] = E[(x_k - \hat{x}_k)(x_k - \hat{x}_k)^T] Pk=E[ekekT]=E[(xk−x^k)(xk−x^k)T]
因为我们要求 K k K_k Kk,那么我们将 x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_k = \hat{x}^-_k + K_k(z_k - H\hat{x}^-_k) x^k=x^k−+Kk(zk−Hx^k−)代入上式中
先化简一下 x k − x ^ k x_k-\hat{x}_k xk−x^k:
x k − x ^ k = x k − ( x ^ k − + K k ( z k − H x ^ k − ) ) = x k − x ^ k − − K k z k + K k H x ^ k − = x k − x ^ k − − K k H x k − K k v k + K k H x ^ k − = ( x k − x ^ k − ) − K k H ( x k − x ^ k − ) − K k v k = ( I − K k H ) ( x k − x ^ k − ) − K k v k = ( I − K k H ) e k − − K k v k \begin{aligned} x_k-\hat{x}_k &= x_k-(\hat{x}^-_k + K_k(z_k - H\hat{x}^-_k))\\ &=x_k-\hat{x}^-_k-K_kz_k+K_kH\hat{x}^-_k\\ &=x_k-\hat{x}^-_k-K_kHx_k-K_kv_k+K_kH\hat{x}^-_k\\ &=(x_k-\hat{x}^-_k)-K_kH(x_k-\hat{x}^-_k)-K_kv_k\\ &=(I-K_kH)(x_k-\hat{x}^-_k)-K_kv_k\\ &=(I-K_kH)e^-_k-K_kv_k \end{aligned} xk−x^k=xk−(x^k−+Kk(zk−Hx^k−))=xk−x^k−−Kkzk+KkHx^k−=xk−x^k−−KkHxk−Kkvk+KkHx^k−=(xk−x^k−)−KkH(xk−x^k−)−Kkvk=(I−KkH)(xk−x^k−)−Kkvk=(I−KkH)ek−−Kkvk
那么
P k = E [ ( x k − x ^ k ) ( x k − x ^ k ) T ] = E [ [ ( I − K k H ) e k − − K k v k ] [ ( I − K k H ) e k − − K k v k ] T ] = E [ [ ( I − K k H ) e k − − K k v k ] [ e k − T ( I − K k H ) T − v k T K k T ] ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T − ( I − K k H ) e k − v k T K k T − K k v k [ e k − T ( I − K k H ) T + K k v k v k T K k T ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T ] − E [ ( I − K k H ) e k − v k T K k T ] − E [ K k v k [ e k − T ( I − K k H ) T ] + E [ K k v k v k T K k T ] \begin{aligned} P_k &= E[(x_k - \hat{x}_k)(x_k - \hat{x}_k)^T]\\ &=E[[(I-K_kH)e^-_k-K_kv_k][(I-K_kH)e^-_k-K_kv_k]^T]\\ &=E[[(I-K_kH)e^-_k-K_kv_k][e^{-T}_k(I-K_kH)^T-v_k^TK_k^T]]\\ &=E[(I-K_kH)e^-_ke^{-T}_k(I-K_kH)^T-(I-K_kH)e^-_kv_k^TK_k^T-K_kv_k[e^{-T}_k(I-K_kH)^T+K_kv_kv_k^TK_k^T]\\ &=E[(I-K_kH)e^-_ke^{-T}_k(I-K_kH)^T]-E[(I-K_kH)e^-_kv_k^TK_k^T]-E[K_kv_k[e^{-T}_k(I-K_kH)^T]+E[K_kv_kv_k^TK_k^T] \end{aligned} Pk=E[(xk−x^k)(xk−x^k)T]=E[[(I−KkH)ek−−Kkvk][(I−KkH)ek−−Kkvk]T]=E[[(I−KkH)ek−−Kkvk][ek−T(I−KkH)T−vkTKkT]]=E[(I−KkH)ek−ek−T(I−KkH)T−(I−KkH)ek−vkTKkT−Kkvk[ek−T(I−KkH)T+KkvkvkTKkT]=E[(I−KkH)ek−ek−T(I−KkH)T]−E[(I−KkH)ek−vkTKkT]−E[Kkvk[ek−T(I−KkH)T]+E[KkvkvkTKkT]
第二项
E [ ( I − K k H ) e k − v k T K k T ] = ( I − K k H ) E ( e k − v k T ) K k T E[(I-K_kH)e^-_kv_k^TK_k^T] = (I-K_kH)E(e^-_kv^T_k)K^T_k E[(I−KkH)ek−vkTKkT]=(I−KkH)E(ek−vkT)KkT
因为 e k − e^-_k ek−与 v k T v^T_k vkT是相互独立的,即先验误差和测量误差是没有什么关系的,所以
E ( e k − v k T ) = E ( e k − ) E ( v k T ) E(e^-_kv^T_k) = E(e^-_k)E(v^T_k) E(ek−vkT)=E(ek−)E(vkT)
又因为 p ( v k T ) ∼ N ( 0 , R k ) p(v^T_k)\sim N(0, R_k) p(vkT)∼N(0,Rk)以及 p ( e k − ) ∼ N ( 0 , P ) p(e^-_k)\sim N(0,P) p(ek−)∼N(0,P),所以
E ( e k − ) = E ( v k T ) = 0 E(e^-_k) = E(v^T_k) = 0 E(ek−)=E(vkT)=0
所以
E [ ( I − K k H ) e k − v k T K k T ] = 0 E[(I-K_kH)e^-_kv_k^TK_k^T] = 0 E[(I−KkH)ek−vkTKkT]=0
同理第三项
E [ K k v k [ e k − T ( I − K k H ) T ] ] = K k E ( v k ) E ( e k − T ) ( I − K k H ) T = 0 E[K_kv_k[e^{-T}_k(I-K_kH)^T]] = K_kE(v_k)E(e^{-T}_k)(I-K_kH)^T = 0 E[Kkvk[ek−T(I−KkH)T]]=KkE(vk)E(ek−T)(I−KkH)T=0
故
P k = E [ ( x k − x ^ k ) ( x k − x ^ k ) T ] = E [ [ ( I − K k H ) e k − − K k v k ] [ ( I − K k H ) e k − − K k v k ] T ] = E [ [ ( I − K k H ) e k − − K k v k ] [ e k − T ( I − K k H ) T − v k T K k T ] ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T − ( I − K k H ) e k − v k T K k T − K k v k [ e k − T ( I − K k H ) T + K k v k v k T K k T ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T ] − E [ ( I − K k H ) e k − v k T K k T ] − E [ K k v k [ e k − T ( I − K k H ) T ] + E [ K k v k v k T K k T ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T ] + E [ K k v k v k T K k T ] = ( I − K k H ) E ( e k − e k − T ) ( I − K k H ) T + K k E ( v k v k T ) K k T \begin{aligned} P_k &= E[(x_k - \hat{x}_k)(x_k - \hat{x}_k)^T]\\ &=E[[(I-K_kH)e^-_k-K_kv_k][(I-K_kH)e^-_k-K_kv_k]^T]\\ &=E[[(I-K_kH)e^-_k-K_kv_k][e^{-T}_k(I-K_kH)^T-v_k^TK_k^T]]\\ &=E[(I-K_kH)e^-_ke^{-T}_k(I-K_kH)^T-(I-K_kH)e^-_kv_k^TK_k^T-K_kv_k[e^{-T}_k(I-K_kH)^T+K_kv_kv_k^TK_k^T]\\ &=E[(I-K_kH)e^-_ke^{-T}_k(I-K_kH)^T]-E[(I-K_kH)e^-_kv_k^TK_k^T]-E[K_kv_k[e^{-T}_k(I-K_kH)^T]+E[K_kv_kv_k^TK_k^T]\\ &=E[(I-K_kH)e^-_ke^{-T}_k(I-K_kH)^T]+E[K_kv_kv_k^TK_k^T]\\ &=(I-K_kH)E(e^-_ke^{-T}_k)(I-K_kH)^T+K_kE(v_kv^T_k)K^T_k \end{aligned} Pk=E[(xk−x^k)(xk−x^k)T]=E[[(I−KkH)ek−−Kkvk][(I−KkH)ek−−Kkvk]T]=E[[(I−KkH)ek−−Kkvk][ek−T(I−KkH)T−vkTKkT]]=E[(I−KkH)ek−ek−T(I−KkH)T−(I−KkH)ek−vkTKkT−Kkvk[ek−T(I−KkH)T+KkvkvkTKkT]=E[(I−KkH)ek−ek−T(I−KkH)T]−E[(I−KkH)ek−vkTKkT]−E[Kkvk[ek−T(I−KkH)T]+E[KkvkvkTKkT]=E[(I−KkH)ek−ek−T(I−KkH)T]+E[KkvkvkTKkT]=(I−KkH)E(ek−ek−T)(I−KkH)T+KkE(vkvkT)KkT
由于 P k = E ( e k e k T ) P_k=E(e_ke^T_k) Pk=E(ekekT),则
E ( e k − e k − T ) = P k − E(e^-_ke^{-T}_k) = P^-_k E(ek−ek−T)=Pk−
所以代入得
P k = ( I − K k H ) P k − ( I − K k H ) T + K k E ( v k v k T ) K k T = ( I P k − − K k H P k − ) ( I T − H T K k T ) + K k E ( v k v k T ) K k T \begin{aligned} P_k &= (I-K_kH)P^-_k(I-K_kH)^T+K_kE(v_kv^T_k)K^T_k\\ &=(IP^-_k-K_kHP^-_k)(I^T-H^TK^T_k)+K_kE(v_kv^T_k)K^T_k \end{aligned} Pk=(I−KkH)Pk−(I−KkH)T+KkE(vkvkT)KkT=(IPk−−KkHPk−)(IT−HTKkT)+KkE(vkvkT)KkT
又因为 p ( v k ) ∼ N ( 0 , R k ) p(v_k)\sim N(0, R_k) p(vk)∼N(0,Rk),即 E ( v k v k T ) = R k E(v_kv^T_k) = R_k E(vkvkT)=Rk,所以
P k = ( I − K k H ) P k − ( I − K k H ) T + K k E ( v k v k T ) K k T = ( P k − − K k H P k − ) ( I T − H T K k T ) + K k E ( v k v k T ) K k T = ( P k − − K k H P k − ) ( I T − H T K k T ) + K k R K k T = P k − − K k H P k − − P k − H T K k T + K k H P k − H T K k T + K k R K k T \begin{aligned} P_k &= (I-K_kH)P^-_k(I-K_kH)^T+K_kE(v_kv^T_k)K^T_k\\ &=(P^-_k-K_kHP^-_k)(I^T-H^TK^T_k)+K_kE(v_kv^T_k)K^T_k\\ &=(P^-_k-K_kHP^-_k)(I^T-H^TK^T_k)+K_kRK^T_k\\ &=P^-_k-K_kHP^-_k-P^-_kH^TK^T_k+K_kHP^-_kH^TK^T_k+K_kRK^T_k \end{aligned} Pk=(I−KkH)Pk−(I−KkH)T+KkE(vkvkT)KkT=(Pk−−KkHPk−)(IT−HTKkT)+KkE(vkvkT)KkT=(Pk−−KkHPk−)(IT−HTKkT)+KkRKkT=Pk−−KkHPk−−Pk−HTKkT+KkHPk−HTKkT+KkRKkT
我们要求的是 t r ( P k ) tr(P_k) tr(Pk),因为第三项的转置
( P k − H T K k T ) T = K k ( P k − H T ) T = K k H P k − T (P^-_kH^TK^T_k)^T = K_k(P^-_kH^T)^T = K_kHP^{-T}_k (Pk−HTKkT)T=Kk(Pk−HT)T=KkHPk−T
又因为协方差矩阵是对称矩阵,所以 P k − T = P k − P^{-T}_k=P^-_k Pk−T=Pk−,所以第二项和第三项互为转置,又因为互为转置,那么对角线上的元素是一样的,故 t r ( K k H P k − ) = t r ( P k − H T K k T ) tr(K_kHP^-_k)=tr(P^-_kH^TK^T_k) tr(KkHPk−)=tr(Pk−HTKkT),所以
t r ( P k ) = t r ( P k − ) − 2 t r ( K k H P k − ) + t r ( K k H P k − H T K k T ) + t r ( K k R K k T ) tr(P_k) = tr(P^-_k)-2tr(K_kHP^-_k)+tr(K_kHP^-_kH^TK^T_k)+tr(K_kRK^T_k) tr(Pk)=tr(Pk−)−2tr(KkHPk−)+tr(KkHPk−HTKkT)+tr(KkRKkT)
由于目标是寻找 K k K_k Kk使得 t r ( P k ) tr(P_k) tr(Pk)有最小值,所以我们令 t r ( P k ) tr(P_k) tr(Pk)对 K k K_k Kk求导,令其等于0,即
令 d t r ( P k ) d K k = 0 令\frac{dtr(P_k)}{dK_k} = 0 令dKkdtr(Pk)=0
所以
d t r ( P k ) d K k = 0 − d 2 t r ( K k H P k − ) d K k + d t r ( K k H P k − H T K k T ) d K k + d t r ( K k R K k T ) d K k \frac{dtr(P_k)}{dK_k} = 0-\frac{d2tr(K_kHP^-_k)}{dK_k}+\frac{dtr(K_kHP^-_kH^TK^T_k)}{dK_k}+\frac{dtr(K_kRK^T_k)}{dK_k} dKkdtr(Pk)=0−dKkd2tr(KkHPk−)+dKkdtr(KkHPk−HTKkT)+dKkdtr(KkRKkT)
这里需要一个用到两个矩阵微分公式
公式一:
d t r ( A B ) d A = B T \frac{dtr(AB)}{dA} = B^T dAdtr(AB)=BT
公式二:
d t r ( A B A T ) d A = 2 A B \frac{dtr(ABA^T)}{dA} = 2AB dAdtr(ABAT)=2AB
所以
d t r ( P k ) d K k = 0 − 2 ( H P k − ) T + 2 K k H P k − H T + 2 K k R \frac{dtr(P_k)}{dK_k} =0-2(HP^-_k)^T+2K_kHP^-_kH^T+2K_kR dKkdtr(Pk)=0−2(HPk−)T+2KkHPk−HT+2KkR
令其为0
d t r ( P k ) d K k = − 2 ( H P k − ) T + 2 K k H P k − H T + 2 K k R = 0 ⇒ − ( H P k − ) T + K k H P k − H T + K k R = 0 ⇒ − P k − H T + K k ( H P k − H T + R ) = 0 ⇒ K k ( H P k − H T + R ) = P k − H T \frac{dtr(P_k)}{dK_k} =-2(HP^-_k)^T+2K_kHP^-_kH^T+2K_kR=0\\ \Rightarrow-(HP^-_k)^T+ K_kHP^-_kH^T+ K_kR=0\\ \Rightarrow -P^-_kH^T+K_k(HP^-_kH^T+R)=0\\ \Rightarrow K_k(HP^-_kH^T+R) = P^-_kH^T dKkdtr(Pk)=−2(HPk−)T+2KkHPk−HT+2KkR=0⇒−(HPk−)T+KkHPk−HT+KkR=0⇒−Pk−HT+Kk(HPk−HT+R)=0⇒Kk(HPk−HT+R)=Pk−HT
所以
K k = P k − H T H P k − H T + R K_k = \frac{P^-_kH^T}{HP^-_kH^T+R} Kk=HPk−HT+RPk−HT
由上面可知
R = E ( v k v k T ) R = E(v_kv^T_k) R=E(vkvkT)
所以当 R R R特别大的时候,即测量噪声特别大时, K k → 0 K_k\rightarrow 0 Kk→0,这时 x ^ k = x ^ k − \hat{x}_k = \hat{x}^-_k x^k=x^k−;
当 R R R特别小的时候,即 R → 0 R\rightarrow0 R→0,这时 K k → H − K_k\rightarrow H^- Kk→H−,这时 x ^ k = H − z k \hat{x}_k = H^-z_k x^k=H−zk。
由上面的时间更新的推导,已知
P k − = c o v ( x ^ k − , x ^ k − ) = A c o v ( x ^ k − 1 , x ^ k − 1 ) A T + Q = A P k − 1 A T + Q P^-_k = cov(\hat{x}^{-}_k,\hat{x}^{-}_k) =Acov(\hat{x}_{k-1},\hat{x}_{k-1})A^T + Q = AP_{k-1}A^{T} + Q Pk−=cov(x^k−,x^k−)=Acov(x^k−1,x^k−1)AT+Q=APk−1AT+Q
即
P k − = A P k − 1 A T + Q P^-_k = AP_{k-1}A^{T} + Q Pk−=APk−1AT+Q
下面再推导一下 P k P_k Pk的修正公式
由刚刚推导 K k K_k Kk时的结论可知
P k = P k − − K k H P k − − P k − H T K k T + K k H P k − H T K k T + K k R K k T = P k − − K k H P k − − P k − H T K k T + K k ( H P k − K k T + R ) K k T \begin{aligned} P_k &= P^-_k-K_kHP^-_k-P^-_kH^TK^T_k+K_kHP^-_kH^TK^T_k+K_kRK^T_k\\ &=P^-_k-K_kHP^-_k-P^-_kH^TK^T_k+K_k(HP^-_kK^T_k + R)K^T_k \end{aligned} Pk=Pk−−KkHPk−−Pk−HTKkT+KkHPk−HTKkT+KkRKkT=Pk−−KkHPk−−Pk−HTKkT+Kk(HPk−KkT+R)KkT
我们将
K k = P k − H T H P k − H T + R K_k = \frac{P^-_kH^T}{HP^-_kH^T+R} Kk=HPk−HT+RPk−HT
代入上式
P k = P k − − K k H P k − − P k − H T K k T + P k − H T H P k − H T + R ( H P k − K k T + R ) K k T = P k − − K k H P k − − P k − H T K k T + P k − H T K k T = P k − − K k H P k − = ( I − K k H ) P k − \begin{aligned} P_k &= P^-_k-K_kHP^-_k-P^-_kH^TK^T_k+\frac{P^-_kH^T}{HP^-_kH^T+R}(HP^-_kK^T_k + R)K^T_k\\ &=P^-_k-K_kHP^-_k-P^-_kH^TK^T_k+P^-_kH^TK^T_k\\ &=P^-_k-K_kHP^-_k\\ &=(I-K_kH)P^-_k \end{aligned} Pk=Pk−−KkHPk−−Pk−HTKkT+HPk−HT+RPk−HT(HPk−KkT+R)KkT=Pk−−KkHPk−−Pk−HTKkT+Pk−HTKkT=Pk−−KkHPk−=(I−KkH)Pk−
故
P k = ( I − K k H ) P k − P_k = (I-K_kH)P^-_k Pk=(I−KkH)Pk−
到现在我们卡尔曼滤波的五个公式就全部推到完成了
| 时间更新 | 状态更新 |
|---|---|
| x ^ k − = A x ^ k − 1 + B u k − 1 \hat{x}^-_k=A\hat{x}_{k-1}+Bu_{k-1} x^k−=Ax^k−1+Buk−1 | K k = P k − H T ( H P k − H T + R ) − 1 K_k = P^-_kH^{T}(HP^-_kH^{T} + R)^{-1} Kk=Pk−HT(HPk−HT+R)−1 |
| P k − = A P k − 1 A T + Q P^-_k=AP_{k-1}A^T+Q Pk−=APk−1AT+Q | x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_k = \hat{x}^-_k + K_k(z_k - H\hat{x}^-_k) x^k=x^k−+Kk(zk−Hx^k−) |
| P k = ( I − K k H ) P k − P_k = (I - K_kH)P^-_k Pk=(I−KkH)Pk− |
04卡尔曼滤波超参数调节
已知
P k − = A P k − 1 A T + Q K k = P k − H T ( H P k − H T + R ) − 1 P^-_k=AP_{k-1}A^T+Q\\ K_k = P^-_kH^{T}(HP^-_kH^{T} + R)^{-1} Pk−=APk−1AT+QKk=Pk−HT(HPk−HT+R)−1
将 P k − P^-_k Pk−代入 K k K_k Kk中
K k = ( A P k − 1 A T + Q ) H T H ( A P k − 1 A T + Q ) H T + R = A P k − 1 A T H T + Q H T H A P k − 1 A T H T + Q H T + R \begin{aligned} K_k &= \frac{(AP_{k-1}A^T+Q)H^T}{H(AP_{k-1}A^T+Q)H^T+R}\\ &=\frac{AP_{k-1}A^TH^T+QH^T}{HAP_{k-1}A^TH^T+QH^T+R} \end{aligned} Kk=H(APk−1AT+Q)HT+R(APk−1AT+Q)HT=HAPk−1ATHT+QHT+RAPk−1ATHT+QHT
所以我们知道, K a l m a n Kalman Kalman G a i n Gain Gain的调节和过程噪声 Q Q Q以及观测噪声 R R R都有关系
再集合最优估计(后验估计)公式:
x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_k=\hat{x}^-_k+K_k(z_k-H\hat{x}^-_k) x^k=x^k−+Kk(zk−Hx^k−)
1)当我们要更信任观测值 z k z_k zk时,那么我们需要将 K k K_k Kk增大,所以可以将观测噪声 R R R调小
2)当我们要更信任估计值 x ^ k \hat{x}_k x^k时,那么我们需要将 K k K_k Kk调小,所以可以将 R R R调大,也可以将 Q Q Q调大
关于 x ^ 0 \hat{x}_0 x^0的取值和 P 0 P_0 P0的取值,我们习惯将 x ^ 0 = 0 , P 0 = 1 \hat{x}_0=0,P_0=1 x^0=0,P0=1
05 实际应用举例-RoboMaster预测跟踪
5.1 建立卡尔曼滤波器模型
我们将我们能获取到的状态向量定义为 x = [ θ p i t c h θ y a w ω p i t c h ω y a w ] x=\begin{bmatrix} \theta_{pitch} \\ \theta_{yaw} \\ \omega_{pitch} \\ \omega_{yaw} \end{bmatrix} x=⎣⎢⎢⎡θpitchθyawωpitchωyaw⎦⎥⎥⎤,控制向量 u = [ a p i t c h a y a w ] u=\begin{bmatrix} a_{pitch} \\ a_{yaw} \end{bmatrix} u=[apitchayaw],观测向量定义为 z = [ θ p i t c h θ y a w ω p i t c h ω y a w ] z=\begin{bmatrix} \theta_{pitch} \\ \theta_{yaw} \\ \omega_{pitch} \\ \omega_{yaw} \end{bmatrix} z=⎣⎢⎢⎡θpitchθyawωpitchωyaw⎦⎥⎥⎤。
1)状态预测:
根据变速运动模型运动方程: θ k = θ k − 1 + ω Δ t + a Δ t 2 \theta_k=\theta_{k-1}+\omega \Delta t+a\Delta t^2 θk=θk−1+ωΔt+aΔt2,得时间更新方程,角度的先验估计值:
x ^ k − = A x ^ k − 1 + B u k − 1 = [ 1 0 Δ t 0 0 1 0 Δ t 0 0 1 0 0 0 0 1 ] x ^ k − 1 + [ 1 2 Δ t 2 0 0 1 2 Δ t 2 Δ t 0 0 Δ t ] u k − 1 \begin{aligned} \hat{x}^-_k &= A\hat{x}_{k-1}+Bu_{k-1}\\ &=\begin{bmatrix} 1 & 0 & \Delta t & 0 \\ 0 & 1 & 0 & \Delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\hat{x}_{k-1}+\begin{bmatrix} \frac{1}{2\Delta t^2} & 0 \\ 0 & \frac{1}{2\Delta t^2} \\ \Delta t & 0 \\ 0 & \Delta t \end{bmatrix}u_{k-1} \end{aligned} x^k−=Ax^k−1+Buk−1=⎣⎢⎢⎡10000100Δt0100Δt01⎦⎥⎥⎤x^k−1+⎣⎢⎢⎡2Δt210Δt002Δt210Δt⎦⎥⎥⎤uk−1
A A A为状态转移矩阵(state transition matrix), B B B为控制矩阵(control matrix)
2)状态协方差矩阵(state covariance matrix)预测:
P k − = A P k − 1 A T + Q P^-_k = AP_{k-1}A^T+Q Pk−=APk−1AT+Q
Q Q Q为过程噪声(process covariance matrix)的协方差矩阵,即 c o v ( ω k , ω k ) = E ( ω k ω k T ) cov(\omega_k, \omega_k)=E(\omega_k\omega^T_k) cov(ωk,ωk)=E(ωkωkT)
3)更新卡尔曼增益
K k = A P k − 1 A T H T + Q H T H A P k − 1 A T H T + Q H T + R K_k = \frac{AP_{k-1}A^TH^T+QH^T}{HAP_{k-1}A^TH^T+QH^T+R} Kk=HAPk−1ATHT+QHT+RAPk−1ATHT+QHT
这是卡尔曼滤波器中最重要的一个值----卡尔曼增益(Kalman Gain)。 R R R为测量噪声的协方差矩阵(measurement covariance matrix),表示测量值与真实值之间的差距。
4)状态更新:
x ^ k = x ^ k − + K k ( z k − H x ^ k − ) \hat{x}_k = \hat{x}^-_k + K_k(z_k - H\hat{x}^-_k) x^k=x^k−+Kk(zk−Hx^k−)
完成了当前状态向量 x x x的更新,不仅考虑了上一时刻的预测值,也考虑了测量值,和整个系统的噪声。
5)协方差更新:
P k = ( I − K k H ) P k − P_k = (I - K_kH)P^-_k Pk=(I−KkH)Pk−
根据卡尔曼增益,更新系统的协方差 P k P_k Pk用于下一个周期中协方差( P k + 1 − P^-_{k+1} Pk+1−)预测的求解。
5.2 核心思想
核心思想:通过陀螺仪当前角度与装甲板相对云台角度的融合,得到装甲板在陀螺仪零轴上基坐标系上的绝对角度,将该角度输入至卡尔曼滤波器作为初始状态向量的角度值,之后主要作为观测向量的角度值。利用时间信息,经过新旧观测值相减,可以得到速度和加速度,输入到目标模型,目标运动模型选用变加速度模型,经过卡尔曼滤波器的更新预测,输出预测角度,实现对装甲板目标的预测跟踪。
5.3 算法流程
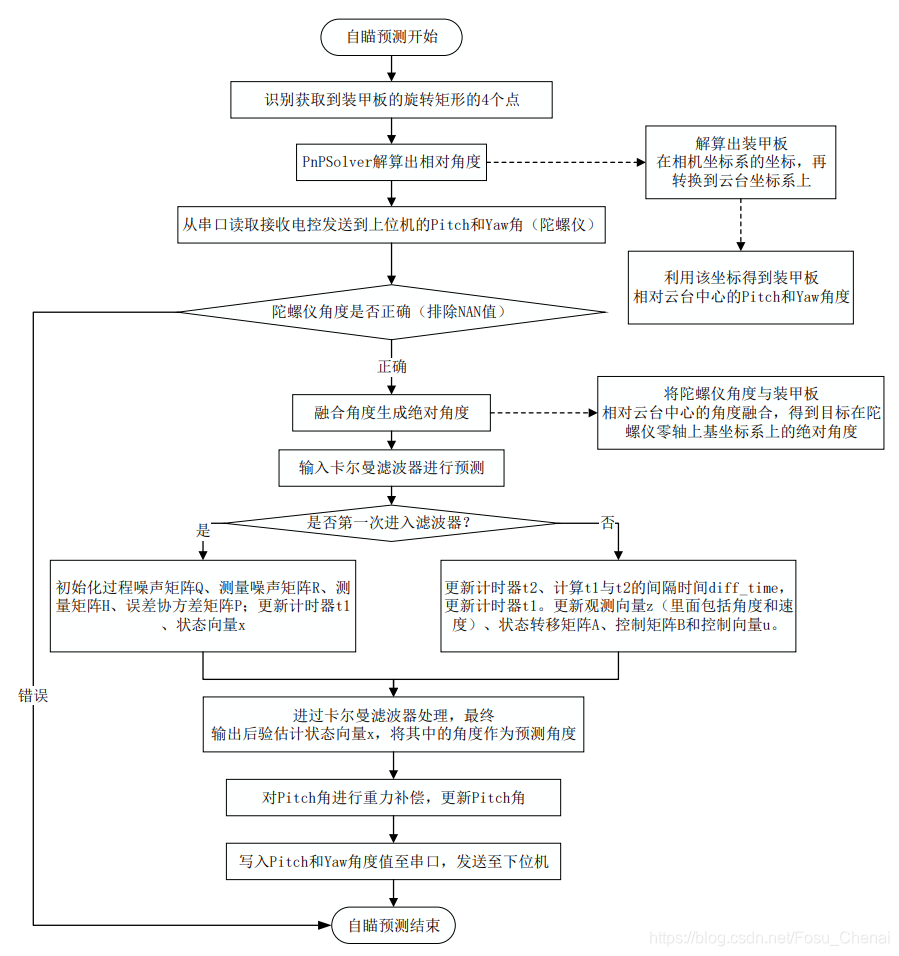
算法流程:
- 1、 识别到装甲板,利用 PnPSolver 算法解算得到目标在相机坐标系的坐标,再转换到机器人云台坐标系上,利用该坐标得到目标相对机器人云台中心的 Pitch 和 Yaw 角度;
- 2、 从串口读取接收电控发送到上位机来的 Pitch 和 Yaw 角(陀螺仪);
- 3、 验证电控角度是否正确(排除 NAN 值);
- 4、 陀螺仪角度与目标相对云台中心的角度融合,得到目标在陀螺仪零轴上基坐标系上的绝对角度;
- 5、 输入卡尔曼滤波器进行预测:
- 5.1、第一次进入:初始化过程噪声矩阵 Q、测量噪声矩阵 R、测量矩阵 H、误差协方差矩阵 P;更新计时器 t1、状态向量 x;
- 5.2、其余时候:更新计时器 t2、计算 t1 与 t2 的间隔时间 diff_time,更新计时器 t1。更新观测向量 z(里面包括角度和速度)、状态转移矩阵 A、控制矩阵 B 和控制向量 u。
- 5.3、每一次最终会输出后验估计状态向量 x,其中的角度信息即作为预测角度;
- 6、重力补偿;
- 7、写入 Pitch 和 Yaw 角度值至串口,发送至下位机。
5.4 自瞄预测流程图
参考文献/文章
[1]卡尔曼滤波算法详细推导
[2]A New Approach to Linear Filtering and Prediction Problems
[3]卡尔曼滤波详解
[4]卡尔曼增益超详细数学推导