Description
形如 1 1 2 3 5 8 13 21 34 55 89 144…的数列,求裴波拉契数列的第n项。
Input
n (1〈 n 〈2^31)
Output
一个数为裴波拉契数列的第n项mod 10000;
Sample Input
123456789
Sample Output
4514
解题思路
矩阵乘法
两个矩阵相乘 A * B,A的行 * B的列 得出新的矩阵C (所以A的列数一定等于B的行数)
![C[i][j] = A[i][k] * B[k][j]](https://img-blog.csdnimg.cn/20201212112715312.png)
那么C的行数等于A的行数,C的列数等于B的列数

考虑构造一个矩阵A
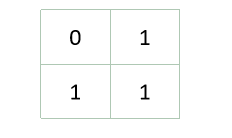
再构造一个矩阵B

那么两个矩阵相乘后得
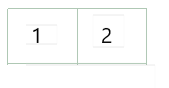
f [ n ] = f [ n − 1 ] + f [ n − 2 ] f[n] = f[n - 1] + f[n - 2] f[n]=f[n−1]+f[n−2]
A = A = A= {
0 , 1 , 1 , 1 0, 1, 1, 1 0,1,1,1}
B = B = B= {
f [ n − 2 ] , f [ n − 1 ] f[n - 2], f[n - 1] f[n−2],f[n−1]}
A ∗ B = A * B = A∗B= { f [ n − 2 ] ∗ 0 + f [ n − 1 ] ∗ 1 , f [ n − 2 ] ∗ 1 + f [ n − 1 ] ∗ 1 f[n - 2] * 0 + f[n - 1] * 1, f[n - 2] * 1 + f[n - 1] * 1 f[n−2]∗0+f[n−1]∗1,f[n−2]∗1+f[n−1]∗1} = = = { f [ n − 1 ] , f [ n ] f[n - 1], f[n] f[n−1],f[n]}
那么答案就等于 B * A * A * A…, 做一个矩阵快速幂把 A n − 1 A^{n-1} An−1算出来再乘上B
Code
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int Mod = 10000;
long long n;
struct DT{
int n, m;
int aed[5][5];
}A, B, Ac;
DT operator *(DT a, DT b){
//矩阵乘法
DT c;
c.n = a.n, c.m = b.m;
memset (c.aed, 0, sizeof (c.aed));
for (int k = 1; k <= a.m; k++)
for (int i = 1; i <= c.n; i++)
for (int j = 1; j <= c.m; j++)
c.aed[i][j] = (c.aed[i][j] + a.aed[i][k] * b.aed[k][j] % Mod) % Mod;
return c;
}
void power (long long n){
//快速幂
if (n == 1)
{
Ac = A;
return;
}
power (n / 2);
Ac = Ac * Ac;
if (n % 2) Ac = Ac * A;
}
int main(){
A.n = A.m = 2;
A.aed[1][2] = A.aed[2][1] = A.aed[2][2] = 1;
B.n = 1, B.m = 2;
B.aed[1][1] = B.aed[1][2] = 1;
scanf ("%lld", &n);
power (n - 1);
B = B * Ac;
printf ("%d", B.aed[1][1]);
}