前言
考试题型
- 简答题(每题5分,共55分)
- 分析题(每题10分,共30分)
- 论述题(15分)
第1章 绪论
- 什么是运动控制系统?
- 运动控制的定义:控制负载的机械运动
- 例子:喷墨打印机
- 负载:墨盒
- 目标:使墨盒在纸面上高速、高精度地来回移动
- 运动控制系统的任务是什么?
- 运动控制系统的组成
- 一个复杂、高速、高精度的多轴协调运动控制是由一种被称为运动控制器的特殊计算机来实现的。
- 一个完整的运动控制系统由以下几个部分组成:
- 人机接口
- 运动控制器。
- 驱动器
- 执行器
- 传动机构
- 反馈


第2章 运动曲线
2.0 引言
- 运动曲线(定义)
- 当某个机械的轴被要求从点 A 移动到点 B时,需要生成这两点之间的连接轨迹
- 在运动控制中,这条轨迹被称为运动曲线
- 工业运动控制的运动曲线(位置、速度、加速度
- 加 速 → 匀 速 → 减 速 加速 \to 匀速 \to 减速 加速→匀速→减速
- 将物体以一个平滑的加速从位置点 A 出发
- 进入匀速运行状态一段时间
- 以一个平滑的减速到达位置点 B 停止


2.1 运动学的基本概念
- 运动学
- 定义:专门描述物体的运动,即物体在空间中的位置随时间的演变而做的改变,完全不考虑作用力或质量等影响运动的因素
- 研究内容:时间 t、位置 s、速度 v 和加速度 a 之间的关系
- 工业运动控制中研究运动学的意义
- 计算运动曲线: s = f ( t , v , a ) s=f(t,v,a) s=f(t,v,a)
- 在机械设计过程中正确选择各轴对应的电机
- 运动曲线的几何规则
- 任意一个函数的积分
- 等于函数曲线在无穷小区间函数值的和
- 即:等于函数曲线下的面积
- s = ∫ v ( t ) d t s=\int v(t)dt s=∫v(t)dt
- t 时刻的位置 s = 直到时刻 t 的速度曲线 v(t) 下的面积
- v = ∫ a ( t ) d t v=\int a(t)dt v=∫a(t)dt
- 加速度是速度曲线的斜率

2.2 常见运动曲线
2.2.1 梯形速度曲线
- 优点:简单
- 缺点:梯形的尖角导致加速度不连续,这将对系统引发较大的冲击
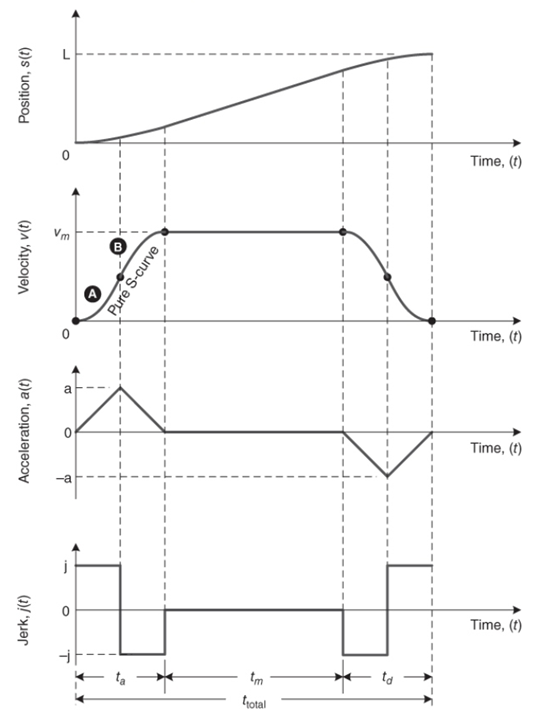
2.2.2 S 形速度曲线
- 为了使加速度平滑连续,可将速度曲线的尖角圆滑处理为 S 形
- S 形速度曲线含有 7 个不同区间
- 其中 4 段用二次方程表达(二次曲线)
- 剩余 3 段是斜率为正、零、负的直线

- 工程简化方法:省略速度曲线的直线段
- 纯 S 形速度曲线由两段二次曲线组成(A、B段)
- 每段可用如下方程表示
- v ( t ) = C 1 t 2 + C 2 t + C 3 v(t)=C_{1}t^2+C_{2}t^+C_{3} v(t)=C1t2+C2t+C3
- C 1 , C 2 , C 3 C_{1}, C_{2}, C_{3} C1,C2,C3是由边界条件决定的系数
第3章 传动链设计
- 传动机构的效率
- 定义:输出功率和输入功率的比值
- 物理意义:摩擦和发热会造成一些输入功率的损失
- 总惯量
- 在轴设计中,如果采用传动机构,将会有部分惯量加在电机轴上,另部分惯量加在负载轴上,此外还有电机(转子)自身的惯量
- 一种通用方法是将所有惯量折算到电机轴上,即总惯量。
- 在电机轴上的总惯量: J t o t a l = J m + J o m + J r e f J_{total}=J_{m}+J_{om}+J_{ref} Jtotal=Jm+Jom+Jref
- J o m J_{om} Jom:直接加在电机轴上的总外加惯量
- J r e f J_{ref} Jref:折算到电机轴上的总惯量

- 上图所示系统用原理示意图的形式画出
- 图中所示元素与方程各项是一一对应的
- 注意在齿轮箱的输出侧(2号轴)总惯量要折算到齿轮箱的输入侧(1号轴)









