2020-04-14 5.2典型环节频率特性
5.1 频率特性的基本概念
- 将其与输入信号相比有:
A ( ω ) = ∣ G ( j ω ) ∣ , 幅 值 比 φ ( ω ) = ∠ G ( j ω ) , 相 角 差 A(\omega)=|G(j\omega)|, 幅值比\\ \varphi(\omega)=\angle G(j\omega), 相角差 A(ω)=∣G(jω)∣,幅值比φ(ω)=∠G(jω),相角差 - 故:对于稳定的线性定常系统
- 由谐波输入产生的输出稳态分量仍然是与输入同频率的谐波函数;
- 而幅值和相角的变化是频率 ω \omega ω的函数,且与系统的传递函数有关。
5.1.1 频率特性的定义
- 正弦波输入下,输出响应中与输入同频率的谐波分量与谐波输入的
- 幅值之比为幅频特性
- 相位之比为相频特性
- 并称其指数表达形式
G ( j ω ) = A ( ω ) e j φ ( ω ) G(j\omega)=A(\omega)e^{j\varphi (\omega)} G(jω)=A(ω)ejφ(ω)
为系统的频率特性。
5.1.2 频率特性的数学表示方法
5.1.2.1 复数形式

5.1.2.2 指数形式

5.1.2.3 对数形式

5.1.3 频率特性的几何表示方法
5.1.3.1 幅相频率特性曲线(Nyquist曲线)

5.1.3.2 对数频率特性曲线(Bode曲线)

- 对数分度
- 比值相同的间隔相同;
- 没有0,1的左边是从0.1开始到1。
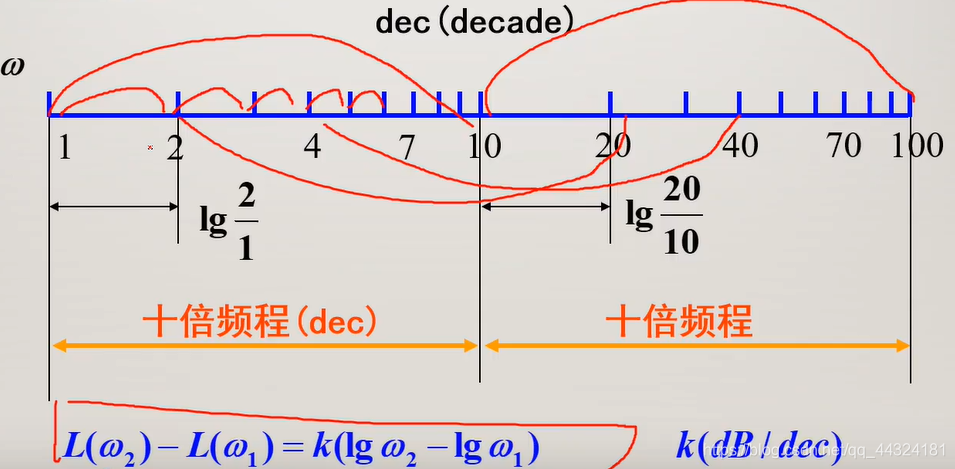
5.2 典型环节与开环系统的频率特性
5.2.1 典型环节


5.2.2 典型环节的频率特性
5.2.2.1 比例环节
G ( j ω ) = K G(j\omega)=K G(jω)=K
L ( ω ) = 20 l g ∣ K ∣ φ ( ω ) = 0 ° L(\omega)=20lg|K|\\ \varphi (\omega)=0° L(ω)=20lg∣K∣φ(ω)=0°
- 左边:Nyquist曲线——为实轴上一个点 ( K , j 0 ) (K, j0) (K,j0)
- 右边:Bode曲线——两条水平线

5.2.2.2 积分环节
G ( j ω ) = 1 j ω ∣ G ( j ω ) ∣ = 1 ω ∠ G ( j ω ) = a r c t a n ( − ∞ ) = − 90 ° G(j\omega)=\frac{1}{j\omega}\\ |G(j\omega)|=\frac{1}{\omega}\\ \angle G(j\omega)=arctan(-\infty)=-90° G(jω)=jω1∣G(jω)∣=ω1∠G(jω)=arctan(−∞)=−90°
L ( ω ) = 20 l g ∣ G ( j ω ) ∣ = 20 l g 1 ω = − 20 l g ω φ ( ω ) = ∠ G ( j ω ) = − 90 ° L(\omega)=20lg|G(j \omega)|=20lg\frac{1}{\omega}=-20lg\omega\\ \varphi (\omega)=\angle G(j\omega)=-90° L(ω)=20lg∣G(jω)∣=20lgω1=−20lgωφ(ω)=∠G(jω)=−90°
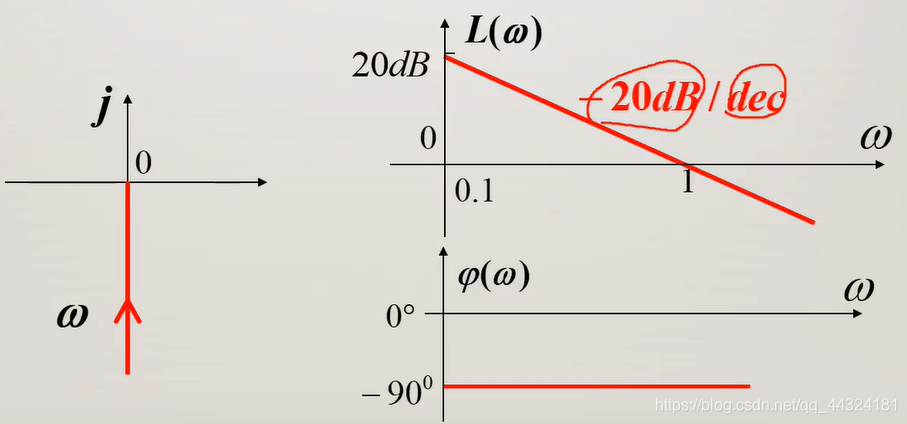
- Nyquist曲线(左边)——在虚轴负半轴上,从无穷远处至原点
G ( j ω ) = 0 − 1 ω ⋅ j G(j\omega)=0-\frac{1}{\omega}\cdot j G(jω)=0−ω1⋅j - Bode曲线(右边)
- 相频特性曲线:一直保持 − 90 ° -90° −90°
- 幅频特性曲线:一条斜率为 − 20 d B / d e c -20dB/dec −20dB/dec的一条斜线,过 ( 1 r a d / s , 0 d B ) (1 rad/s, 0dB) (1rad/s,0dB)这个点
5.2.2.3 微分环节
G ( s ) = s G ( j ω ) = j ω = 0 + ω ⋅ j G(s)=s\\ G(j \omega)=j \omega = 0+\omega \cdot j G(s)=sG(jω)=jω=0+ω⋅j
- Nyquist曲线(左边):从原点出发,虚轴正半轴的射线。
∣ G ( j ω ) ∣ = 0 2 + ω 2 = ω ∠ G ( j ω ) = a r c t a n ( ω 0 ) = a r c t a n ∞ = 90 ° |G(j \omega)| = \sqrt{0^2+\omega^2}=\omega\\ \angle G(j\omega)=arctan(\frac{\omega}{0})=arctan \infty=90° ∣G(jω)∣=02+ω2=ω∠G(jω)=arctan(0ω)=arctan∞=90°
L ( ω ) = 20 l g ∣ G ( j ω ) ∣ = 20 l g ω φ ( ω ) = ∠ G ( j ω ) = 90 ° L(\omega)=20lg|G(j \omega)|=20lg\omega\\ \varphi (\omega)=\angle G(j\omega)=90° L(ω)=20lg∣G(jω)∣=20lgωφ(ω)=∠G(jω)=90°
- Bode曲线(右边)

5.2.2.4 惯性环节
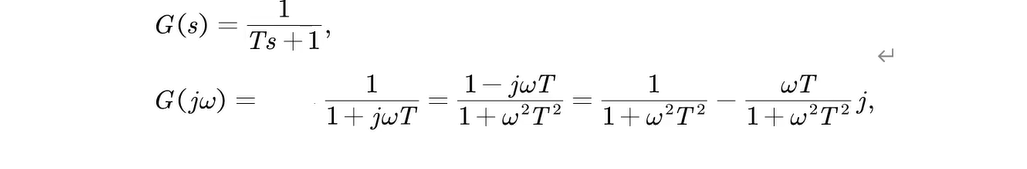
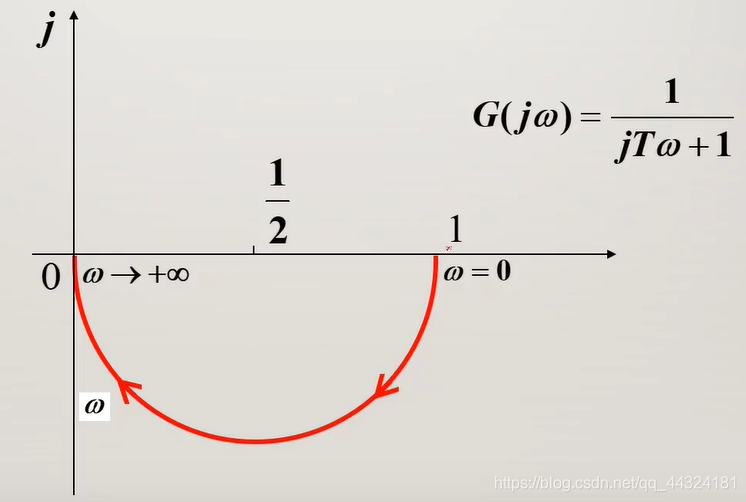
- Nyquist曲线
- 起于 ( 1 , j 0 ) (1, j0) (1,j0),终于原点
- 实部永为正,虚部永为负
- 一直在第四象限
- 是一个半圆
- Bode图
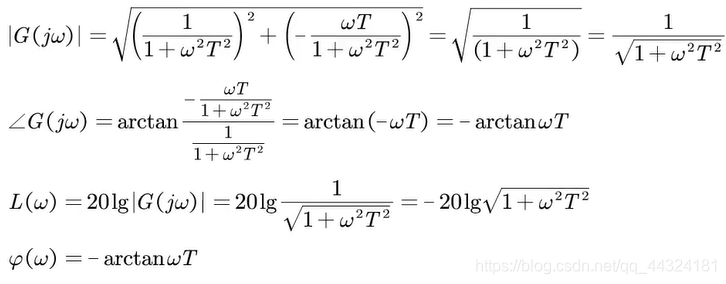
- 幅频特性近似为:
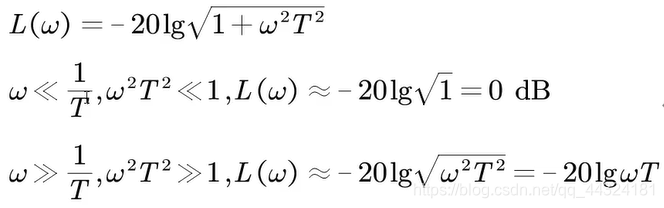
即:
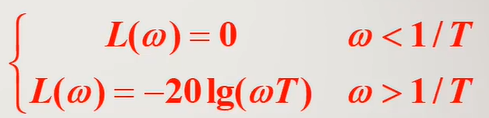
- 幅频特性近似为:
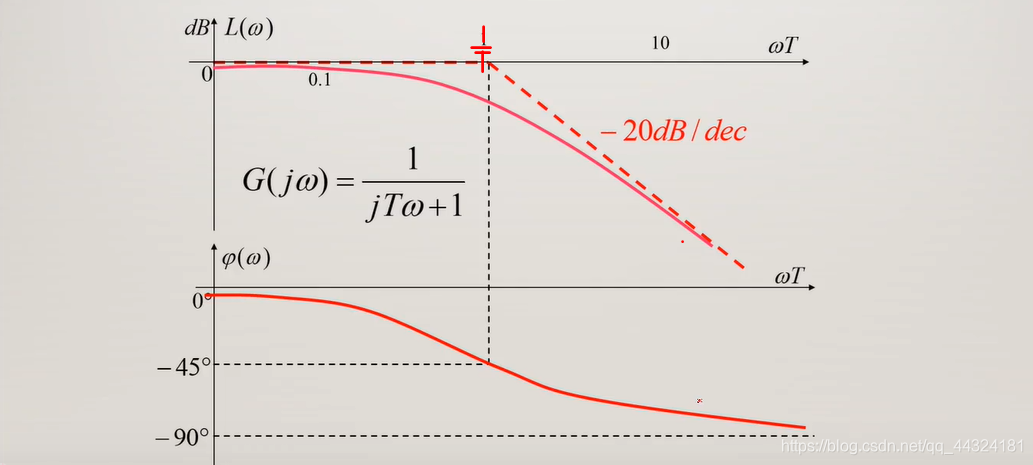
- Bode曲线
- 幅频特性曲线:
- 1 T \frac{1}{T} T1之前是 0 d B 0dB 0dB
- 1 T \frac{1}{T} T1之后是斜率为 − 20 d B / d e c -20dB/dec −20dB/dec的一条直线
- 相频特性曲线:
- 范围是 0 ∼ − 90 ° 0\sim -90° 0∼−90°
- 当 ω = 1 T \omega=\frac{1}{T} ω=T1,输入与输出的相角之差为 − 45 ° -45° −45°
- 幅频特性曲线:
5.2.2.5 一阶微分环节
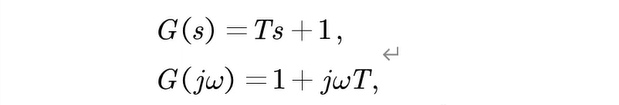
- Nyquist曲线
- 起于 ( 1 , j 0 ) (1, j0) (1,j0),竖直向上的射线

- 起于 ( 1 , j 0 ) (1, j0) (1,j0),竖直向上的射线
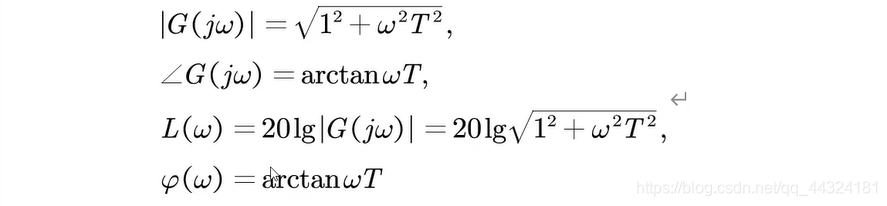
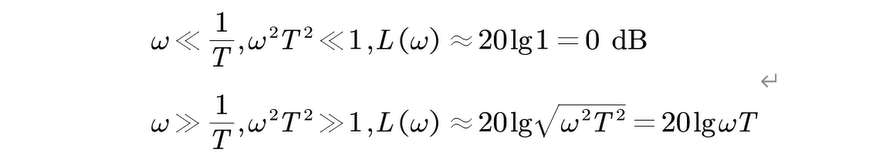
- Bode曲线
- 幅频特性曲线:
- 1 T \frac{1}{T} T1之前是 0 d B 0dB 0dB
- 1 T \frac{1}{T} T1之后是斜率为 + 20 d B / d e c +20dB/dec +20dB/dec的一条直线
- 相频特性曲线:
- 范围是 0 ∼ + 90 ° 0\sim +90° 0∼+90°
- 当 ω = 1 T \omega=\frac{1}{T} ω=T1,输入与输出的相角之差为 + 45 ° +45° +45°
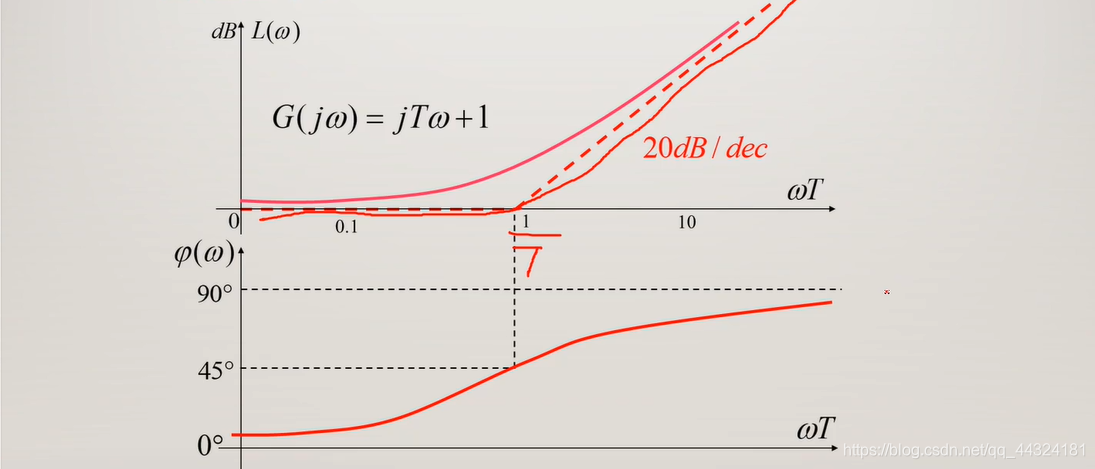
- 幅频特性曲线:
5.2.2.6 振荡环节

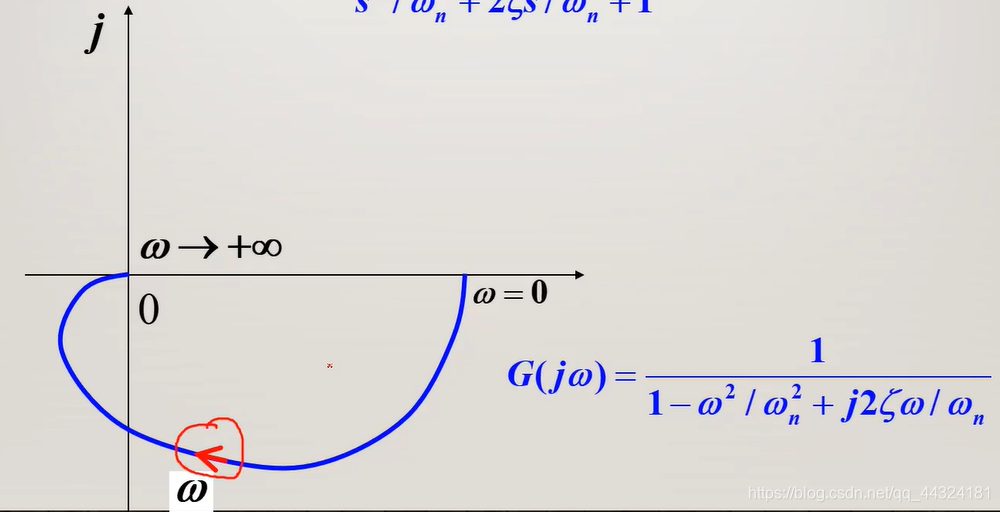
- Nyquist曲线
- 起于 ( 1 , j 0 ) (1, j0) (1,j0)点
- 终于原点
- 虚部永为负
- 实部先正后负,最后趋于0
- 在第三、四象限

- Bode图
- 相角的范围是 0 ° ∼ − 180 ° 0° \sim -180° 0°∼−180°
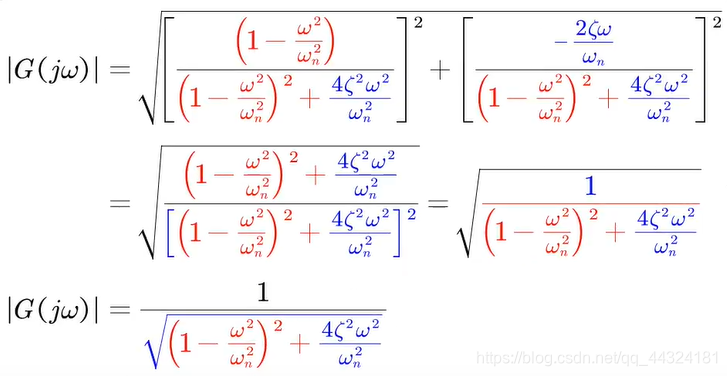
- 对数幅频特性为:

- 渐进特性为:
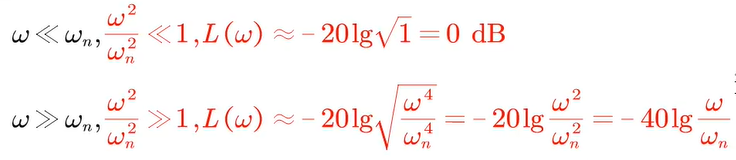
- 幅频特性曲线:
- ω n \omega_{n} ωn之前是 0 d B 0dB 0dB
- ω n \omega_{n} ωn之后是斜率为 − 40 d B / d e c -40dB/dec −40dB/dec的一条直线
- 相频特性曲线:
- 范围是 0 ∼ − 180 ° 0\sim -180° 0∼−180°
- 当 ω = ω n \omega=\omega_{n} ω=ωn,输入与输出的相角之差为 − 90 ° -90° −90°

5.2.2.7 二阶微分环节
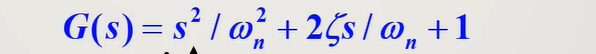
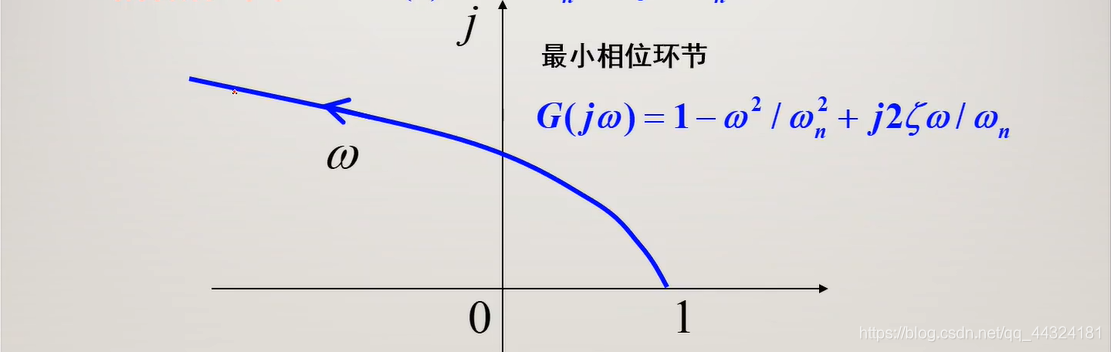
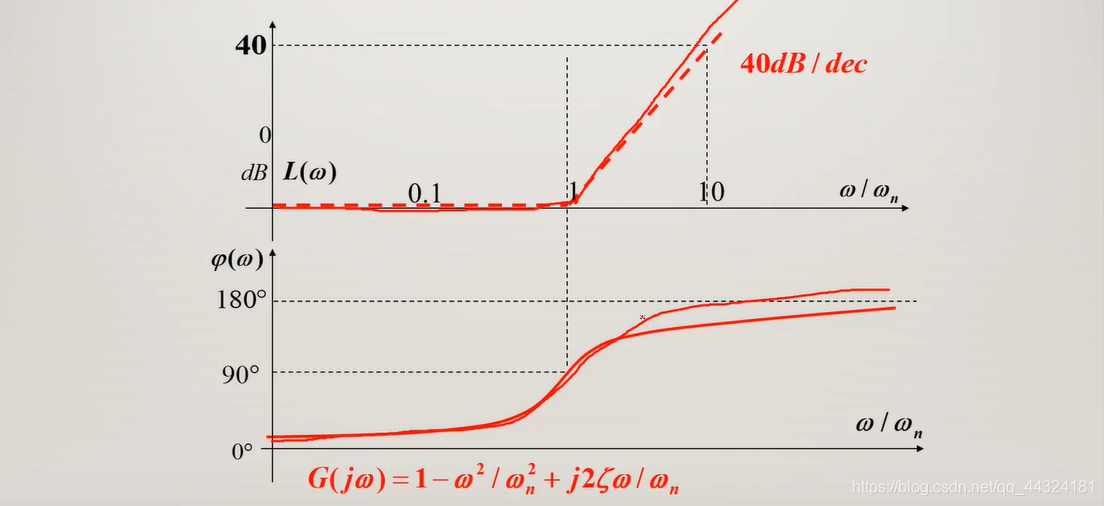
5.2.2.5 总结规律
- 传递函数互为倒数的典型环节
- 对数幅频符号相反,关于零dB线对称;
- 对数相频符号相反,关于零度线对称。
下一篇:开环系统Nyquist曲线绘制