一篇就能搞懂堆
目录
1 概念
1.1 初印象
大根堆
小根堆
堆排序
堆(JVM)
1kw 个数,快速找出前10个
队列 优先级高的先执行
上面的概念 和 解决的场景 有所听过吧(听过就行了,看完这篇文章你就能了解原理了),对的,堆就可以解决上述问题。
1.2 前提
二进制计算:第N为之前的2^1+2^2+…+2^(N-1)值之和为 2^N-1 (体会下:二进制11再加1就是100)
完全二叉树
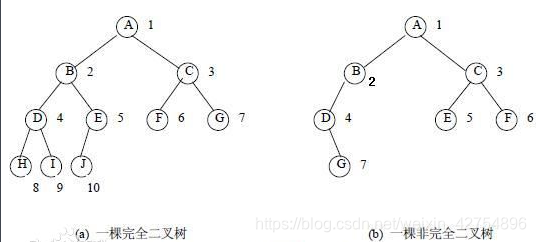
链表,数组
1.3 认识堆

- 堆 必须是完全二叉树
- 堆 分为 大根堆 & 小根堆
- 大根堆:父节点值比子节点值大
- 小根堆:父节点值比子节点值小
- 兄弟节点之间值 无所谓
- 对摆放顺序 是一层一层,从左到右
- 一般使用数组实现,链表实现的二叉树,分层操作复杂且很浪费空间
- 堆 只能 确保只有一个最大数或者最小数,排队第二的不清楚
1.4 堆树对比
- 堆 同二叉搜索树 一样是一种 满足某种特性的 二叉树 树结构
- 特性:堆只不过对是 父节点大于左右子树;二叉搜索树 是左子树<根<右子树。
- 存储:树可以用链表实现,也可以用数组。二叉查找树更侧重搜索效率,常使用链表实现。堆则更注重最大值的获取,是完全二叉树,按层操作二叉树,如果使用链表将使得操作很复杂,使用数组存储对,关系可以使用数组下标计算得出,不用外余存储子节点应用,更节约空间。
- 平衡:二叉搜索树 只有在平衡的时候 搜索复杂度才是O(log n),一般的二叉查找树在不好的情况下就是一个链表,复杂度为O(n)。堆是完全二叉树,当然平衡,搜索复杂度当然就满足O(log n)。
- 搜索:平衡二叉查找树就是为搜索而生的;堆中搜索则交慢,更侧重最大值的获取上。
2 堆研究
2.1 存储
要存储树,需要存储两个维度信息:1. 节点本书数据;2. 节点直接的关系。
使用链表存储好处是,数据直接存储,关系使用引用。
如果使用数组,如果每一个元素当做树的一个节点,数据直接存储即可,节点直接关系怎么存储呢?
数组还有啥信息可用呢? 下标,即:元素位置。
如果我告诉你 辈分最高在前,同辈中岁数大的在前,每家最多两个儿子。那么我给你位置编号,你能知道这是谁家的儿子吗?
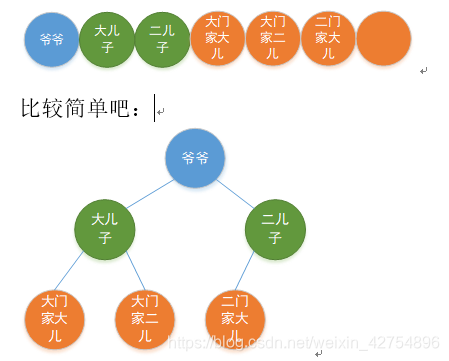
存储:
数据:节点数据放在数组中,i为数组下标。
关系:
父à子:2i+1 & 2i+2 (i为某节点的小标)
子à父:(i-1)/2 (i是子节点下标,/是整除意思)
举例:
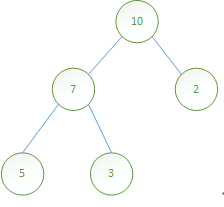
数组:[ 10, 7, 2, 5, 1 ]
根据上述公式计算得:
Node ArrayIndex(i) ParentIndex LeftChild RightChild
10 0 0 1 2
7 1 0 3 4
2 2 0 5(×) 6(×)
5 3 1 7(×) 8(×)
1 4 1 9(×) 10(×)
2.2 父子大小
父节点-->子节点: (i 为父节点下标)
大根堆:父节点 > 子节点
Array[i] > Array[2i+1]
Array[i] > Array[2i+2]
小根堆:父节点 < 子节点
Array[i] < Array[2i+1]
Array[i] < Array[2i+2]
子节点-->父节点 : (i 为子节点下标)
大根堆:子节点 < 父节点
Array[i] < Array[(i-1)/2]
小根堆:子节点 > 父节点
Array[i] > Array[(i-1)/2]
2.3 下标同层关系
定义层数:从0开始,根节点为第0层。

如果一个堆有 n 个节点,那么它的高度是 h = log2(n)。这是因为我们总是要将这一层完全填满以后才会填充新的一层。上面的例子有 15 个节点,所以它的高度是 floor(log2(15)) = floor(3.91) = 3。
2.4 堆节点数
一个h层的堆,最多有:2^(h+1) - 1 个节点。
每一层的节点个数:2^h
从第一层到第h层节点总数:2^h-1
那么一个具有第h层的堆节点个数 = 2^h + 2^h-1 = 2^(h+1) - 1
2.5 叶子节点数
一个堆叶子节点总数为n,那么叶节点总是位于数组的 n/2 和 n-1 之间。
2.6 操作逻辑
增加
从上到下,从左到右。
每次将增加的节点放在最下层的最右边空位。

添加16

调整对满足属性
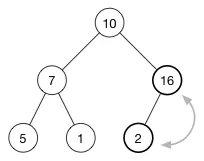
16不用跟兄弟节点7比较了,父节点10>左子节点7,现在右子节点16>父节点,一定也大于兄弟节点。

删除根节点

删除10,现在顶部有一个空的节点,怎么处理?

我们取出数组中的最后一个元素,将它放到树的顶部,然后再修复堆属性。

为了保持最大堆的堆属性,需要调整。

继续堆化直到该节点没有任何子节点或者它比两个子节点都要大为止。

删除任意节点
绝大多数时候你需要删除的是堆的根节点,因为这就是堆的设计用途。
但是,删除任意节点也很有用。

删除 (7),数组中的删除是:我们需要将删除的元素和最后一个元素交换,保证前面的数据都是有用的。
[ 10, 7, 2, 5, 1 ] (有用下标:[0,4])
删除后:
[ 10, 1, 2, 5, 7 ] (有用下标:[0,3])
替换后,

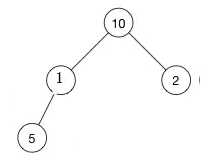
底层节点跑到上面去了,那么就需要调整堆。可能是向下调整了,直到满足属性。
遍历
这就不用说了吧,直接遍历数组即可。
改
就是一次删除和一次增加。
2.7 堆排序
从大到小:
- 大根堆 构建完成后,每次将 根节点输出来,直到没有元素。
- 原理:大根堆每次输出的根是堆中 最大的
从小到大:
- 小根堆同理
3 基本操作
3.1 HeapTest
package com.example.demo;
import org.junit.Before;
import org.junit.Test;
import org.springframework.boot.test.context.SpringBootTest;
import com.example.demo.heap.Heap;
@SpringBootTest(classes = HeapApplication.class)
public class HeapTest {
private Heap heap;
@Before
public void init(){
int[] datas = new int[] { 7, 10, 2, 5, 1 };
Heap p = new Heap();
for (int i = 0; i < datas.length; i++) {
// 新增数据
p.add(datas[i]);
}
p.printRelationship();
this.heap = p;
}
@Test
public void add() {
}
@Test
public void delete() {
// 删除任意节点
heap.delete(2);
heap.printRelationship();
}
@Test
public void remove(){
// 移除根节点
System.out.println("移除根节点:" + this.heap.remove());
heap.printRelationship();
}
@Test
public void sort(){
// 将所有根移除,就是堆排序
int temp = -1;
while((temp = heap.remove())!= -1){
System.out.print(temp + " ");
}
}
}
3.2 Heap
package com.example.demo.heap;
/**
* 堆
*/
public class Heap {
// 容量
private int capcity = 16;
// 数组的有效长度
private int size = -1;
// 堆数组
private int[] datas = new int[capcity];
/**
* 判断是否是空堆
* @return
*/
public boolean empty() {
return datas == null || datas.length == 0 || this.size == -1;
}
/**
* 删除 数据
* @param data
*/
public void delete(int data) {
int i = -1;
if ((i = this.queryIndex(data)) == -1) {
System.out.println("没有找到");
return;
}
// 删除数据
System.out.println("删除数据: " + this.datas[i]);
// 使用最后那个补充
this.datas[i] = this.datas[this.size--];
// 向下调整
this.shiftDown(i);
}
// 检索数据并返回下标
private int queryIndex(int data) {
if (this.empty()) {
return -1;
}
for (int i = 0; i <= this.size; i++) {
if (this.datas[i] == data) {
return i;
}
}
return -1;
}
/**
* 移除根元素
*
* @return
*/
public int remove() {
if (this.size == -1) {
return -1;
}
// 获取根节点
int root = this.datas[0];
// 将最后面的节点补在根节点
this.datas[0] = this.datas[this.size--];
// 向下调整
this.shiftDown(0);
return root;
}
/**
* 添加数据
*
* @param data
* @return
*/
public int[] add(int data) {
// 判断容量
if (size == capcity) {
System.out.println("容量不足");
}
// 存储数据
datas[++size] = data;
// 第一个没必要调整属性
if (size != 0) {
this.shiftUp(this.size);
}
return this.datas;
}
// 向下比较
private void shiftDown(int pi) {
// 如果是叶子节点就没必要在比较了
if (pi > this.size) {
return;
}
// 获取两个子节点Index
int ci1 = this.getFirstChildIndex(pi);
int ci2 = ci1 + 1;
/*
* 获取 需要替换的子节点
* 1. 没有子节点了,即:ci1和ci2 都在size外了
* 2. 有一个子节点, 那也只能是1了
* 3. 有两个子节点,选出比较大的那个
*/
if (ci1 > this.size) {
/*
* && ci2 > this.size 没必要了吧,ci2 = ci1+1 没有子节点了,该节点已经在最底层了
*/
return;
} else if (ci1 == this.size) {
/*
* && ci2 一定大于size了
*/
if (this.datas[ci1] > this.datas[pi]) {
this.exchangeData(ci1, pi);
// 替换后直接返回,没必要在下午了。
return;
}
} else if (ci2 <= this.size) {
/*
* c1 也一定 < this.size了
*/
int mi = this.maxIndex(ci1, ci2);
if (this.datas[mi] > this.datas[pi]) {
// 子节点中 最大的 还大于 目标节点,则替换后
this.exchangeData(mi, pi);
// 继续
this.shiftDown(mi);
}
}
}
// 向上比较
private void shiftUp(int ci) {
// 如果目标节点下标是0,则是根节点,不需要比较了
if (ci == 0) {
return;
}
int pi = this.getParentIndex(ci);
// 子节点的 还比 父节点 大,说明 还需要向上走
if (this.datas[pi] < this.datas[ci]) {
// 换值
this.exchangeData(pi, ci);
// 换完后 pi成为 目标节点 index,继续shiftup
this.shiftUp(pi);
}
// 其他的则不作处理
}
// 中间变量
private int temp;
// 跟换数组的值
private void exchangeData(int x, int y) {
this.temp = this.datas[x];
this.datas[x] = this.datas[y];
this.datas[y] = this.temp;
}
// 获取最大值下标
private int maxIndex(int x, int y) {
return this.datas[x] > this.datas[y] ? x : y;
}
/**
* 打印推的关系
*/
public void printRelationship() {
if (datas == null || datas.length == 0 || this.size == -1) {
System.out.println("空堆");
return;
}
System.out.println(String.format(
"%5s %10s %10s %10s %10s", "Node",
"ArrayIndex(i)",
"ParentIndex",
"LeftChild",
"RightChild"));
for (int i = 0; i <= this.size; i++) {
System.out.println(String.format("%5s %10s %10s %10s %10s",
datas[i], i,
this.checkIndex(this.getParentIndex(i)),
this.checkIndex(this.getFirstChildIndex(i)),
this.checkIndex(this.getFirstChildIndex(i) + 1)));
}
}
// 检查index
private String checkIndex(int i) {
if (i > this.size) {
return "×";
}
return i + "";
}
// 获取 第一个子节点的下标
private int getFirstChildIndex(int parentIndex) {
return parentIndex * 2 + 1;
}
// 获取 父节点的 下标
private int getParentIndex(int childIndex) {
return (childIndex - 1) / 2;
}
}
4 附录
4.1 父子关系推导

4.2 参考1:
https://www.jianshu.com/p/6b526aa481b1
大道至简。