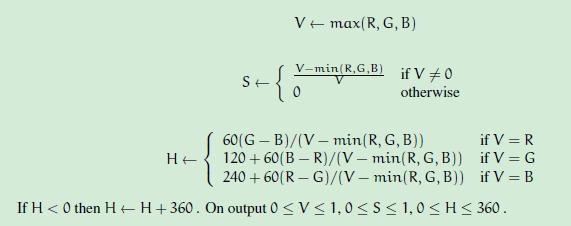RGB颜色空间转换HSV颜色空间 RGB2HSV算法

这是最常用的RGB到HSV例程，还有一个额外的小优化（向除数添加1e-20f以避免需要将除法除以零）：

讲解：——————————————action————————————————

直接看这段代码很有可能会不知所云。首先要理解HSV颜色空间与RGB颜色空间的转换原理。查找相关资料后并不难理解。这里贴出一张最终计算公式。

上述代码就是围绕这个计算公式进行的。

1.首先计算出RGB的最大和最小通道值

2.计算delta差值

3.直接计算S V通道值

4.首先根据下面公式直接翻译代码（1.0f对应60°）

讲解：——————————————end—————————————————

有几件事情值得注意：

                                                                                         图3

讲解：——————————————action————————————————

直接看图1。当时蒙圈了。仔细分析后发现只是将H<0的时候的情况拆开了。

例如V=R时。G和B的关系并不确定。但我们公式中是（G-B）这个我们希望保持不变。

因此当G>B时公式不变

B>R时 公式结构不变。但符号明显是负的，只需加上6.0f（即360°）

图2 图3也就迎刃而解

讲解：——————————————end—————————————————

这实际上是相同的计算！只有色调偏移K会发生变化。现在的想法如下：

将这个想法付诸实践为我们提供了以下代码

讲解：——————————————action—————————————————

通过上述。我们知道，最终目的是构建一个K值，用了解最终的H颜色通道是加上多少数值，确保在（0-360°）空间内

这段代码具体为什么这样书写，由于能力有限是在难以理解，但带入各个值进去，最终结果都是正确的

讲解：——————————————end——————————————————

您可以自己检查上面显示的K值是否由该函数正确生成。还有许多其他方法可以对（r，g，b）进行排序，但是这个特定方法可以让我们进行最后一次优化。

我们注意到，在过去的交换有效地改变的迹象ķ 和的符号g ^ - B。由于两者都被添加并传递给fabs（），实际上可以省略符号反转。

额外的tip给了我们这个最终的代码：

这是2次测试和1次std :: min调用，而不是之前的3次测试和4次std :: min / max调用。我们真的应该在这里看到一些性能提升。

正如预期的那样，基准测试表明，各种CPU，编译器和编译器标志的性能提升了25％到40％。下图（每次转换的平均纳秒数）在Core i7-2600K CPU上，使用g ++ 4.7.2 -O3 -ffast-math：

到这。引用大神的短文就分析完了。回过头来说说最初贴出来的代码。

K中分别对应的构建的K值为（0，-120°，240°，-360°）为什么会有负值正值之分我也不是很理解。

p比较出b g通道的大小，然后q比较max(b g)与r通道。

d求出最大最小的差值

hsv返回最终结果

总之，代码能够看懂了。但是这样构建的原理不能理解，为什么将K值放在构建的p q的第三个通道位置即z 而不是w的位置

以及K值为（0，-120°，240°，-360°）为什么会有负值正值之分我也不是很理解。

实际的色调计算取决于r，g和b的排序方式：

                                                  

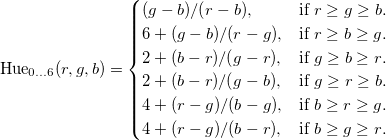
                                                                                         图1

但是让我们用x，y和z来重写它，其中x是（r，g，b）中最大的，z是三者中最小的，y在中间：

                                                   

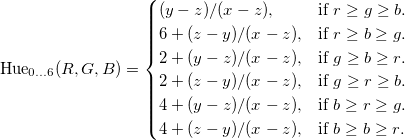
                                                                                         图2

这里有很多相似之处。根据定义，我们可以使用x≥z和y≥z的事实进一步推动它：

                                            

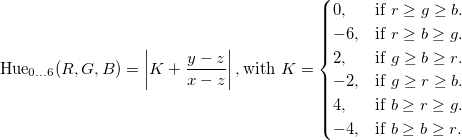
1. vec3 rgb2hsv(vec3 c) {

2. vec4 K = vec4(0.0, -1.0 / 3.0, 2.0 / 3.0, -1.0);

3. vec4 p = mix(vec4(c.bg, K.wz), vec4(c.gb, K.xy), step(c.b, c.g));

4. vec4 q = mix(vec4(p.xyw, c.r), vec4(c.r, p.yzx), step(p.x, c.r));

5. float d = q.x - min(q.w, q.y);

6. float e = 1.0e-10;

7. vec3 hsv = vec3(abs(q.z + (q.w - q.y) / (6.0 * d + e)), d / (q.x + e), q.x);

8. return hsv;

9. }

10. 在stackoverflow找到这样一番回答

    https://stackoverflow.com/questions/15095909/from-rgb-to-hsv-in-opengl-glsl

    其中有一条回复指出了RGB2HSV方法的大致讲解

    http://lolengine.net/blog/2013/07/27/rgb-to-hsv-in-glsl

    下面是引用该文章，并进行分析

    RGB到HSV转换

    该操作通常执行的转换，从RGB到HSV有以下几个步骤：

11. 找到最大的RGB颜色通道
12. 找到最小的RGB颜色通道
13. 计算V和S.
14. 选择H的主循环扇区
15. 计算H.

16. static void RGB2HSV(float r, float g, float b, float &h, float &s, float &v)

17. {

18. float rgb_max = std::max(r, std::max(g, b));

19. float rgb_min = std::min(r, std::min(g, b));

20. float delta = rgb_max - rgb_min;

21. s = delta / (rgb_max + 1e-20f);

22. v = rgb_max;

23.  

24. float hue;

25. if (r == rgb_max)

26. hue = (g - b) / (delta + 1e-20f);

27. else if (g == rgb_max)

28. hue = 2 + (b - r) / (delta + 1e-20f);

29. else

30. hue = 4 + (r - g) / (delta + 1e-20f);

31. if (hue < 0)

32. hue += 6.f;

33. h = hue * (1.f / 6.f);

34. }

35. 大多数复杂性来自色调（Hue）计算。
36. 执行四个最小/最大操作以查找rgb_max和rgb_min; 但是，只需3次比较即可完成三个值的排序。这不一定是有问题的，因为根据CPU，可以以有效的方式连接最小/最大值。
37. 两个额外的测试进行比较r，并g到rgb_max; 如果rgb_max并且rgb_min是使用测试计算的，那么再次比较它们是浪费时间。
38. 将6.f添加到最终的色调值只有16.6％的可能性发生。
39. 使用比较对三元组（r，g，b）进行 排序
40. 在对三元组进行排序时 构建K.
41. 执行最终计算

42. static void RGB2HSV(float r, float g, float b,float &h, float &s, float &v)

43. {

44. float K = 0.f;

45.  

46. if (g < b)

47. {

48. float tmp = g; g = b; b = tmp;

49. K = -1.f;

50. }

51.  

52. if (r < g)

53. {

54. float tmp = r; r = g; g = tmp;

55. K = -2.f / 6.f - K;

56. }

57.  

58. if (g < b)

59. {

60. float tmp = g; g = b; b = tmp;

61. K = -K;

62. }

63.  

64. float chroma = r - b;

65. h = fabs(K + (g - b) / (6.f * chroma + 1e-20f));

66. s = chroma / (r + 1e-20f);

67. v = r;

68. }

69. static void RGB2HSV(float r, float g, float b, float &h, float &s, float &v)

70. {

71. float K = 0.f;

72.  

73. if (g < b)

74. {

75. std::swap(g, b);

76. K = -1.f;

77. }

78.  

79. if (r < g)

80. {

81. std::swap(r, g);

82. K = -2.f / 6.f - K;

83. }

84.  

85. float chroma = r - std::min(g, b);

86. h = fabs(K + (g - b) / (6.f * chroma + 1e-20f));

87. s = chroma / (r + 1e-20f);

88. v = r;

89. }

90. vec3 rgb2hsv(vec3 c) {

91. vec4 K = vec4(0.0, -1.0 / 3.0, 2.0 / 3.0, -1.0);

92. vec4 p = mix(vec4(c.bg, K.wz), vec4(c.gb, K.xy), step(c.b, c.g));

93. vec4 q = mix(vec4(p.xyw, c.r), vec4(c.r, p.yzx), step(p.x, c.r));

94. float d = q.x - min(q.w, q.y);

95. float e = 1.0e-10;

96. vec3 hsv = vec3(abs(q.z + (q.w - q.y) / (6.0 * d + e)), d / (q.x + e), q.x);

97. return hsv;

98. }