本文提出一种新的黑盒对抗攻击方法AdvFlow,通过利用标准化流来建模对抗样本的数据分布,使得生成的对抗样本的分布和正常样本接近,从而让对抗样本更难被检测出来,打破了对抗样本和正常样本的分布大不相同的固有认知。

论文地址:https://arxiv.org/abs/2007.07435
论文代码:https://github.com/hmdolatabadi/AdvFlow
本文为极市原创投稿,转载请获得授权。
引言
虽然神经网络在很多机器学习任务上都取得了非凡的表现,但是通过对输入样本添加微小的扰动,就能使其分类错误(这也就是对抗攻击)。神经网络对对抗攻击的脆弱性,大大限制了它们在现实生活中的广泛应用。因此,设计出有效的对抗攻击方法来模拟现实世界中可能出现的各种威胁,有利于我们不断改进神经网络模型,使得模型对这些攻击更加鲁棒。一般来说,对抗攻击的方法可以分为两大类:白盒攻击和黑盒攻击。在白盒攻击中,攻击者对要攻击的模型(目标模型)了如指掌,比如目标模型的结构,参数等等都可以获得。而在黑盒攻击中,攻击者对目标模型的内部一无所知,只能通过不断询问模型,给定输入,观察模型的输出,来和模型进行互动。因此,黑盒攻击更加贴近现实场景。在本文中,作者提出了一种有效的黑盒攻击方法,借助流模型的思想来建模对抗样本的数据分布,使之接近正常样本,从而生成了更难被检测出来的对抗样本。
论文贡献
该论文的贡献可以总结为以下三点:
-
作者提出了一种新的黑盒攻击方法AdvFlow, 首次将流模型应用到对抗攻击方法中。
-
作者理论上证明了AdvFlow生成的对抗扰动各成分之间具有依赖性,而类似的攻击方法NATTACK [1]则不具有这个性质。
-
AdvFlow生成的对抗样本的数据分布和正常样本接近,从而更难被对抗样本检测器发现。
模型介绍
- 黑盒攻击
给定输入样本 x ∈ X d x\ \in X^{d} x ∈Xd和目标模型 C C C,则 x x x的对抗样本 x adv x_{\text{adv}} xadv可由如下公式生成:
x a d v = arg min x ′ ∈ S ( x ) L ( x ′ ) L ( x ′ ) = max ( 0 , log C ( x ′ ) y − max c ≠ y log C ( x ′ ) c ) S ( x ) = { x ′ ∈ X d ∣ ∥ x ′ − x ∥ p ≤ ϵ max } \begin{array}{c} \mathbf{x}_{a d v}=\underset{\mathbf{x}^{\prime} \in \mathcal{S}(\mathbf{x})}{\arg \min } \mathcal{L}\left(\mathbf{x}^{\prime}\right) \\ \mathcal{L}\left(\mathbf{x}^{\prime}\right)=\max \left(0, \log \mathcal{C}\left(\mathbf{x}^{\prime}\right)_{y}-\max _{c \neq y} \log \mathcal{C}\left(\mathbf{x}^{\prime}\right)_{c}\right) \\ \mathcal{S}(\mathbf{x})=\left\{\mathbf{x}^{\prime} \in \mathcal{X}^{d} \mid\left\|\mathbf{x}^{\prime}-\mathbf{x}\right\|_{p} \leq \epsilon_{\max }\right\} \end{array} xadv=x′∈S(x)argminL(x′)L(x′)=max(0,logC(x′)y−maxc=ylogC(x′)c)S(x)={ x′∈Xd∣∥x′−x∥p≤ϵmax}
这里 C ( x ′ ) y {C(x')}_{y} C(x′)y表示分类器输出的第 y y y个元素, S ( x ) S(x) S(x)表示 x x x的对抗样本的定义域。
- 标准化流(NF)
标准化流(NF)是一种生成模型,目标在于建模给定数据集的概率分布。假设 Z , X ∈ R d Z,\ X \in \mathbb{R}^{d} Z, X∈Rd分别为两个随机向量,从 Z Z Z到 X X X的转换函数为$f:\ \mathbb{R}^{d} \rightarrow \ \mathbb{R}^{d}\ $, f f f可逆并且可微。若已知 Z Z Z的概率分布为 p ( z ) p(z) p(z), 则 X X X的概率分布为:
p ( x ) = p ( z ) ∣ det ( ∂ f ∂ z ) ∣ − 1 p(\mathrm{x})=p(\mathrm{z})\left|\operatorname{det}\left(\frac{\partial \mathrm{f}}{\partial \mathrm{z}}\right)\right|^{-1} p(x)=p(z)∣∣∣∣det(∂z∂f)∣∣∣∣−1
流模型一般使用可逆神经网络(INN)来建模转换函数 f f f,从而得到 X X X的数据分布。在本文中,作者假设随机向量 Z Z Z服从正态分布。
标准化流(NF)利用极大似然估计作为目标函数来训练可逆神经网络(INN)的参数 θ \theta θ,具体公式为:
θ ∗ = arg max θ 1 n ∑ i = 1 n log p θ ( x i ) \boldsymbol{\theta}^{*}=\underset{\boldsymbol{\theta}}{\arg \max } \frac{1}{n} \sum_{i=1}^{n} \log p_{\boldsymbol{\theta}}\left(\mathbf{x}_{i}\right) θ∗=θargmaxn1i=1∑nlogpθ(xi)
- AdvFlow
令 f \text{f\ } f 表示在正常样本上预训练的满足可逆和可微性质的标准化流(NF)模型,则AdvFlow生成对抗样本的公式为:
x ′ = proj S ( f ( z ) ) , z ∼ N ( z ∣ μ , σ 2 I ) \mathbf{x}^{\prime}=\operatorname{proj}_{\mathcal{S}}(\mathbf{f}(\mathbf{z})), \quad \mathbf{z} \sim \mathcal{N}\left(\mathbf{z} \mid \boldsymbol{\mu}, \sigma^{2} I\right) x′=projS(f(z)),z∼N(z∣μ,σ2I)
这里 proj S \text{proj}_{S} projS表示一个映射规则,限制生成的对抗样本在定义域 S ( x ) S(x) S(x)内。 z z z为服从均值为 μ \mu μ,方差为 σ 2 \sigma^{2} σ2的正态分布的随机向量。通过前面介绍的标准化流的思想,我们可知* f ( z ) f(z) f(z)的分布和正常样本的分布接近,从而生成的对抗样本的分布也就接近正常样本。
- AdvFlow生成的对抗扰动的唯一性:
假设 f ( x ) f(x) f(x)为一个可逆并且可微的函数, δ z \delta_{z} δz为一个小的扰动,则有
δ = f ( f − 1 ( x ) + δ z ) − x ≈ ( ∇ f − 1 ( x ) ) − 1 δ z \delta=\mathrm{f}\left(\mathrm{f}^{-1}(\mathrm{x})+\delta_{z}\right)-\mathrm{x} \approx\left(\nabla \mathrm{f}^{-1}(\mathrm{x})\right)^{-1} \delta_{z} δ=f(f−1(x)+δz)−x≈(∇f−1(x))−1δz
作者证明发现AdvFlow生成的对抗扰动各成分之间具有依赖性,而NATTACK生成的对抗扰动各成分之间互相独立。如下图所示,©为正常样本,(b)和(d)分别为AdvFlow和NATTACK生成的对抗样本,(a)和(d)分别为AdvFlow和NATTACK生成的对抗扰动。我们可以发现AdvFlow生成的对抗扰动捕获了原始图片的结构信息,而不仅仅是噪声。

实验结果
- 可检测性
利用预训练好的对抗样本检测器来检测不同方法生成的对抗样本,检测准确率越低,说明生成的对抗样本越难被发现。
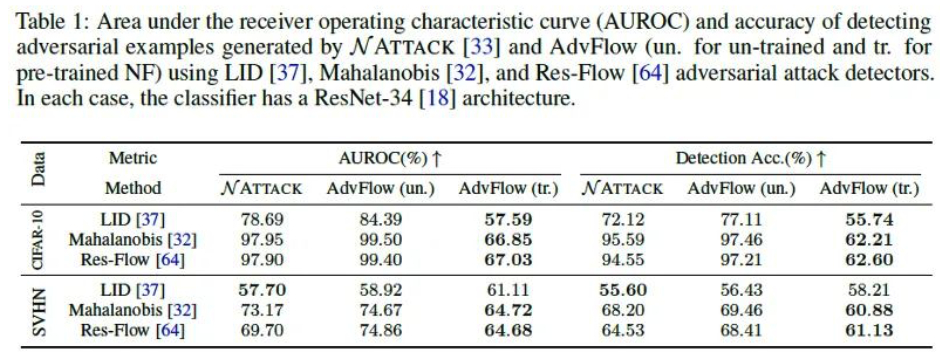
如上表所示,AdvFlow (un.)表示NF模型的权重没有经过预训练,是随机的。AdvFlow (tr.)表示NF模型的权重是预训练好的。相比于NATTACK方法,我们可以看到AdvFlow(tr.)模型生成的对抗样本更难被检测器发现。
此外,如下图所示,我们可以发现AdvFlow生成的对抗样本的分布更加接近原始正常样本的分布,为其更难被检测出来提供了有力的依据。

- 对抗攻击成功率

如上表所示,在四种对抗攻击方法中,AdvFlow的性能基本超越了其他三种方法。
- 迁移性
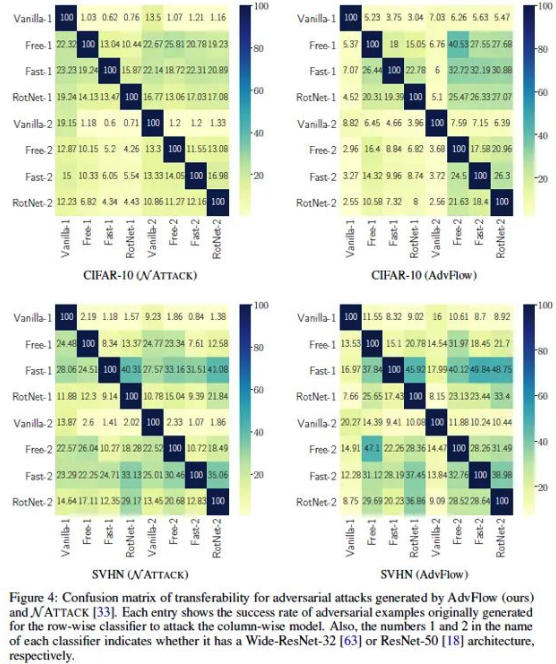
如上图所示,混淆矩阵中每个数值表示用对应行的分类器生成的对抗样本去攻击对应列的分类器所得到的成功率。可以看到,在不同的网络结构和数据集上,AdvFlow比NATTACK具有更好的迁移性。
发展应用
基于本文工作的另一篇工作Black-box Adversarial Example Generation with Normalizing Flows [2]发表在了ICML 2020 Workshop上。为了使AdvFlow算法更快地收敛,该篇论文给出了如下生成对抗样本的流程图。

给定原始输入样本 x x x,预训练的标准化流模型 f ( ⋅ ) f(·) f(⋅),首先将样本 x x x通过 f − 1 ( ⋅ ) f^{- 1}( \cdot ) f−1(⋅)映射为分布空间的表征 z = f − 1 ( x ) z = f^{- 1}(x) z=f−1(x),然后将扰动向量 δ z = μ + σ ϵ \delta_{z} = \mu + \sigma\epsilon δz=μ+σϵ, ϵ ∼ N ( ϵ ∣ 0 , I ) \epsilon\sim N(\epsilon|0,\ I) ϵ∼N(ϵ∣0, I)加到 z z z上得到对抗样本在分布空间的表征 z adv z_{\text{adv}} zadv,最后将 z adv z_{\text{adv}} zadv通过流模型 f ( ⋅ ) f(·) f(⋅)再映射回输入样本空间,得到对抗样本 x adv x_{\text{adv}} xadv。得益于标准化流模型所具有的良好性质(可逆性和可微性),在该种方法中,对抗样本和原始样本在分布空间的表征足够接近,因而生成的对抗样本和原始样本也十分相似。
此外,近几个月,作者在博客中介绍了将AdvFlow应用到高分辨率图像上的方法。由于高分辨率图像需要更大计算开销,为了解决这个问题,作者提出了如下的设计方案:

首先对原始高分辨率图像进行下采样,然后在下采样后的低维空间中,应用AdvFlow生成对抗样本,再计算低维空间中下采样图片和对抗样本之间的差异,将该差异上采样后加到原始的高分辨率图像上,从而得到高分辨率对抗样本,进一步拓宽了AdvFlow的应用场景。
【参考】
[1] Li, Y., Li, L., Wang, L., Zhang, T., and Gong, B. (2019). NATTACK: learning the distributions
of adversarial examples for an improved black-box attack on deep neural networks. In Proceedings
of the 36th International Conference on Machine Learning (ICML), pages 3866–3876
[2] Dolatabadi, H.M., Erfani, S., & Leckie, C. (2020). Black-box Adversarial Example Generation with Normalizing Flows. ArXiv, abs/2007.02734.
[3] https://github.com/hmdolatabadi/AdvFlow
[4] https://hmdolatabadi.github.io/posts/2020/10/advflow
作者东瓠,上海交通大学计算机系硕士研究生在读。欢迎大家联系极市小编(微信ID:fengcall19)加入极市原创作者行列