AtCoder Beginner Contest 181 A-F题解

其他 2021-02-01 10:53:29 阅读次数: 0

我虚拟参加了一下Atcoder新人练习赛181的比赛，比赛中做出了前五题，排170名左右，最后一题没时间了，赛后把最后一题做了一下，也不是很难。
题目链接: https://atcoder.jp/contests/abc181

A - Heavy Rotation

在这里插入图片描述
题意：他现在穿白衣服，一天之后变成黑衣服，再过一天又变成白衣服，依次交替。
思路：就是一个对2取模的问题，直接求解。

#include<iostream>

int main(){
    
    
    int n;
    std::cin>>n;
    if(n%2){
    
    
        std::cout << "Black" << "\n";
    }
    else{
    
    
        std::cout << "White" << "\n";
    }
    return 0;
}

B - Trapezoid Sum

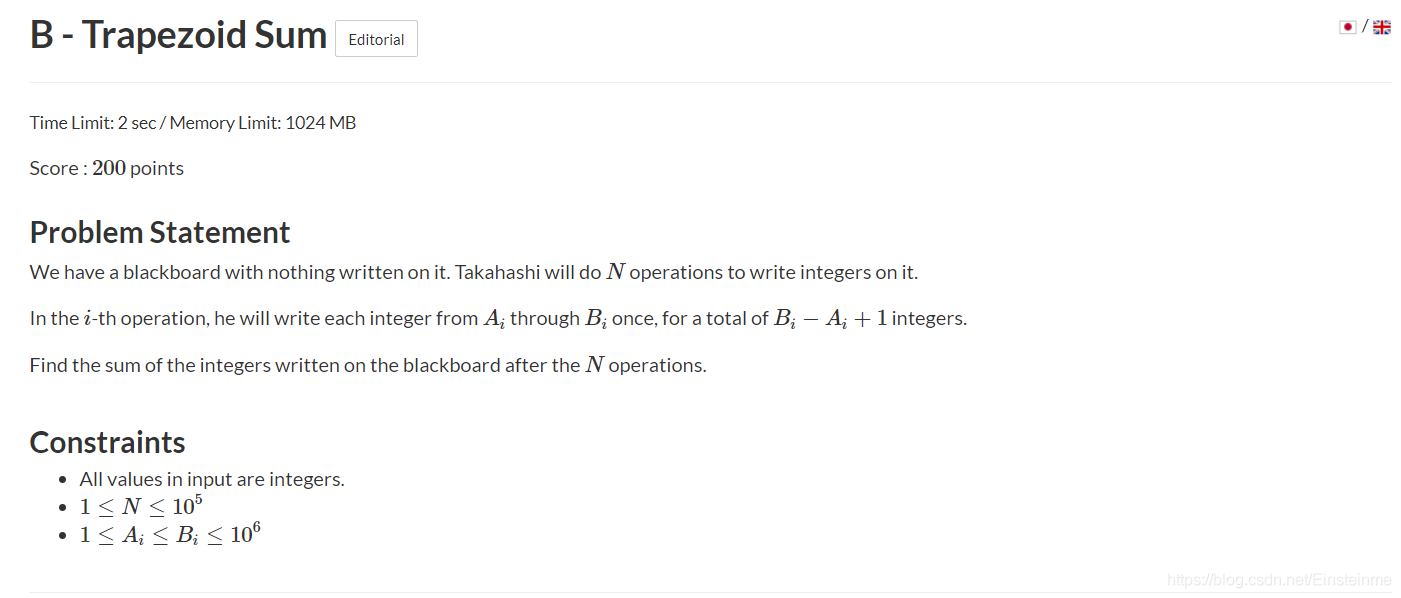
在这里插入图片描述
题意：他每天在黑板上写 A i A_i Ai​到 B i B_i Bi​各一次，问N天后黑板上的数字之和。
思路：每一天写的很多数字是一个等差数列，可以直接用等差数列求和公式 O ( 1 ) O(1) O(1)求出，总的时间复杂度就是 O ( n ) O(n) O(n)。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
int n;

int main(){
    
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    ll ans = 0;
    for(int i = 1; i <= n; i++){
    
    
        ll a, b;
        cin >> a >> b;
        ans += ((a+b)*(b-a+1)/2);
    }
    cout << ans << "\n";
    return 0;
}

C - Collinearity

在这里插入图片描述
题意：让你判断一些点中是否存在三点共线。
思路：三点共线的数学公式：
y 3 − y 1 x 3 − x 1 = y 2 − y 1 x 2 − x 1 \frac{y_3 - y_1}{x_3-x_1} = \frac{y_2-y_1}{x_2-x_1} x3​−x1​y3​−y1​​=x2​−x1​y2​−y1​​
当 x 2 − x 1 ! = 0 a n d x 3 − x 1 ! = 0 x_2 - x_1 !=0 and x_3 - x_1 != 0 x2​−x1​!=0andx3​−x1​!=0
如果 x 2 − x 1 = 0 o r x 3 − x 1 = 0 x_2 - x_1 = 0 or x_3 - x_1 = 0 x2​−x1​=0orx3​−x1​=0
我们可以用叉积公式：
( y 3 − y 1 ) ∗ ( x 2 − x 1 ) = ( y 2 − y 1 ) ∗ ( x 3 − x 1 ) (y_3 - y_1)*(x_2-x_1) = (y_2-y_1)*(x_3-x_1) (y3​−y1​)∗(x2​−x1​)=(y2​−y1​)∗(x3​−x1​)
这样直接模拟即可。

#include<bits/stdc++.h>
using namespace std;

int n;
int x[105];
int y[105];

int main(){
    
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    for(int i = 1; i <= n; i++){
    
    
        cin >> x[i] >> y[i];
    }
    int flag = 0;
    for(int i = 1; i <= n; i++){
    
    
        for(int j = i+1; j <= n; j++){
    
    
            for(int k = j+1; k <= n; k++){
    
    
                if((y[k] - y[i])*(x[j] - x[i]) == (y[j] - y[i])*(x[k] - x[i])){
    
    
                    //cout << i << " " << j << " " << k << "\n";
                    flag = 1;
                    break;
                }
            }
            if(flag){
    
    
                break;
            }
        }
        if(flag){
    
    
            break;
        }
    }
    if(flag){
    
    
        cout << "Yes" << "\n";
    }
    else{
    
    
        cout << "No" << "\n";
    }
    return 0;
}

D - Hachi

在这里插入图片描述
题意：给你一个数字，随意排列，判断是否能被8整除。
思路：一个数被8整除，只要让这个数的后三位被8整除即可。这样，本题可以直接打表过。

#include<bits/stdc++.h>
using namespace std;

string s;
int cnt[15];

bool judge(){
    
    
    if(s.length() == 1){
    
    
        if(cnt[8] == 1 || cnt[0] == 1)
            return true;
        return false;    
    }
    if(s.length() == 2){
    
    
        if(cnt[1] == 1 && cnt[6] == 1)
            return true;
        if(cnt[2] == 1 && cnt[4] == 1)
            return true;
        if(cnt[2] == 1 && cnt[3] == 1)
            return true;
        if(cnt[4] == 1 && cnt[0] == 1)
            return true;
        if(cnt[4] == 1 && cnt[8] == 1)
            return true;
        if(cnt[5] == 1 && cnt[6] == 1)
            return true;
        if(cnt[6] == 1 && cnt[4] == 1)
            return true;
        if(cnt[7] == 1 && cnt[2] == 1)
            return true;
        if(cnt[8] == 1 && cnt[0] == 1)
            return true;
        if(cnt[8] == 2)
            return true;
        if(cnt[9] == 1 && cnt[6] == 1)
            return true;
        return false;                                                
    }
    if(cnt[0] >=2 && cnt[8] >= 1)
        return 1;
    if(cnt[0] >= 1 && cnt[1] >= 1 && cnt[6] >= 1)
        return 1;
    if(cnt[0] >= 1 && cnt[2] >= 1&& cnt[4] >= 1)
        return 1;
    if(cnt[0] >= 1&&cnt[3] >= 1&&cnt[2] >= 1)
        return 1;
    if(cnt[0] >= 2&&cnt[4] >= 1)
        return true;
    if(cnt[0] >= 1 && cnt[4] >= 1 && cnt[8] >= 1)
        return true;
    if(cnt[0] >= 1 && cnt[5] >= 1&&cnt[6] >= 1)
        return true;
    if(cnt[0] >= 1 && cnt[6]>=1&&cnt[4]>=1)
        return true;
    if(cnt[0] >= 1&& cnt[7] >= 1 && cnt[2] >= 1)
        return true;
    if(cnt[0] >= 1 && cnt[8] >= 2)
        return true;    
    if(cnt[0] >= 1 && cnt[9] >= 1 && cnt[6] >= 1)
        return true; 
    if(cnt[1] >=0 &&cnt[0] >=1 && cnt[4] >= 1)
        return 1;
    if(cnt[1] >= 2 && cnt[2] >= 1)
        return 1;
    if(cnt[1] >= 1 && cnt[2] >= 1&& cnt[0] >= 1)
        return 1;
    if(cnt[1] >= 1&&cnt[2] >= 1&&cnt[8] >= 1)
        return 1;
    if(cnt[1] >= 2&&cnt[3] >= 1&&cnt[6]>=1)
        return true;
    if(cnt[1] >= 1 && cnt[4] >= 2)
        return true;
    if(cnt[1] >= 1 && cnt[5] >= 1&&cnt[2] >= 1)
        return true;
    if(cnt[1] >= 1 && cnt[6]>=1&&cnt[0]>=1)
        return true;
    if(cnt[1] >= 1&& cnt[6] >= 1 && cnt[8] >= 1)
        return true;
    if(cnt[1] >= 1 && cnt[7] >= 1 && cnt[6] >= 1)
        return true;    
    if(cnt[1] >= 1 && cnt[8] >= 1 && cnt[4] >= 1)
        return true;                      
    if(cnt[1] >= 1 && cnt[9] >= 1&&cnt[2] >= 1)

    if(cnt[2] >=2 && cnt[0] >= 1)
        return 1;
    if(cnt[2] >= 1 && cnt[0] >= 1 && cnt[8] >= 1)
        return 1;
    if(cnt[2] >= 1 && cnt[1] >= 1&& cnt[6] >= 1)
        return 1;
    if(cnt[2] >= 2&&cnt[4] >= 1)
        return 1;
    if(cnt[2] >= 2&&cnt[3] >= 1)
        return true;
    if(cnt[2] >= 1 && cnt[4] >= 1 && cnt[0] >= 1)
        return true;
    if(cnt[2] >= 1 && cnt[4] >= 1&&cnt[8] >= 1)
        return true;
    if(cnt[2] >= 1 && cnt[5]>=1&&cnt[6]>=1)
        return true;
    if(cnt[2] >= 1&& cnt[6] >= 1 && cnt[4] >= 1)
        return true;
    if(cnt[2] >= 2 && cnt[7] >= 2)
        return true;    
    if(cnt[2] >= 1 && cnt[8] >= 1 && cnt[0] >= 1)
        return true;               
    if(cnt[2] >= 1 && cnt[8] >= 2)
        return true;
    if(cnt[2] >= 1 && cnt[9] >= 1 && cnt[6] >= 1)
        return true;

    if(cnt[3] >=1 && cnt[0] >= 1 && cnt[4] >= 1)
        return 1;
    if(cnt[3] >= 1 && cnt[1] >= 1 && cnt[2] >= 1)
        return 1;
    if(cnt[3] >= 1 && cnt[2] >= 1&& cnt[0] >= 1)
        return 1;
    if(cnt[3] >= 1&&cnt[2] >= 1&&cnt[8] >= 1)
        return 1;
    if(cnt[3] >= 2&&cnt[6] >= 1)
        return true;
    if(cnt[3] >= 1 && cnt[4] >= 2 )
        return true;
    if(cnt[3] >= 1 && cnt[5] >= 1&&cnt[2] >= 1)
        return true;
    if(cnt[3] >= 1 && cnt[6]>=1&&cnt[0]>=1)
        return true;
    if(cnt[3] >= 1&& cnt[6] >= 1 && cnt[8] >= 1)
        return true;
    if(cnt[3] >= 1 && cnt[7] >= 1 && cnt[6] >= 1)
        return true;    
    if(cnt[3] >= 1 && cnt[8] >= 1 && cnt[4] >= 1)
        return true;
    if(cnt[3] >= 1 && cnt[9] >= 1 && cnt[2] >= 1)
        return true;

    if(cnt[0] >=2 && cnt[4] >= 1)
        return 1;
    if(cnt[4] >= 1 && cnt[0] >= 1 && cnt[8] >= 1)
        return 1;
    if(cnt[4] >= 1 && cnt[1] >= 1&& cnt[6] >= 1)
        return 1;
    if(cnt[4] >= 2&&cnt[2] >= 1)
        return 1;
    if(cnt[4] >= 1&&cnt[3] >= 1&&cnt[2] >= 1)
        return true;
    if(cnt[4] >= 2 && cnt[0] >= 1 )
        return true;
    if(cnt[4] >= 2 && cnt[8] >= 1)
        return true;
    if(cnt[4] >= 1 && cnt[5]>=1&&cnt[6]>=1)
        return true;
    if(cnt[4] >= 2&& cnt[6] >= 1 )
        return true;
    if(cnt[4] >= 1 && cnt[7] >= 2 && cnt[2] >= 1)
        return true;    
    if(cnt[4] >= 1 && cnt[8] >= 1 && cnt[0] >= 1)
        return true;                  
    if(cnt[4] >= 1 && cnt[8] >= 2)
        return true;
    if(cnt[4] >= 1 && cnt[9] >= 1 && cnt[6] >= 1)
        return true;

    
    if(cnt[5] >=1 && cnt[0] >= 1 && cnt[4] >= 1)
        return 1;
    if(cnt[5] >= 1 && cnt[1] >= 1 && cnt[2] >= 1)
        return 1;
    if(cnt[5] >= 1 && cnt[2] >= 1&& cnt[0] >= 1)
        return 1;
    if(cnt[5] >= 1&&cnt[2] >= 1&&cnt[8] >= 1)
        return 1;
    if(cnt[5] >= 1&&cnt[3]>=1&&cnt[6] >= 1)
        return true;
    if(cnt[5] >= 1 && cnt[4] >= 2 )
        return true;
    if(cnt[5] >= 2 &&cnt[2] >= 1)
        return true;
    if(cnt[5] >= 1 && cnt[6]>=1&&cnt[0]>=1)
        return true;
    if(cnt[5] >= 1&& cnt[6] >= 1 && cnt[8] >= 1)
        return true;
    if(cnt[5] >= 1 && cnt[7] >= 1 && cnt[6] >= 1)
        return true;    
    if(cnt[5] >= 1 && cnt[8] >= 1 && cnt[4] >= 1)
        return true;
    if(cnt[5] >= 1 && cnt[9] >= 1 && cnt[2] >= 1)
        return true;     

    if(cnt[0] >=2 && cnt[6] >= 1)
        return 1;
    if(cnt[6] >= 1 && cnt[0] >= 1 && cnt[8] >= 1)
        return 1;
    if(cnt[6] >= 2 && cnt[1] >= 1)
        return 1;
    if(cnt[6] >= 1&&cnt[2] >= 1&&cnt[4]>=1)
        return 1;
    if(cnt[6] >= 1&&cnt[3] >= 1&&cnt[2] >= 1)
        return true;
    if(cnt[6] >= 1&&cnt[4]>=1 && cnt[0] >= 1 )
        return true;
    if(cnt[6] >= 1&&cnt[4]>=1 && cnt[8] >= 1)
        return true;
    if(cnt[6] >= 1 && cnt[5]>=1&&cnt[6]>=1)
        return true;
    if(cnt[6] >= 2&& cnt[4] >= 1 )
        return true;
    if(cnt[6] >= 1 && cnt[7] >= 2 && cnt[2] >= 1)
        return true;    
    if(cnt[6] >= 1 && cnt[8] >= 1 && cnt[0] >= 1)
        return true;                  
    if(cnt[6] >= 1 && cnt[8] >= 2)
        return true;
    if(cnt[6] >= 2 && cnt[9] >= 1)
        return true;           

    if(cnt[7] >=1 && cnt[0] >= 1 && cnt[4] >= 1)
        return 1;
    if(cnt[7] >= 1 && cnt[1] >= 1 && cnt[2] >= 1)
        return 1;
    if(cnt[7] >= 1 && cnt[2] >= 1&& cnt[0] >= 1)
        return 1;
    if(cnt[7] >= 1&&cnt[2] >= 1&&cnt[8] >= 1)
        return 1;
    if(cnt[7] >= 1&&cnt[3]>=1&&cnt[6] >= 1)
        return true;
    if(cnt[7] >= 1 && cnt[4] >= 2 )
        return true;
    if(cnt[7] >= 1&&cnt[5]>=1 &&cnt[2] >= 1)
        return true;
    if(cnt[7] >= 1 && cnt[6]>=1&&cnt[0]>=1)
        return true;
    if(cnt[7] >= 1&& cnt[6] >= 1 && cnt[8] >= 1)
        return true;
    if( cnt[7] >= 2 && cnt[6] >= 1)
        return true;    
    if(cnt[7] >= 1 && cnt[8] >= 1 && cnt[4] >= 1)
        return true;
    if(cnt[7] >= 1 && cnt[9] >= 1 && cnt[2] >= 1)
        return true;       

    if(cnt[0] >=2 && cnt[8] >= 1)
        return 1;
    if( cnt[0] >= 1 && cnt[8] >= 2)
        return 1;
    if(cnt[8]>=1&&cnt[6] >= 1 && cnt[1] >= 1)
        return 1;
    if(cnt[8] >= 1&&cnt[2] >= 1&&cnt[4]>=1)
        return 1;
    if(cnt[8] >= 1&&cnt[3] >= 1&&cnt[2] >= 1)
        return true;
    if(cnt[8] >= 1&&cnt[4]>=1 && cnt[0] >= 1 )
        return true;
    if(cnt[4]>=1 && cnt[8] >= 2)
        return true;
    if(cnt[8] >= 1 && cnt[5]>=1&&cnt[6]>=1)
        return true;
    if(cnt[8]>=1&&cnt[6] >= 1&& cnt[4] >= 1 )
        return true;
    if(cnt[8] >= 1 && cnt[7] >= 2 && cnt[2] >= 1)
        return true;    
    if(cnt[8] >= 2 && cnt[0] >= 1)
        return true;                  
    if(cnt[8] >= 3)
        return true;
    if(cnt[8]>=1 &&cnt[6] >= 1 && cnt[9] >= 1)
        return true;        

    if(cnt[9] >=1 && cnt[0] >= 1 && cnt[4] >= 1)
        return 1;
    if(cnt[9] >= 1 && cnt[1] >= 1 && cnt[2] >= 1)
        return 1;
    if(cnt[9] >= 1 && cnt[2] >= 1&& cnt[0] >= 1)
        return 1;
    if(cnt[9] >= 1&&cnt[2] >= 1&&cnt[8] >= 1)
        return 1;
    if(cnt[9] >= 1&&cnt[3]>=1&&cnt[6] >= 1)
        return true;
    if(cnt[9] >= 1 && cnt[4] >= 2 )
        return true;
    if(cnt[9] >= 1&&cnt[5]>=1 &&cnt[2] >= 1)
        return true;
    if(cnt[9] >= 1 && cnt[6]>=1&&cnt[0]>=1)
        return true;
    if(cnt[9] >= 1&& cnt[6] >= 1 && cnt[8] >= 1)
        return true;
    if( cnt[9] >= 1&&cnt[7]>=1 && cnt[6] >= 1)
        return true;    
    if(cnt[9] >= 1 && cnt[8] >= 1 && cnt[4] >= 1)
        return true;
    if(cnt[9] >= 2 && cnt[2] >= 1)
        return true;

    return false;                      
}

int main(){
    
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> s;
    memset(cnt, 0, sizeof cnt);
    for(int i = 0; i < s.length(); i++){
    
    
        cnt[s[i]-'0']++;
    }
    if(judge()){
    
    
        cout << "Yes" << "\n";
    }
    else{
    
    
        cout << "No" << "\n";
    }
    return 0;
}

E - Transformable Teacher

在这里插入图片描述
题意：
有一长度为奇数n的数组a,和长度为m的数组b,现要求从b中选择一个数放到a中,并将a分成(n+1)/2个数对,求最小的所有数对差的和。
思路：
对n数组排序，二分查找每一个m在原数组的所在位置，之前预处理一下原数组的前后缀，就可以了。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

int n, m;
ll h[200010];
ll w[200010];
ll pre[200010];
ll suf[200010];

int main(){
    
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n >> m;
    for(int i = 1; i <= n; i++){
    
    
        cin >> h[i];
    }
    sort(h+1, h+1+n);
    for(int i = 1; i <= m; i++){
    
    
        cin >> w[i];
    }
    for(int i = 2; i <= n; i+=2){
    
    
        pre[i] = pre[i-2] + abs(h[i]-h[i-1]);
    }
    for(int i = n-1; i >= 1; i-=2){
    
    
        suf[i] = suf[i+2] + abs(h[i] -h[i+1]); 
    }

    ll ans = 1e18;
    for(int i = 1; i <= m; i++){
    
    
        int t = lower_bound(h+1, h+1+n, w[i]) - h;
        if(t%2 == 0){
    
    
            t--;
        }
        ans = min(ans, pre[t-1] + suf[t+1] + abs(w[i] - h[t]));
    }
    cout << ans << "\n";
    return 0;
}

F - Silver Woods

在这里插入图片描述
题意：
空间区域的上下界是-100和100。有n个点，不重合。问是否可以找到一个r，让以r为半径的圆，可以从 ( − 1 e 9 , 0 ) (-1e9, 0) (−1e9,0)移动到 ( 1 e 9 , 0 ) (1e9, 0) (1e9,0)，且不经过n个点和边界，求r的最大值。
思路：
r的大小显然可以二分得到。对于每一个r，如果存在两个点间的距离小于2r，就不能从这两个点间走；如果一个点和边界距离小于2r，就不能从这个点和次边界中经过。于是我们考虑带虚点的并查集，n个点是1到n，上边界是n+1，下边界是0。如果一个点到边界的距离小于2r，就把点和这个边界连到一个连通分量里面。如果两个点距离小于2r，就把这两个点连到一个连通分量里面。如果上下边界最后连到一个连通分量就表示这个r不能被满足，否则就可以。

#include<bits/stdc++.h>
using namespace std;

int n;
int x[105], y[105];
int f[105];

void init(int n){
    
    
    for(int i = 0; i <= n; i++){
    
    
        f[i] = i;
    }
}

int find(int x){
    
    
    return (f[x] == x?x:f[x] = find(f[x]));
}

void Union(int x, int y){
    
    
    int fx = find(x), fy = find(y);
    if(x != y){
    
    
        f[fx] = fy;
    }
}

bool check(double k){
    
    
    init(n+1);
    for(int i = 1; i <= n; i++){
    
    
        //和顶上连接
        if(100.0 - (double)y[i] < 2*k){
    
    
            Union(i, n+1);
        }
    }
    for(int i = 1; i <= n; i++){
    
    
        if((double)y[i] + 100.0 < 2*k){
    
    
            Union(i, 0);
        }
    }

    for(int i = 1; i <= n; i++){
    
    
        for(int j = i+1; j <= n; j++){
    
    
            if((1.0*x[i] - 1.0*x[j])*(1.0*x[i] - 1.0*x[j]) + (1.0*y[i] - 1.0*y[j])*(1.0*y[i] - 1.0*y[j]) < 4.0*k*k){
    
    
                Union(i, j);
            }
        }
    }
    if(find(0) == find(n+1)){
    
    
        return false;
    }
    return true;
}


int main(){
    
    
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    for(int i = 1; i <= n; i++){
    
    
        cin >> x[i] >> y[i];
    }

    double l = 0.0, r = 100.0;  
    while(r - l > 1e-8){
    
    
        double mid = (l+r)/2;
        if(check(mid)){
    
    
            l = mid;
        }
        else{
    
    
            r = mid;
        }

    }
    cout << r << "\n";
}

猜你喜欢

转载自blog.csdn.net/Einsteinme/article/details/112353665
今日推荐
周排行
Android图片与下拉框
java常用的设计模式之单例模式
zabbix自动化监控之自动注册
杨老师课堂之Excel VBA 程序开发第八讲使用工作表函数
Android 去掉底部虚拟导航栏
Android Studio 3.2 Beta 4 发布，功能改进和修复
Linux-3.5_总线驱动设备
Qt QTableView QStandardItemModel用法
session处理
分享几个实用的方法
每日归档
更多
2025-02-06(0)
2025-02-05(0)
2025-02-04(0)
2025-02-03(0)
2025-02-02(0)
2025-02-01(0)
2025-01-31(0)
2025-01-30(0)
2025-01-29(0)
2025-01-28(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022