目录
做题的HINT
做题的时候不要眼高手低,首先把思路想好,然后再写代码可以事半功倍(指的是,费力小,但是功效大,经常指在做事的时候,使用了正确的方法,付出比别人少,但是收获却比别人多,语文都有点遗忘了哈哈哈哈),
还有上了一学期卜老师的算法,最重要的记住是从最简单的case入手,卜老师的课确实让我受益匪浅,不过想要提高自己的水平还是有很长的路要走,多刷题多思考,不要怕难。你是在进步的~
简单的问题也许不简单,你以为简单,实际上做起来并不,一定不要眼高手低!
最长回文子序列
子序列:不连续
子数组/子串:连续
题目链接:https://leetcode-cn.com/problems/longest-palindromic-subsequence/
难度中等
给定一个字符串 s ,找到其中最长的回文子序列,并返回该序列的长度。可以假设 s 的最大长度为 1000 。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 "bb"。
提示:
1 <= s.length <= 1000s只包含小写英文字母
思路
dp[i][j] 表示 s[i...j]的最长回文子序列
base case i=j --> 子序列只有一个字符 dp[i][j]=1
i>j ->不存在 dp[i][j]=0
dp[i][j]
if s[i]==s[j] dp[i][j]=dp[i+1][j-1]+1
else
dp[i][j]=max(dp[i+1][j],dp[i][j-1])
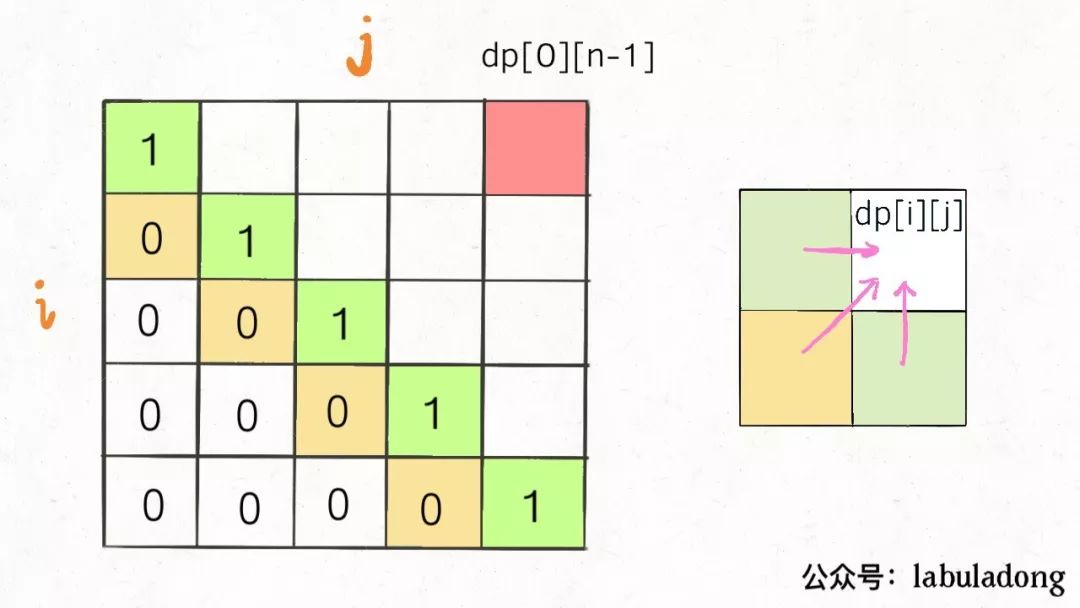
观察递推关系得到解的结构:
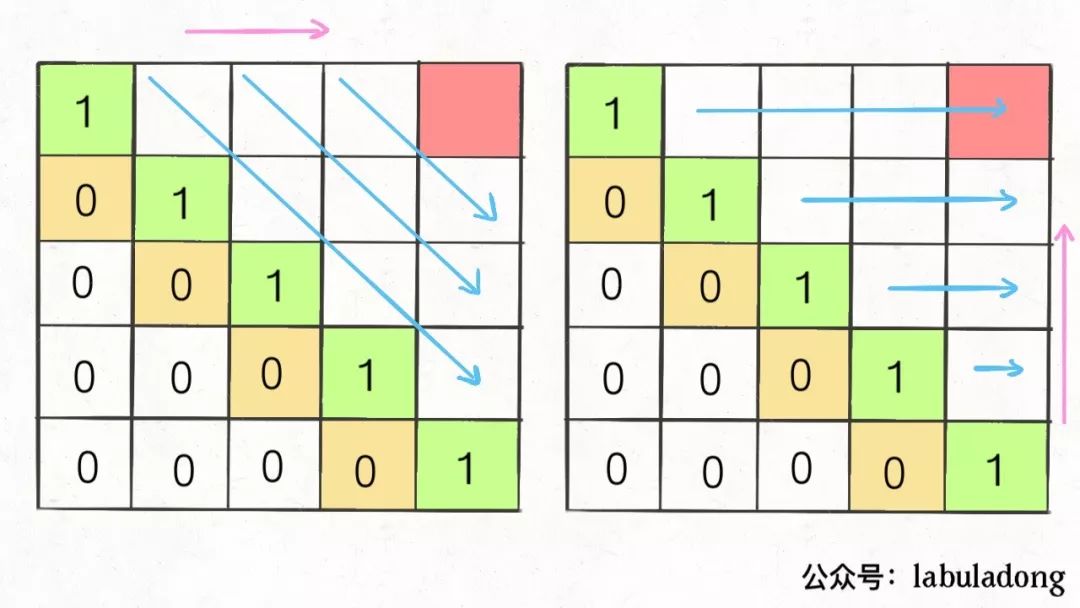
代码
int longestPalindromeSubseq(string s) {
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n,0));
for(int i=0;i<n;i++) dp[i][i]=1;
for(int i=n-2;i>=0;i--){
for(int j=i+1;j<n;j++){
if(s[i]==s[j]){
dp[i][j]=dp[i+1][j-1]+2;
}
else{
dp[i][j]=max(dp[i][j-1],dp[i+1][j]);
}
}
}
return dp[0][n-1];
}1312. 让字符串成为回文串的最少插入次数
难度困难
给你一个字符串 s ,每一次操作你都可以在字符串的任意位置插入任意字符。
请你返回让 s 成为回文串的 最少操作次数 。
「回文串」是正读和反读都相同的字符串。
示例 1:
输入:s = "zzazz"
输出:0
解释:字符串 "zzazz" 已经是回文串了,所以不需要做任何插入操作。
示例 2:
输入:s = "mbadm"
输出:2
解释:字符串可变为 "mbdadbm" 或者 "mdbabdm" 。
示例 3:
输入:s = "leetcode"
输出:5
解释:插入 5 个字符后字符串变为 "leetcodocteel" 。
示例 4:
输入:s = "g"
输出:0
示例 5:
输入:s = "no"
输出:1
提示:
1 <= s.length <= 500s中所有字符都是小写字母。
思路
dp[i][j] 类似上一题的定义
dp[i][j] 表示 s[i...j] 能让这段字符串变成回文串需要插入的最小次数
base case dp[i][i]=0
if s[i]==s[j] dp[i][j]=dp[i+1][j-1]
else dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1
代码
int minInsertions(string s) {
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n,0));
for(int i=n-2;i>=0;i--){
for(int j=i+1;j<n;j++){
if(s[i]==s[j]){
dp[i][j]=dp[i+1][j-1];
}
else{
dp[i][j]=min(dp[i][j-1],dp[i+1][j])+1;
}
}
}
return dp[0][n-1];
}
注:文章中图片非原创,来源见水印