


// 基本的 DFS 框架:每次搜索四个相邻方格
void dfs(int[][] grid, int r, int c) {
dfs(grid, r - 1, c); // 上边相邻
dfs(grid, r + 1, c); // 下边相邻
dfs(grid, r, c - 1); // 左边相邻
dfs(grid, r, c + 1); // 右边相邻
}

// 处理方格位于网格边缘的情况
void dfs(int[][] grid, int r, int c) {
// 若坐标不合法,直接返回
if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
return;
}
// 若该方格不是岛屿,直接返回
if (grid[r][c] != 1) {
return;
}
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}

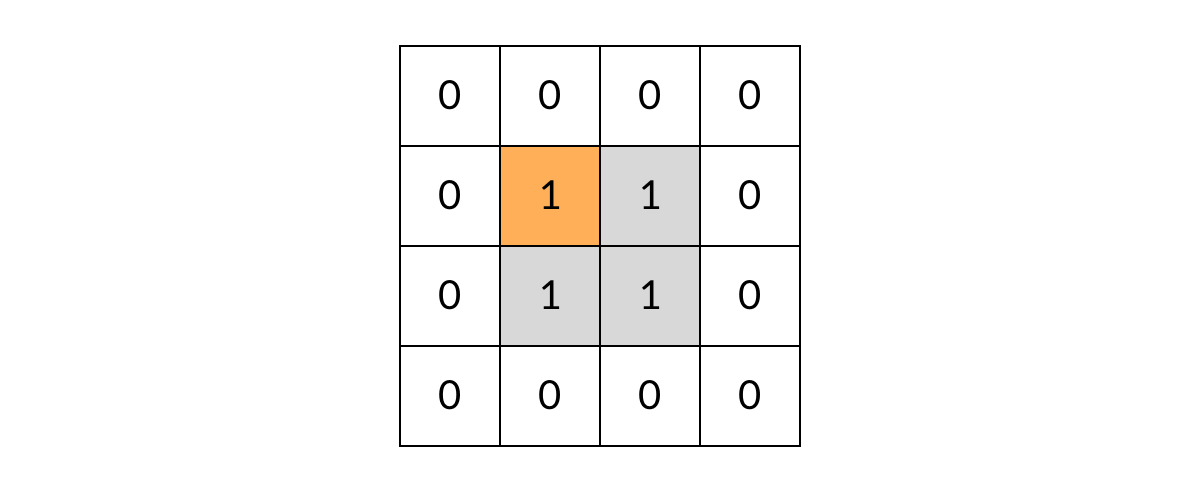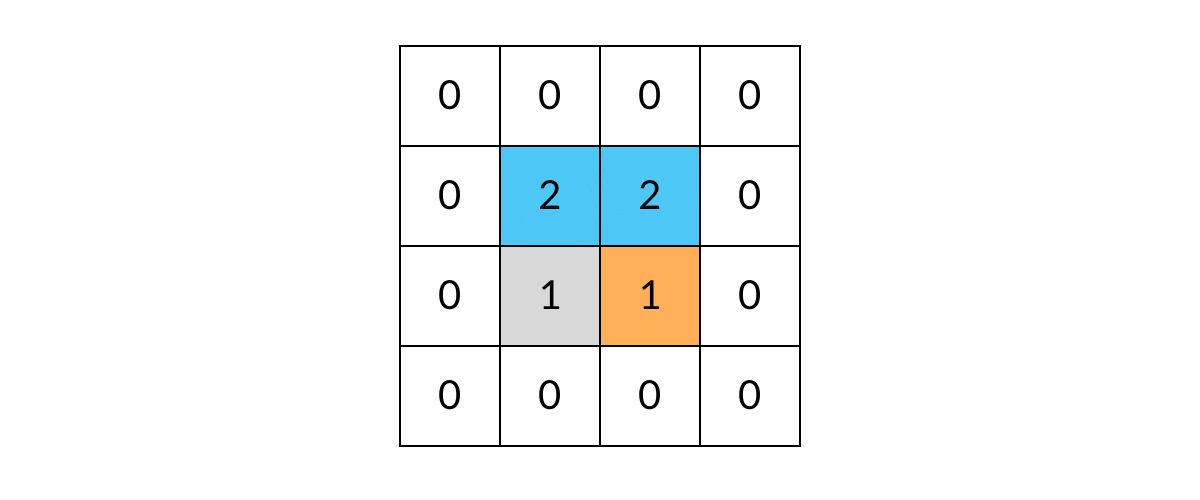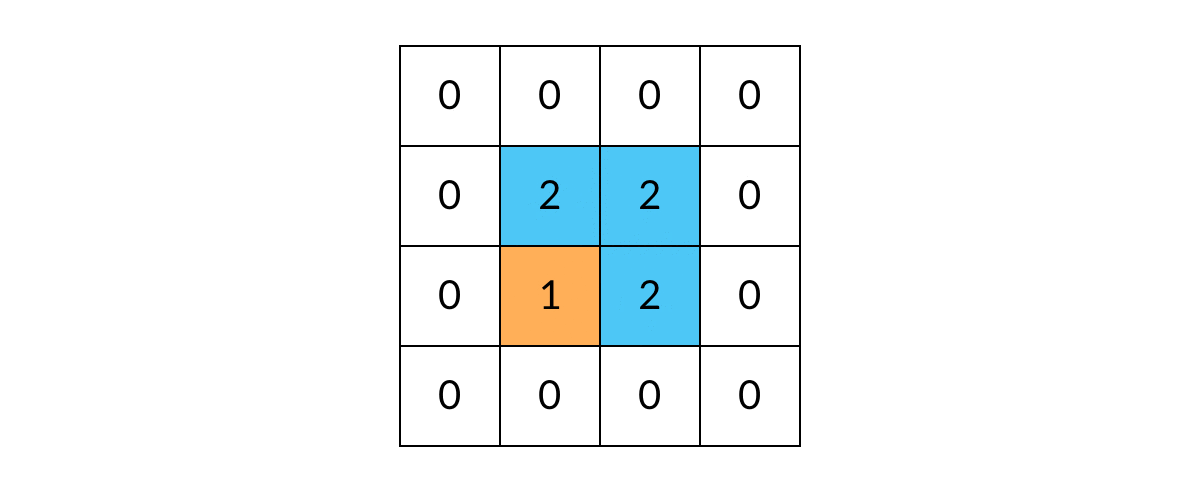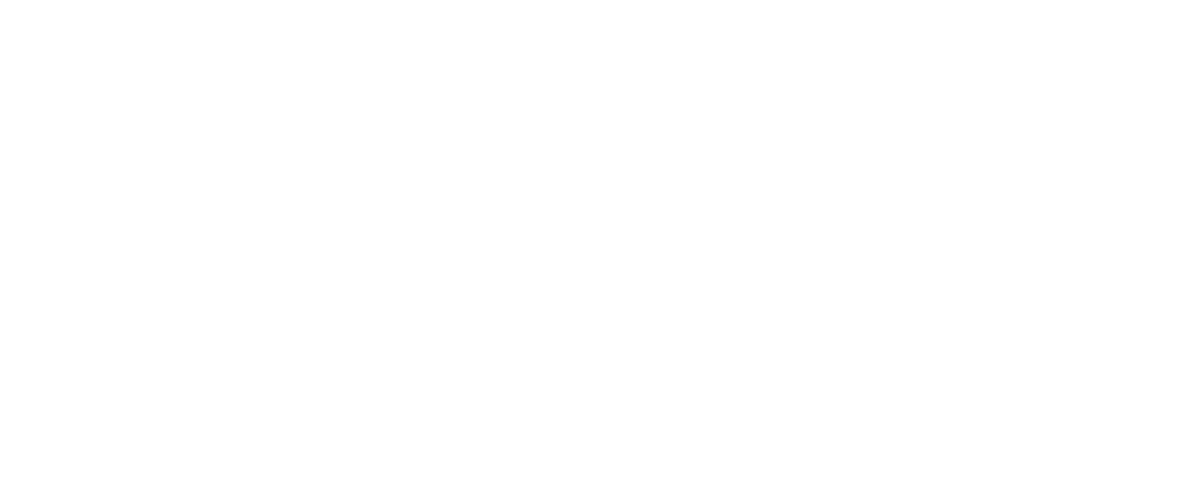

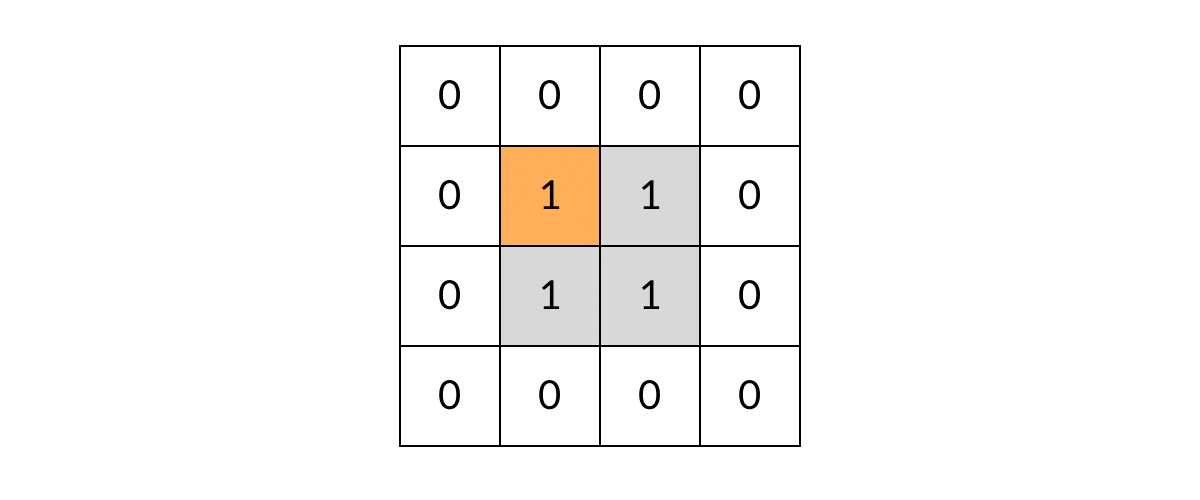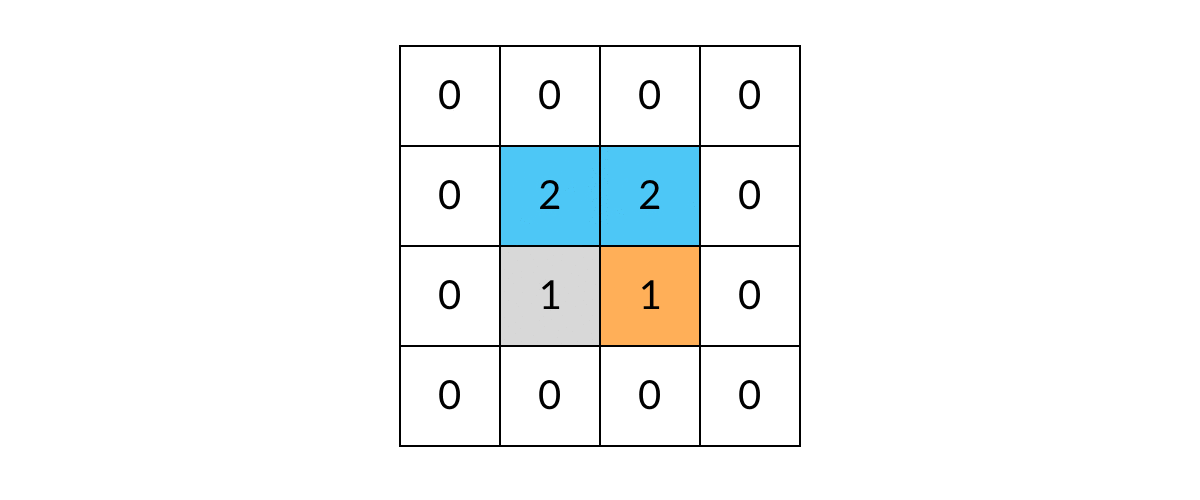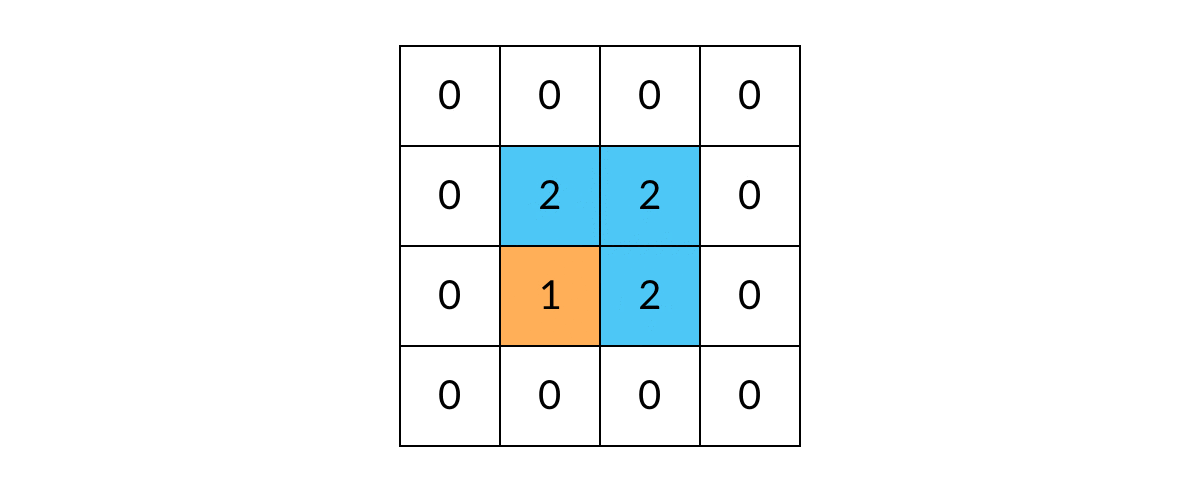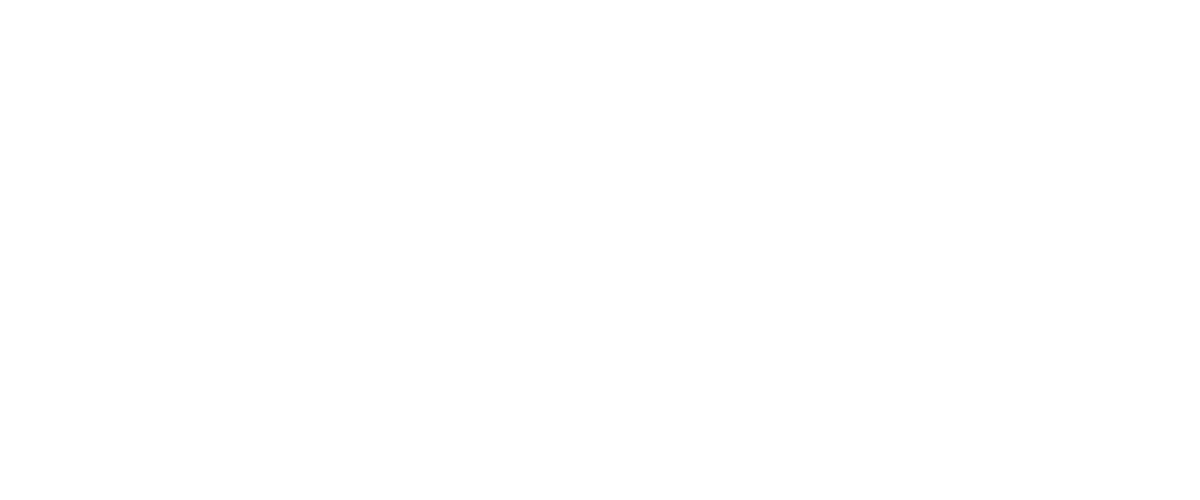

// 标记已遍历过的岛屿,不做重复遍历
void dfs(int[][] grid, int r, int c) {
if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
return;
}
// 已遍历过(值为2)的岛屿在这里会直接返回,不会重复遍历
if (grid[r][c] != 1) {
return;
}
grid[r][c] = 2; // 将方格标记为"已遍历"
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}



int dfs(int[][] grid, int r, int c) {
// 从一个岛屿方格走向网格边界,周长加 1
if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
return 1;
}
// 从一个岛屿方格走向水域方格,周长加 1
if (grid[r][c] == 0) {
return 1;
}
if (grid[r][c] != 1) {
return 0;
}
grid[r][c] = 2;
return dfs(grid, r - 1, c)
+ dfs(grid, r + 1, c)
+ dfs(grid, r, c - 1)
+ dfs(grid, r, c + 1);
}

public int islandPerimeter(int[][] grid) {
for (int r = 0; r < grid.length; r++) {
for (int c = 0; c < grid[0].length; c++) {
if (grid[r][c] == 1) {
// 题目限制只有一个岛屿,计算一个即可
return dfs(grid, r, c);
}
}
}
return 0;
}
int dfs(int[][] grid, int r, int c) {
if (!(0 <= r && r < grid.length && 0 <= c && c < grid[0].length)) {
return 1;
}
if (grid[r][c] == 0) {
return 1;
}
if (grid[r][c] != 1) {
return 0;
}
grid[r][c] = 2;
return dfs(grid, r - 1, c)
+ dfs(grid, r + 1, c)
+ dfs(grid, r, c - 1)
+ dfs(grid, r, c + 1);
}
测试DFS
public class Test3 {
public static void main(String[] args) {
int[][] arr = {
{
0, 1, 0, 0},
{
0, 1, 0, 0},
{
0, 1, 1, 0},
{
0, 1, 0, 1},
};
dfs(arr, 0, 1);
}
public static void dfs(int[][] arr, int r, int c) {
//越界后到上一次位置
if(!(0 <= r && r < arr.length && 0 <= c && c < arr[0].length)) {
return;
}
//该位置不能走 回到上一层位置
if(arr[r][c] != 1) {
return;
}
//可以走 将该位置标记已走
arr[r][c] = 2;
System.out.println("走的位置为:{"+r+","+c+"}");
dfs(arr, r + 1, c);
dfs(arr, r - 1, c);
dfs(arr, r, c + 1);
dfs(arr, r, c - 1);
}
}
可以看出并不是所有的元素都可以走到,有一个元素处于对角线位置 周围又都是0 为了保证每个元素都要走到所以要两层for循环来保证

public class Test3 {
public static void main(String[] args) {
int[][] arr = {
{
0, 1, 0, 0},
{
0, 1, 0, 0},
{
0, 1, 1, 0},
{
0, 1, 0, 0},
};
for(int i = 0; i < arr.length; i++) {
for(int j = 0; j < arr[0].length; j++) {
if(arr[i][j] == 1) {
System.out.println(dfs(arr, i, j));
}
}
}
}
public static int dfs(int[][] arr, int r, int c) {
//越界后到上一次位置
if(!(0 <= r && r < arr.length && 0 <= c && c < arr[0].length)) {
return 1;
}
//该位置不能走 回到上一层位置
if(arr[r][c] == 0) {
return 1;
}
if(arr[r][c] == 2) {
return 0;
}
//可以走 将该位置标记已走
arr[r][c] = 2;
System.out.println("走的位置为:{"+r+","+c+"}");
return
dfs(arr, r + 1, c)+
dfs(arr, r - 1, c)+
dfs(arr, r, c + 1)+
dfs(arr, r, c - 1);
}
}
