一、简介
1 模拟退火算法的应用背景
模拟退火算法提出于1982年。Kirkpatrick等人首先意识到固体退火过程与优化问题之间存在着类似性;Metropolis等人对固体在恒定温度下达到热平衡过程的模拟也给他们以启迪。通过把Metropolis 算法引入到优化过程中,最终得到一种对 Metropolis 算法进行迭代的优化算法,这种算法类似固体退火过程,称之为“模拟退火算法”。
模拟退火算法是一种适合求解大规模组合优化问题的随机搜索算法。目前,模拟退火算法在求解 TSP,VLSI 电路设计等组合优化问题上取得了令人满意的结果。将模拟退火算法同其它的计算智能方法相结合,应用到各类复杂系统的建模和优化问题中也得到了越来越多的重视,已经逐渐成为一种重要的发展方向。
2 模拟退火算法介绍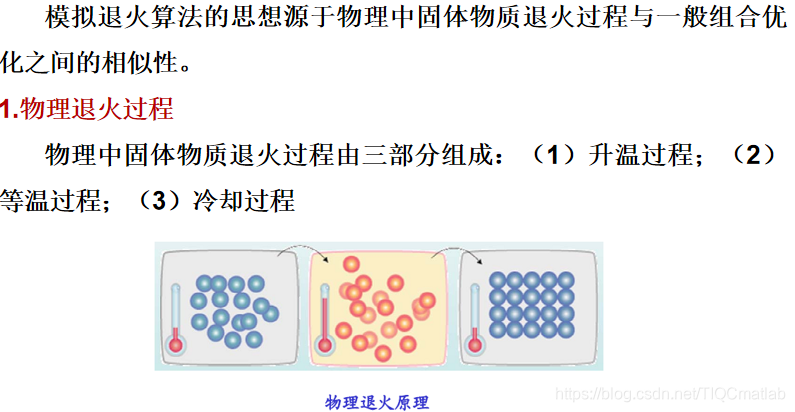


3 模拟退火算法的参数
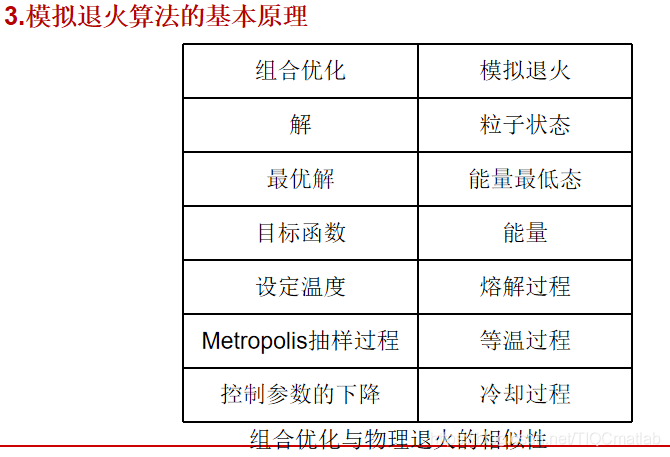
模拟退火是一种优化算法,它本身是不能独立存在的,需要有一个应用场合,其中温度就是模拟退火需要优化的参数,如果它应用到了聚类分析中,那么就是说聚类分析中有某个或者某几个参数需要优化,而这个参数,或者参数集就是温度所代表的。它可以是某项指标,某项关联度,某个距离等等。
二、源代码
% clc;
close all;clear all;
p=[ 1739.94 1675.15 2395.96
373.3 3087.05 2429.47
1756.77 1652 1514.98
864.45 1647.31 2665.9
222.85 3059.54 2002.33
877.88 2031.66 3071.18
1803.58 1583.12 2163.05
2352.12 2557.04 1411.53
401.3 3259.94 2150.98
363.34 3477.95 2462.86
1571.17 1731.04 1735.33
104.8 3389.83 2421.83
499.85 3305.75 2196.22
2297.28 3340.14 535.62
2092.62 3177.21 584.32
1418.79 1775.89 2772.9
1845.59 1918.81 2226.49
2205.36 3243.74 1202.69
2949.16 3244.44 662.42
1692.62 1867.5 2108.97
1680.67 1575.78 1725.1
2802.88 3017.11 1984.98
172.78 3084.49 2328.65
2063.54 3199.76 1257.21
1449.58 1641.58 3405.12
1651.52 1713.28 1570.38
341.59 3076.62 2438.63
291.02 3095.68 2088.95
237.63 3077.78 2251.96
1702.8 1639.79 2068.74
1877.93 1860.96 1975.3
867.81 2334.68 2535.1
1831.49 1713.11 1604.68
460.69 3274.77 2172.99
2374.98 3346.98 975.31
2271.89 3482.97 946.7
1783.64 1597.99 2261.31
198.83 3250.45 2445.08
1494.63 2072.59 2550.51
1597.03 1921.52 2126.76
1598.93 1921.08 1623.33
1243.13 1814.07 3441.07
2336.31 2640.26 1599.63
354 3300.12 2373.61
2144.47 2501.62 591.51
426.31 3105.29 2057.8
1507.13 1556.89 1954.51
343.07 3271.72 2036.94
2201.94 3196.22 935.53
2232.43 3077.87 1298.87
1580.1 1752.07 2463.04
1962.4 1594.97 1835.95
1495.18 1957.44 3498.02
1125.17 1594.39 2937.73
24.22 3447.31 2145.01
1269.07 1910.72 2701.97
1802.07 1725.81 1966.35
1817.36 1927.4 2328.79
1860.45 1782.88 1875.13
];
[num,n]=size(p); %样品数目
centernum=4; %类别数目
IDXO=[1 2 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 ];
% size(IDXO)
CO(1,:)=[ 1739.94 1675.15 2395.96];
CO(2,:)=[373.3 3087.05 2429.47];
CO(3,:)=[1756.77 1652 1514.98];
% s1=find(IDXO==1);%聚类号为1的样品在p中的序号
% s11=p(s1,:)
s4=find(IDXO==4);%聚类号为4的样品在p中的序号
s44=p(s4,:);%全部为4类的样品矩阵
CO(4,:)=[sum(s44(:,1))/59,sum(s44(:,2))/59,sum(s44(:,3))/59];%第4类的中心
JO=0;
j1=0; j2=0; j3=0; j4=0;
for i=1:num
if IDXO(i)==4
j4=j4+sqrt((p(i,1)-CO(1,1))^2+(p(i,2)-CO(1,2))^2+(p(i,3)-CO(1,3))^2);
end
end
三、运行结果

完整代码或者代写添加QQ1575304183