统计学理论—抽样分布

在学习统计学贾书的过程，在第6—14章节出有许多需要理解与记忆的公式和概念，在此通过博客的形式做一次梳理，主要内容为统计学中抽样分布、假设检验、参数估计、分类数据分析、方差分析、一元二元线性分析、时间序列分析、指数的理论知识，不足之处望多多指正。

${\chi }^2$分布

• 定义
  但总体$X\sim N\left(\mu ,{\sigma }^2\right)$ 从中抽取容量为n的样本，则有$\frac{{\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2}{{\sigma }^2}\sim {\chi }^2(n-1)$
• 分布概率分布图像：
  
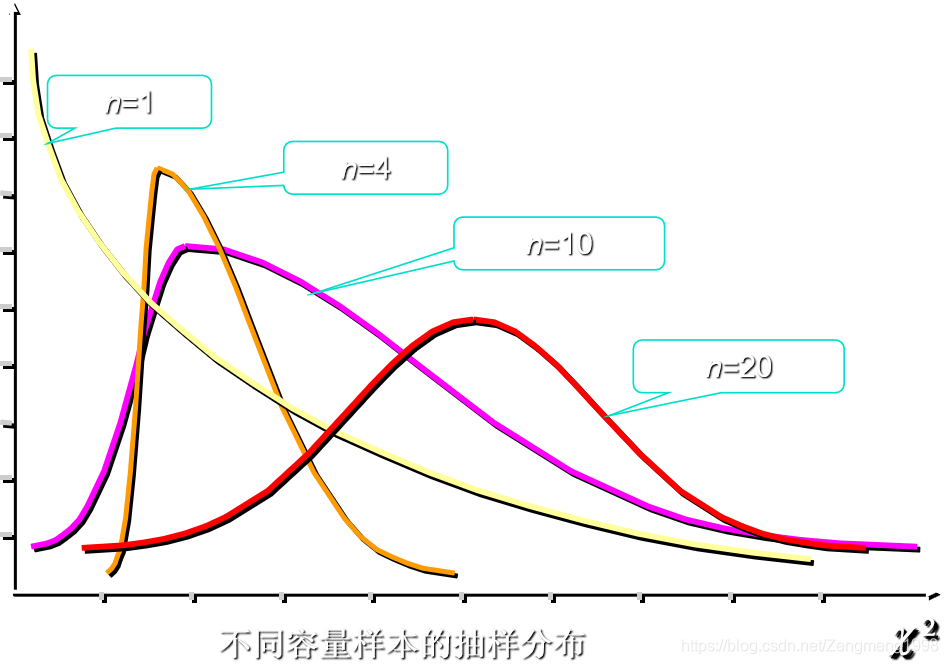
• 常用性质
  （1）期望：n
  （2）方差： 2n
  （3） 分布的形状取决于其自由度n的大小，通常为不对称的正偏分布，但随着自由度的增大逐渐趋于对称
  （4）具有可加性

t分布

• 定义
  设随机变量$X\sim N(0，1)$，$Y\sim {\chi }^2(n)$,则$t=\frac{X}{\sqrt{Y/n}}$其分布称为t分布，其自由度为n记做t（n）。
• 分布图像（与正态分布对比）
  

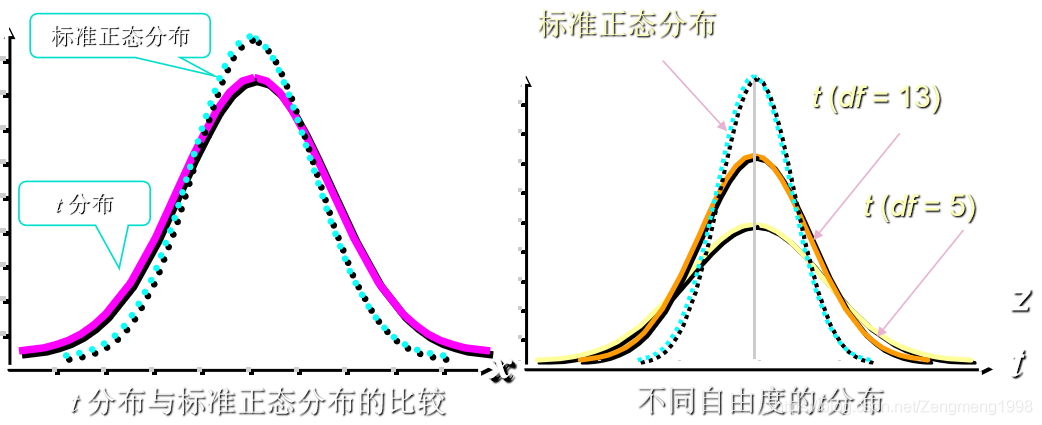
F分布

• 定义
  设若U为服从自由度为$n_1$的${\chi }^2$分布;V为服从自由度为$n_2$的${\chi }^2$分布即：$V\sim {\chi }^2(n_1)$;$U\sim {\chi }^2(n_1)$,则称F为服从自由度$n_1$和$n_2$的F分布，记为：$F\sim F(n_1，n_2)$

• 图像（不同自由度的F分布）

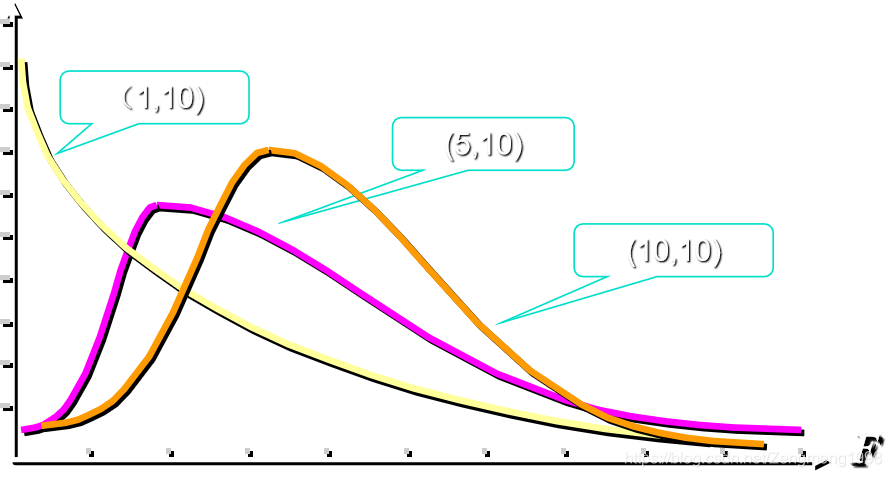
中心极限定理

• 定义
  从均值为$\mu$，方差为${\sigma }^2$的一个任意总体中抽取容量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为μ、方差为σ2/n的正态分布
  (简言之：当样本容量足够大时(n >=30) ，样本均值的抽样分布逐渐趋于正态分布)
• 形象化理解：
  

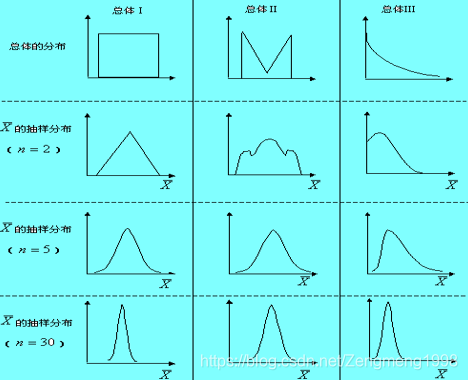
参考

《统计学》 第7版_贾俊平