Misc没别的意思给你签个到顺便给你看看我老婆
Lsb隐写
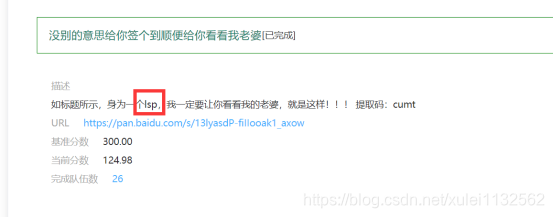
由题目的lsp想到lsb隐写,使用
打开,三个低位为0,
然后去掉之间的空格,就对了。
大鸟转转转转转转转转转
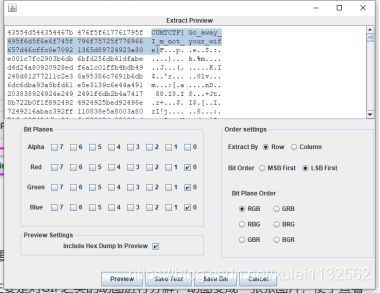
同样是使用相同的软件,

一帧一帧的分析
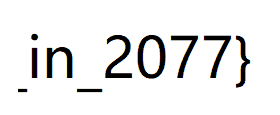

拼接起来就出来了
简单的rsa
from Crypto.Util.number import *
import gmpy2
k = 33168381182273613039378043939021834598473369704339979031406271655410089954946280020962013567831560156371101600701016104005421325248601464958972907319520487
c = 15648371218931722790904370162434678887479860668661143723578014419431384242698608484519131092011871609478799077215927112238954528656254346684710581567304227780228595294264728729958171950314042749100472064919234676544341981418897908716041285489451559413615567610248062182987859379618660273180094632711606707044369369521705956617241028487496003699514741969755999188620908457673804851050978409605236834130689819372028797174206307452231481436775711682625666741103384019125790777595493607264935529404041668987520925766499991295444934206081920983461246565313127213548970084044528257990347653612337100743309603015391586841499
e = 4097
phi = k-1
d=gmpy2.invert(e,phi)
flag = pow(c,d,k)
print(long_to_bytes(flag))
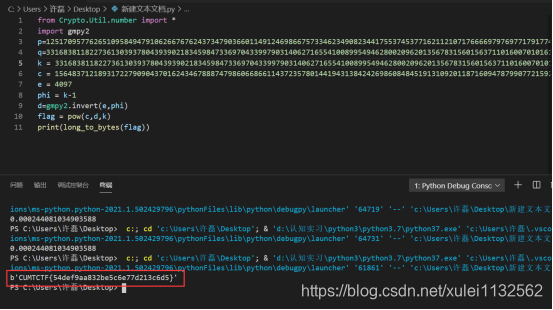
Rsa算法e公钥已知,c(密文)已知,给了一个元组,第一个元素是公钥,第二个是私钥k即是n,所以求出d来,pow(c,d,k)即可求出明文。
参考网站https://blog.cryptohack.org/cryptoctf2020
网上的思路:
The challenge encrypts the flag with a modulus
N=(p∗q∗r)∗(p+q+r)
and gives the output n=pqr, k=p+q+r. To totally break the cryptosystem, we would want to find the totient of the modulus

ϕ(N)=(p−1)(q−1)(r−1)(p+q+r−1)
but we can simplify this when the encrypted message m is small enough. If we have m<k, we can instead find ϕ(k)=k−1, and find e−1modϕ(k), and solve!
Observe that for any n,l, as long as l|n, any equivalence a≡b(modn) also holds mod l: a≡b(modl) (but note that the other way around does not necessarily hold). To fully see this, we can write
a⇔a⇒a≡b(modn)=b+kn=b+ktl(since l|n, so n=tl)≡b(modl)
So, since k|n, we can solve m≡m1+ϕ(k)(modk) as if it was a single-prime RSA problem. And because m<k, the residue [m]k (the rest when dividing m by k) is exactly equal to m.
乱写的密码
分析逻辑,可以看出是,替换密码,一个字母对应另一个字母,且,只出现一次
本来想用脚本,通过字频分析出来,但是,做了好久没做出来,便试着在网上搜索在线破解的网站,结果发现果然走了弯路
破解网站的连接https://quipqiup.com/

ez_rsa
这题出题后,立马用谷歌搜,果然搜到了原题,果然拿了一血
from Crypto.Util.number import *
from gmpy2 import invert
n=17986052241518124152579698727005505088573670763293762110375836247355612011054569717338676781772224186355540833136105641118789391002684013237464006860953174190278718294774874590936823847040556879723368745745863499521381501281961534965719063185861101706333863256855553691578381034302217163536137697146370869852180388385732050177505306982196493799420954022912860262710497234529008765582379823928557307038782793649826879316617865012433973899266322533955187594070215597700782682186705964842947435512183808651329554499897644733096933800570431036589775974437965028894251544530715336418443795864241340792616415926241778326529055663
e=65537
enc=17505679398266502116464734134128725340247050682772207798718112582701162398326982870035320307354098156145675458669731605067821790146061040637109327455205893324813052120216078570610930872674755246099365674625431655007219684642963335426955196473587347290657014023186920750946928312239116919090008342804123453311441848155223191179999664929660663345568499980778425899869956228245802722031728956228667784902213280684273577858909961747898300981963006329584725303446719192681170020458749808054637224882633325702468591074293728614333360418157985394943356536309321590140334348949095024011542798810065149061943391776967748248277703228
beta=11864389277042761216996641604675717452843530574016671576684180662096506094587545173005905433938758559675517932481818900399893444422743930613073261450555599
tip = (n-1)//(2*beta)
xy1=tip//beta
def attack(xy1):
while True:
try:
xy1=xy1-2
d=invert(e,2*xy1*pow(beta,2))
c=pow(3,e,n)
if pow(c,d,n)==3:
return d
else:
continue
except:
continue
d=attack(xy1)
print long_to_bytes(pow(enc,d,n))
那么对于获得 x + y这个问题,由于beta是512位,n的位数为 2068,那么平均一下p的位数就是1034了,那么x的位数大概就是1034 – 1 – 512 = 521,x + y 与beta位数差了10位左右,完全是可以暴力的范围,n = p * q = 4xybeta ^ 2 + 2(x+y )beta + 1
很自然的能得到 tip = (n-1)//beta
然后我们给tip模上beta,我们就能得到 (x+y)%beta ,如果我们能够获得x + y,那么显然我们也能获得x * y,然后解个方程即可获得x和y,然后就能获得p和q,继而解密rsa得到flag,基本上就是用py2运行,简单修改了对应的参数,要使用
Try
Except语句,因为存在爆破不成功,但需要继续continue
(显示无法求逆元)
一开始的报错,估计是因为没有使用报错语句来写
由于本人的py2环境忘记打到哪里去了,所以我写的脚本,队友运行的exp
出来签到啦
参考网站https://www.cnblogs.com/crybaby/p/12940219.html
参考脚本
写出exp
from Crypto.Cipher import AES
def xor(p1, p2):
tmp = ''
for i in range(len(p2)):
tmp += chr(ord(p1[i]) ^ ord(p2[i]))
return tmp
key = "\t\xe6\x85]):\x1b\x86\xffD\xf1\x89H\xb1\x9b\xac"
cipherText1 = "ed64978b91ef5b62561a44c8f529b91f".decode("hex")
cipherText = "fd6dd5e0f9ab258b2bc9c813177e3ad677116d2f08c69517d0e7796c1f5e06ba95c3de5a139bb687bf3e779a0730e47c".decode("hex")
plainText = "CBC_Cr4cked_succ"
fakeIV = "aaaaaaaaaaaaaaaa"
fakeIVAes = AES.new(key, AES.MODE_CBC, fakeIV)
fakePlainText = fakeIVAes.decrypt(cipherText1)
enc_msg = xor(fakePlainText, fakeIV)
iv = xor(enc_msg, plainText)
print len(iv)
print "iv is : " + iv
aes = AES.new(key, AES.MODE_CBC, iv)
flag = aes.decrypt(cipherText)
print flag
这个密码算法,模式就是密码学课上学到的模式,相信密码学过了的都会,由于本人没有py2环境,所以还是队友运行的
做出了第一关,然后第二关
flag = "bxsyyds{
xxxxxxx}
assert flag.startswith("bxsyyds{")
assert flag.endswith("}")
assert len(flag)==16
def lfsr(R,mask):
output = (R << 1) & 0xfffffff
i=(R&mask)&0xfffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[8:-1],16)
mask=0b1001000000100000001000100101
f=open("result","w")
for i in range(100):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()
做过密码学实验,便很容易发现是lsfr流密码,需要找到result对应的二进制模式的前7*4=28个二进制流
由于一开始粗心,把16进制转化成2进制转化错了!!!
挺多弯路
然后经过短暂的思考人生,检查一下二进制对不对,果然转化错了
re1
参考
https://driverxdw.github.io/2019/04/24/2019%E8%A5%BF%E6%B9%96%E8%AE%BA%E5%89%91CTF-%E4%BA%8C/
0x3A=3*16+10=58
BASE58编码
上面运行时忘了摁回车…
>>> s='34avux4BwXYJzh1nHK1oG5xTKeBSCERZs4xC'
>>> t='123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz'
>>> flag=0
>>> for i in range(len(s)):
... flag=flag*58+t.index(s[i])
... flag
File "<stdin>", line 3
flag
^
SyntaxError: invalid syntax
>>> flag
0
>>> flag
0
>>> for i in range(len(s)):
... flag=flag*58+t.index(s[i])
...
>>> flag
108200298718158997245509125691632101258313020496600351308152445
>>> hex(flag)
'0x43554d544354467b3841736535425f31735f456135797e7e7e7d'
>>> from binascii import *
>>> a2b_hex('43554d544354467b3841736535425f31735f456135797e7e7e7d')
b'CUMTCTF{8Ase5B_1s_Ea5y~~~}'