經典排序算法 - JavaScript 實現
基本排序術語
- 穩定 : 若 a 原本在 b 前面,排序後 a 仍在 b 前面。
- 不穩定 : 若 a 原本在 b 前面,排序後 a 有可能在 b 後面。
- 內排序 : 所有排序過程都在內存中進行完。
- 外排序 : 因為數據量過於龐大,因此依靠外存 (磁盤,硬盤等等) 存儲並數據傳輸。
- 時間複雜度 : 算法所需的時間。
- 空間複雜度 : 算法所需的內存空間。
概覽
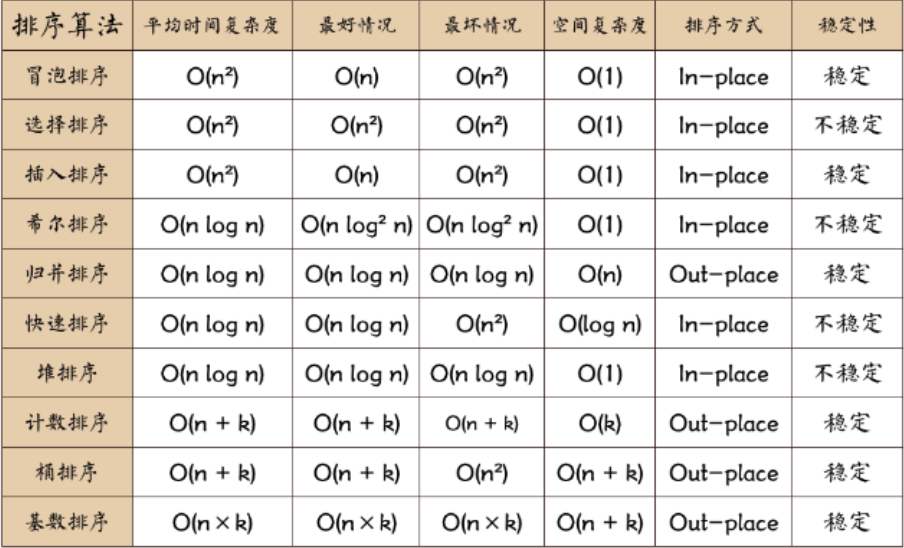
排序算法
Bubble sort 冒泡排序
冒泡排序的思想是最簡單直觀的,就是相當於相當於比較相鄰的兩個元素,如果前一個比後一個大,就要交換位置
。
- 代碼實現:
// Bubble sort
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function bubbleSort(arr) {
let len = arr.length;
for(let i = 0; i < len-1; i++) {
for(let j = i+1; j < len; j++) {
if(arr[i] > arr[j]) {
let tmp = arr[i]
arr[i] = arr[j]
arr[j] = tmp
}
}
}
return arr
}
arr = bubbleSort(arr)
console.log("After:", arr)
Quick sort 快速排序
快速排序可以說是非常重要的一個排序算法,因為其效率之高,而且使用到的分治思想也非常經典,所以理解快排還是很重要的。
快排使用到了分治的思想,基本思想如下:
- 得先從數列中選一個數作為基數(base)
- 分區,要把 > base 的放到 base 的右邊,<= base 的方到 base 的左邊
- 對左右區間重複執行 1,2,直到區間只為一個數
來看看實際上快排的具體執行機制:

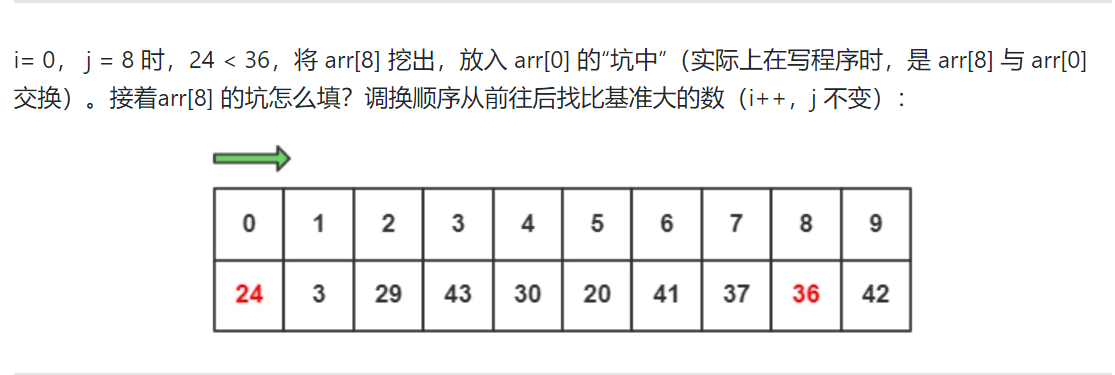


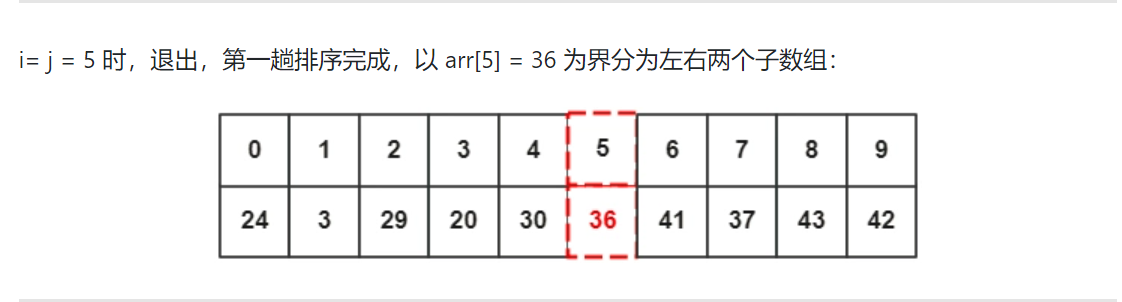

- 代碼實現:
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function quickSort(arr, i, j) {
if(i < j) {
let left = i
let right = j
let pivot = arr[left]
while(i < j) {
while(arr[j] >= pivot && i < j) {
// 從後往前找比pivot小的
j--
}
if(i < j) {
arr[i++] = arr[j]
}
while(arr[i] <= pivot && i < j) {
// 從前往後找比pivot大的
i++
}
if(i < j) {
arr[j--] = arr[i]
}
}
arr[i] = pivot
quickSort(arr, left, i-1)
quickSort(arr, i+1, right)
return arr
}
}
arr = quickSort(arr, 0, arr.length-1)
console.log("After:", arr)
Insertion sort 插入排序
插入排序的思想是,每一步將待排序的元素逐一插入到已經排好序的的有序序列中,直到所有元素都排序完畢。
在插入排序中,我們都先假設第 0 個數已經是個有序序列了,因此都是從第 1 個數開始判斷,每次都跟前一個元素比較,若發現小於前一個元素,就交換,直到大於等於某元素,也就意味找到了在前面的有序序列中,對當前元素合適的插入位置。
假設今天要排序的數列是 [8,15,20,45,17]。對 17 而言,因為 17 < 45,所以要交換,變成 [8,15,20,17,45],因為 17 < 20,所以要再交換,變成 [8,15,17,20,45],這時發現 17 > 15,不需要交換。當不需要與 15 交換時,也就意味著都不需要與 15 以前的數進行比較,因為前面肯定也都是有序的,既然都已經比 15 大了,也肯定比 15 以前的元素大。
- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function insertionSort(arr) {
// 默認第 0 個元素是有序的
// 所以從第 1 個元素開始往前慢慢插入
for(let i = 1; i < arr.length; i++) {
if(arr[i] < arr[i-1]) {
// 取出要被交換的元素
let guard = arr[i]
// 記住有敘數列的最後一個位置
let j = i - 1
while(j >= 0 && guard < arr[j]) {
arr[j + 1] = arr[j]
j--
}
arr[j + 1] = guard
}
}
return arr
}
arr = insertionSort(arr)
console.log("After:", arr)
Selection sort 選擇排序
選擇排序的思想就是,每次找到未排序序列中最小的元素,並放到排序序列的起始位置,直到未排序序列長度為 0。選擇排序因為比較耗時,所以其實很少實際被應用到。
- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function selectionSort(arr) {
let minIndex, tmp
for(let i = 0; i < arr.length - 1; i++) {
minIndex = i
for(let j = i + 1; j < arr.length; j++) {
if(arr[j] < arr[i]) {
minIndex = j
}
}
tmp = arr[i]
arr[i] = arr[minIndex]
arr[minIndex] = tmp
}
return arr
}
arr = selectionSort(arr)
console.log("After:", arr)
Shell sort 希爾排序
希爾排序可以說是插入排序的改良版,對於中等規模的數據表現還不錯。其實概念就是將待排序的數據先依 gap 進行分組(gap 依據觀察由我們自己定義),然後對每個分組作上面提到的插入排序,使各分組變為有序,gap 慢慢變小通常是縮小一半,直到 gap = 1 做最後一次插入排序。
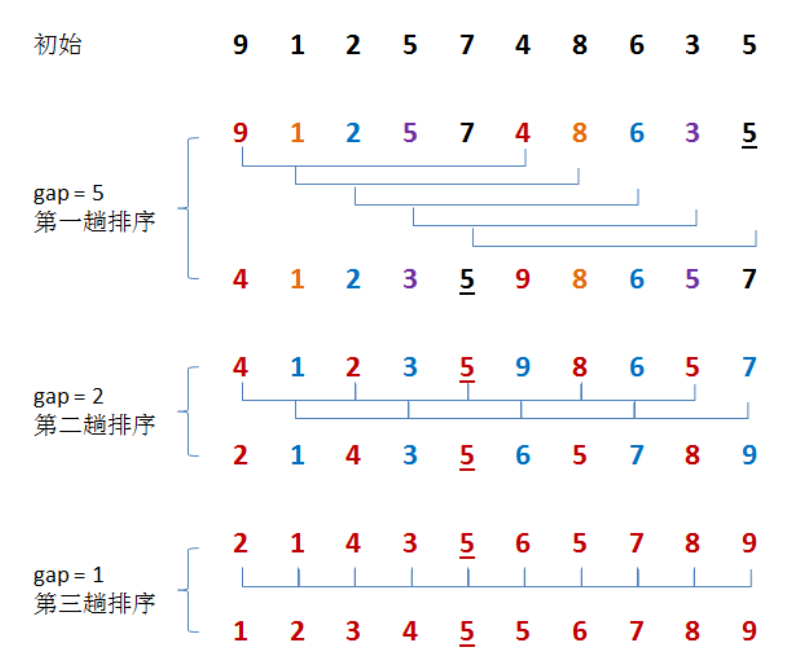
- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function shellSort(arr) {
var len = arr.length,
temp,
gap = 1;
while(gap < len/3) {
// 動態定義 gap
gap =gap*3+1;
}
for (gap; gap > 0; gap = Math.floor(gap/3)) {
for (var i = gap; i < len; i++) {
temp = arr[i];
for (var j = i-gap; j >= 0 && arr[j] > temp; j-=gap) {
arr[j+gap] = arr[j];
}
arr[j+gap] = temp;
}
}
return arr;
}
arr = shellSort(arr)
console.log("After:", arr)
Merge sort 歸併排序
歸併排序是一種通用的排序算法,是非常重要的算法。它採取分算法 (Divide and Conquer),是一個常用且重要的思想,由大名鼎鼎的 Jon Von Neumann 發明於 1945。
下面動圖非常清楚,是歸併排序的工作過程:
看完一個流式的示意圖,再來看看一個總體的示意圖,對 7 個數的數組 [38, 27, 43, 3, 9, 82, 10] 進行排序:
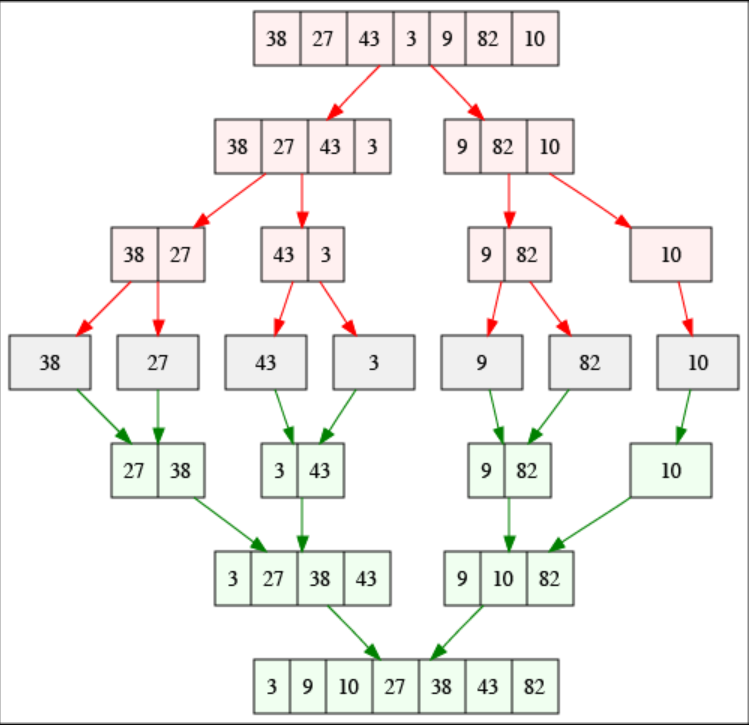
- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function mergeSort(arr) {
let len = arr.length
if(len < 2) {
return arr
}
let middle = Math.floor(len / 2)
let left = arr.slice(0, middle)
let right = arr.slice(middle, len)
return merge(mergeSort(left), mergeSort(right))
}
function merge(left, right) {
let [l, r] = [0, 0]
let res = []
while(l < left.length && r < right.length) {
if(left[l] < right[r]) {
res.push(left[l])
l++
}else {
res.push(right[r])
r++
}
}
res = res.concat(left.slice(l, left.length))
res = res.concat(right.slice(r, right.length))
return res
}
arr = mergeSort(arr)
console.log("After:", arr)
Heap sort 堆排序
堆排序也是使用上很常見的排序算法,不過要學會堆排序,首先還得先有一些預備知識:
預備知識
- 首先,堆是一個完全二叉樹。
- 完全二叉樹 : 除了葉節點層,其他每一層的每個節點都達到滿的狀態,且葉節點層所有節點都集中在左邊,只有在左邊已經滿了的狀態下,才能叉到右邊。
- 大頂堆 : 根結點為最大值,每個節點的值 >= 其子節點的值。
- 小頂堆 : 根結點為最小值,每個節點的值 <= 其子節點的值。
- 堆的存儲 : 在代碼實現上,通常用數組來實現堆的存儲。
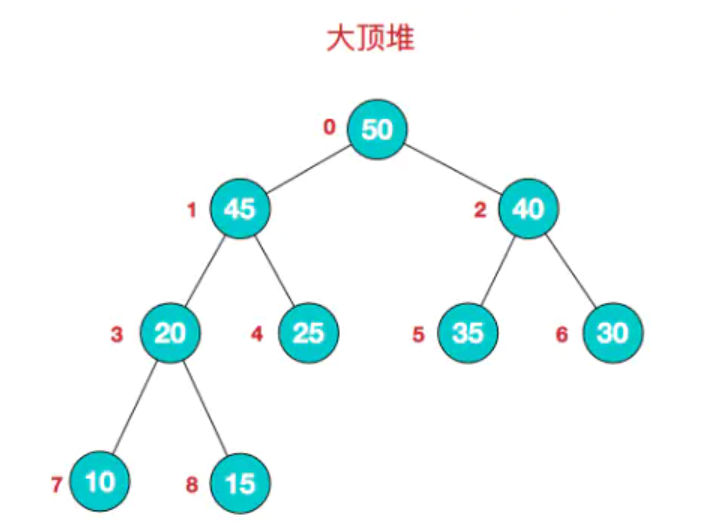

排序機制

現在要對上述的序列做堆排序,分為 3 步驟:
Step1
初始化大頂堆
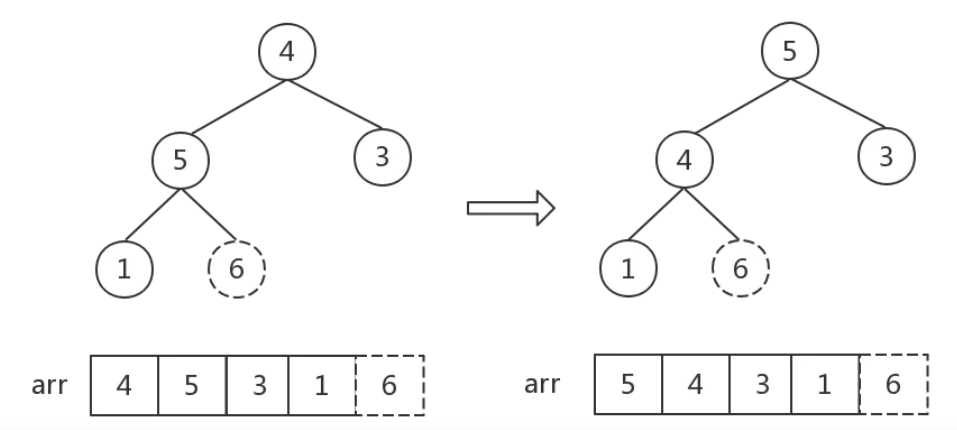
首先要先選取最後一個非葉節點 (這邊注意,我們只需要調整父子節點的關係,子節點之間我們無須關心)。設數組為 arr,則最後一個非葉節點得下標就是 i = Math.floor(arr.length / 2 - 1)。以上圖為例,i = 1,也就是節點 4。然後,如下圖中虛線框所示,我們找到三個數字的最大值,與父節點交換。

接著,下標依次遞減,也就是說,從最後一個非葉節點,由下往上遍歷所有非葉節點,然後所做的操作都跟剛剛一樣,就是要找到父子節點 (共計 3 個節點) 中最大那個,並跟父節點交換。

這邊要特別注意!如上圖,經過這一步,我們交換 1,6,但是可以看到,[1,5,4] 組成的堆不符合大頂堆的性質了,所以又需要再做一次調整。所以,要注意的地方就在於,每次交換完後,都要檢查看看子節點所組成的堆是否滿足大頂堆的性質。
在第一步的最後,還要將根結點與最後一個節點交換。

Step2
第二步要做的如下,除去最後一個節點,將其餘節點組成的新堆組成大頂堆,這時,根結點應該是次大的值,然後再與最後一個節點交換。

Step3
第三步開始,就是一直重複第二步,直到堆中的元素只剩一個。
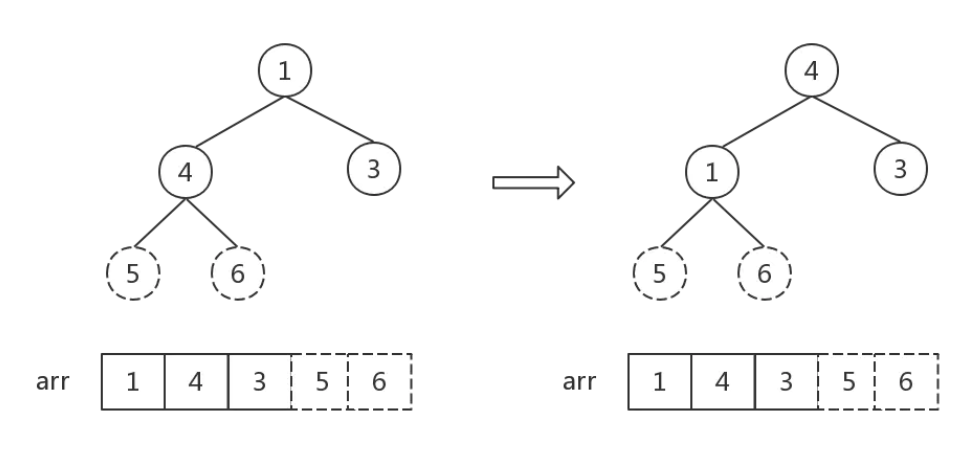
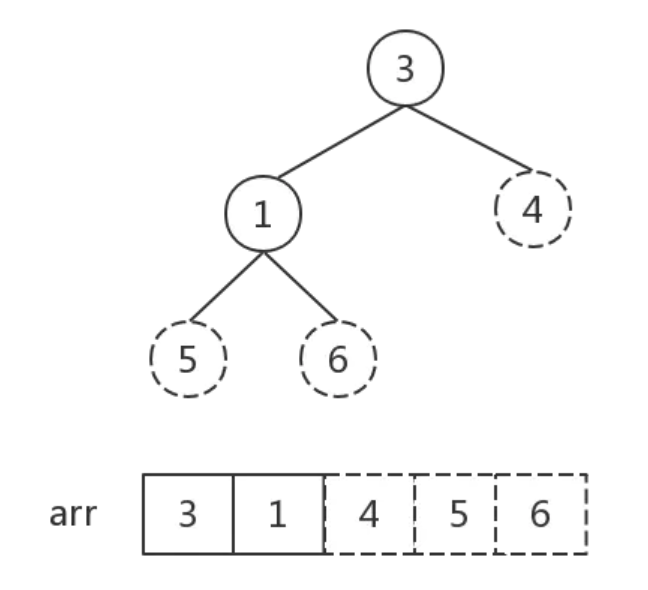

至此,堆中個數 = 1,排序完成。
- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
// 交換兩個節點
function swap(H, i, j) {
let temp = H[i]
H[i] = H[j]
H[j] = temp
}
// 將 i 節點以下的節點整理成大頂堆
function adjustHeap(H, i, length) {
let temp = H[i] // 當前父節點
/**
* j = 2*i+1 : 對於當前父節點索引 i,其左子節點的索引 j
* j < length : 對節點 i 以下的節點都作調整
*/
for(let j = 2*i+1; j < length; j = 2*j+1) {
temp = H[i] // 每次比較的父節點
if(j+1 < length && H[j] < H[j+1]) {
j++ // 找出對於當前父節點的兩個子節點中,比較大的那個的索引 (j)
}
// 將當前父節點與較大的子節點比較,若 父 < 子 則交換,反之則跳出
if(temp < H[j]) {
swap(H, i, j)
i = j // 交換了的話,每次比較的父節點的索引 i 要變成 j
}else{
break
}
}
}
// 堆排序主方法
function heapSort(H) {
// 初始化大頂堆
for(let i = Math.floor(H.length / 2 - 1); i >= 0; i--) {
adjustHeap(H, i, H.length)
}
// 堆排序
for(let i = H.length - 1; i > 0; i--) {
swap(H, 0, i) // 根結點與最後一個節點交換
adjustHeap(H, 0, i)
}
return H
}
arr = heapSort(arr)
console.log("After:", arr)
Counting sort 計數排序
計數排序是一個比較特別的排序算法,利用的是數組的下標 (index) 天然有序的特徵。不過計數排序有一個條件,就是要知道數列的範圍。作法其實很簡單,假設今天已知要排序的數列範圍為 [1, 10],那我們就要新開一個數組 C 大小就是 10那,初始化全部為 0。然後開始遍歷我們的數列,在 C 中的每一位存相應的次數在該數列中出現的次數,那到時候我們就只要根據 C 輸出相應位個次數就好了。
計數排序因為不需要做任何比較,所以比起其他排序算法來說確實很快,但缺點也很明顯,首先你得知道待排序數列的範圍,而且對於波動大的數列,將會占用掉很多的空間。
- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
// 已知待排序數列範圍是 1~10
function countSort(arr) {
res = []
let C = new Array(arr.length).fill(0)
for(let i = 0; i < C.length; i++) {
let count = 0
check = i + 1
for(let j = 0; j < arr.length; j++) {
if(arr[j] == check) {
count++
}
}
C[i] = count
}
for(let i = 0; i < C.length; i++) {
if(C[i] == 0) {
continue
}else{
let count = C[i]
while(count > 0) {
res.push(i + 1)
count--
}
}
}
return res
}
arr = countSort(arr)
console.log("After:", arr)
Bucket sort 桶排序
桶排序相當於是計數排序的升級版,思想就是把要排序的數列分組放到一些桶中,然後對每個桶分別先進行排序,且注意,每個桶是知道區間的,且按區間大小排好的,那麼很自然的,各桶中的排序通常就是使用計數排序來排序。
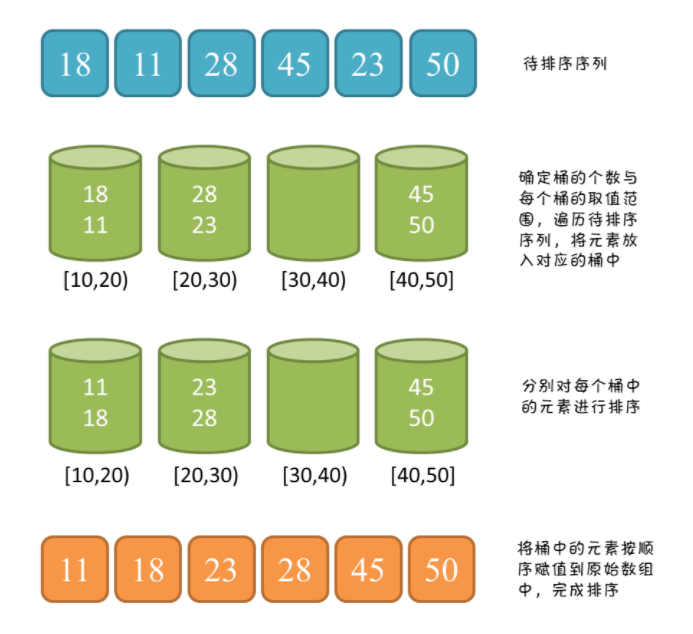
通常,為了使桶排序效率較好,我們要做到以下兩點:
- 希望能將待排序的 N 個數盡可能均勻地分配到 K 個桶中
- 因應 1. 盡可能將 K 增大
- 至於每桶中要用什麼排序算法,當然也是可以根據場景需求自行決定的
- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function bucketSort(arr, bucketSize) {
res = []
if(arr.length < 2) {
return arr
}
// 找到數列的最大值和最小值
let minVal = arr[0]
let maxVal = arr[0]
for(let i = 0; i < arr.length; i++) {
if(arr[i] < minVal) {
minVal = arr[i]
}
if(arr[i] > maxVal) {
maxVal = arr[i]
}
}
// 初始化桶
let bucketCnt = Math.floor((maxVal - minVal) / bucketSize) + 1
let buckets = new Array(bucketCnt)
for(let i = 0; i < buckets.length; i++) {
buckets[i] = []
}
// 將數據分配到各個桶中
for(let i = 0; i < arr.length; i++) {
buckets[Math.floor((arr[i] - minVal) / bucketSize)].push(arr[i])
}
// 各桶逐一排序
for(let i = 0; i < buckets.length; i++) {
buckets[i] = insertionSort(buckets[i]) // 這邊桶中的排序使用插入排序
for(let j = 0; j < buckets[i].length; j++) {
res.push(buckets[i][j])
}
}
return res
}
function insertionSort(arr) {
// 默認第 0 個元素是有序的
// 所以從第 1 個元素開始往前慢慢插入
for(let i = 1; i < arr.length; i++) {
if(arr[i] < arr[i-1]) {
// 取出要被交換的元素
let guard = arr[i]
// 記住有敘數列的最後一個位置
let j = i - 1
while(j >= 0 && guard < arr[j]) {
arr[j + 1] = arr[j]
j--
}
arr[j + 1] = guard
}
}
return arr
}
arr = bucketSort(arr, 4)
console.log("After:", arr)
Radix sort 基數排序
基數排序的思路是按照每個數的位數進行排序的。先對個位數的大小排序,再來換十位數,以此類推。而在某一位數進行排序時,是用桶來排序的,所以需要有 10 個桶 (數字有 0~9)。將相同數值的數字放到相應的桶中,然後再依序取出,這樣對於一位的排序就算完成。

- 代碼實現
let arr = [1,3,2,5,6,10,9,8,7,4]
console.log("Before:", arr)
function radixSort(arr) {
let len = arr.length
let res = []
let counter = []
let mod = 10
let dev = 1
// 找出最大的數
let maxNum = arr[0]
for(let i = 0; i < len; i++) {
if(arr[i] > maxNum) {
maxNum = arr[i]
}
}
// 找出最大的數的位數
let maxDigit = 0
while(maxNum != 0) {
maxNum = parseInt(maxNum / 10)
maxDigit++
}
for(let i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
for(let j = 0; j < len; j++) {
let bucket = parseInt((arr[j] % mod) / dev)
if(counter[bucket] == null) {
counter[bucket] = []
}
counter[bucket].push(arr[j])
}
let index = 0
for(let j = 0; j < counter.length; j++) {
let value = null
if(counter[j] != null) {
while((value = counter[j].shift()) != null) {
arr[index++] = value
}
}
}
}
return arr
}
arr = radixSort(arr)
console.log("After:", arr)
