第七章 动态规划
递推求解
我们来看一个知名的数列一斐波那契数列。 这个数列是这样定义的,它的第一个数是1,第二个数也是1,其后的每一个数都是前两个数的和,即这样一个数列: 1、1、2、3、5、8、…这样,只要我们确定了这个数列的前两个数,那么后面的每一个数都能经过一次次的累加得到。即,当我们知道这个数列的开头几个数字,并确定它的递推规则,只需通过重复的递推就能得到这个数列的每一个数。
利用递推解决问题,我们就要模仿求斐波那契数列的过程。首先,确定几个规模较小的问题答案。然后考虑如何由这几个规模较小的答案推得后面的答案。一旦有了递推规则和数列初始的几个值,计算机程序就能帮助我们求解数列后面的所有数字,我们的问题也得到了解决。
Problem 1


这个问题就是一个典型的递推问题。若我们把N分别等于1、2、3…的答案依次排列为一个数列,我们即需求这个数列每一个数的值。我们定义f[n]为数列中第n个数,同时F[n]为台阶总数为n时的上台阶方式总数。首先,当数据规模较小时我们可以直接得到答案,如F[1]=1, F[2]=2。其次,我们必须确定数列间的递推关系。当n大于2时,我们考虑每种上台阶方式的最后一步,由于只有两种行走的方法,因此它只可能是从n-1阶经过一步走到n阶,或者从n-2阶经过二步走到n阶。我们分别考虑这两种走法,即我们将此时所有的上楼梯方式按照最后一步走法的不同分成两类,分别确定这两类的上楼梯方式数目。经n-1阶到达n阶,因为其最后一步是确定的,所以上楼梯方式数量与原问题中到达n-1阶的方式数量相同,同为F[n-1];同理,经n-2阶到达n阶,其上楼梯方式数量与原问题中到达n-2阶的方式数量相同,同为F[n- 2]。这样,我们就确定了达到n阶楼梯总的上楼方式个数为F[n- 1]和F[n-2]的和, 即F[n]=F[n- 1]+F[n-2]。这就是这个数列的递推关系。由初始值F[1]=1, F[2]=2,我们就能推得所有F[m]的值。
#include <stdio.h>
long long F[91]; //F数组保存数列的每一个值,由于数值过大,我们需要使用long long类型
int main() {
F[1]=1;
F[2]=2; //数列初始值
for (int i=3;i<=90;i++)
F[i]=F[i-1]+F[i-2]; //递推求得数列的每一个数字
int n;
while (scanf("%d",&n) !=EOF) {
printf("%lld\n",F[n]);
}
return 0;
}
Problem 2

同样的,在该例中我们也容易得到规模较小时的错装方式数量。如n为1时,数量为0; n为2时数量为1。我们按照n的取值顺序将所有的错装方式数量排列为一个数列,同样用F[n]表示数列里第n个数的取值,F[n]同时代表n个信封的错装方式总数,我们确定该数列的递推关系。当n大于3时,我们考虑n封信全部装错的情况。将信封按顺序由1到n编号。在任意一种错装方案中,假设n号信封里装的是k号信封的信,而n号信封里的信则装在m号信封里。我们按照k和m的等值与否将总的错装方式分为两类。
若k不等于m,交换n号信封和m号信封的信后,n号信封里裝的恰好是对应的信,而m号信封中错装k号信封里的信,即除n号信封外其余n-1个信封全部错装,其错装方式等于F[n-1],又由于m的n-1个可能取值,这类错装方式总数为(n-1) * F[n-1]。也可以理解为,在n-1个信封错装的F[n-1]种方式的基础上,将n号信封所装的信与n- 1个信封中任意一个信封(共有n-1中选择)所装的信做交换后,得到所有信封全部错装的方式数。
另一种情况,若k等于m,交换n号信封和m号信封的信后,n号信封和m号信封里装的恰好是对应的信,这样除它们之外剩余的n-2个信封全部错装,其错装方式为F[n-2],又由于m的n-1个取值,这类错装方式总数为(n-1) * F[n-2]。也可以理解为,在n-2个信封全部错装的基础上,交换最后两个信封的信(n号信封和1到n-1号信封中任意一个,共有n-1种选择),使所有的信封全部错装的方式数。
综上所述,F[n]=(n-1) * F[n- 1]+(n-1) * F[n-2]。这就是有名的错排公式。
#include <stdio.h>
long long F[21]; //数值较大选用long long
int main() {
F[1]=0;
F[2]=1; //初始值
for(int i=3;i<=20;i++)
F[i]=(i-1)*F[i-1]+ (i-1)*F[i-2]; //递推求得数列每-一个数字
int n;
while (scanf("%d", &n)!=EOF) {
printf("%lld\n",F[n]);
}
return 0;
}
递推求解问题,根据输入的顺序,其答案往往排列成一个数列。为了求得数列中的每一个数字,我们首先得到输入规模较小时的答案,即数列开头的几个数字。分析问题,将每一个问题都分割成规模较小的几个问题,分割过程中要做到不遗漏不重复,并确定它们的关系从而得到递推关系式,利用它求出每一个输入所对应的答案。
最长递增子序列(LIS)
最长递增子序列是动态规划中最经典的问题之一,总结一下,求最长递增子序列的递推公式为:
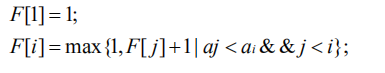
有序列{a1,a2…an},我们求其最长递增子序列长度。按照递推求解的思想,我们用F向代表若递增子序列以a结束时它的最长长度。当i较小,我们容易直接得出其值,如F[1]= 1。那么,如何由已经求得的F[i]值推得后面的值呢?假设,F[1]到F[x-1]的值都已经确定,注意到,以ax结尾的递增子序列,除了长度为1的情况,其它情况中, ax都是紧跟在一个由ai(i<x)组成递增子序列之后。要求以a结尾的最长递增子序列长度,我们依次比较ax与其之前所有的ai(i <x),若ai小于ax,则说明ax可以跟在以ai结尾的递增子序列之后,形成一个新的递增子序列。又因为以a结尾的递增子序列最长长度已经求得,那么在这种情况下,由以ai结尾的最长递增子序列再加上ax得到的新的序列,其长度也可以确定,取所有这些长度的最大值,我们即能得到F[x]的值。特殊的,当没有ai(i <x)小于ax,,那么以ax结尾的递增子序列最长长度为1。即F[x]=max{1, F[i]+1| ai< ax&&i<x};

由题意不难看出,要求最多能够拦截多少枚导弹,即在按照袭击顺序排列的导弹高度中求其最长不增子序列。所谓不增子序列,即子序列中排在前面的数字不比排在后面的数字小。求最长不增子序列的原理与求最长递增子序列的原理完全一致,只是递推关系相应的发生一些变化,递推关系如下:
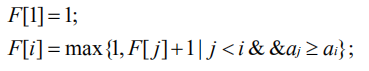
#include <stdio.h>
int max(int a,int b) {
return a > b? a:b;} //取最大值函数
int list[26]; //按袭击事件顺序保存各导弹高度
int dp[26]; //dp[i]保存以第i个导弹结尾的最长不增子序列长度
int main(){
int n;
while(scanf("%d",&n) !=EOF) {
for(int i=1;i<=n;i++){
scanf("%d",&list[i]);
}
for (int i=1;i<=n;i++) {
//按照袭击时间顺序确定每一个dp[i]
int tmax=1; //最大值的初始值为1,即以其结尾的最长不增子序列长度至少为1
for(int j=1;j<i;j++){
//遍历其前所有导弹高度
if (list[j] >= list[i]) {
//若j号导弹不比当前导弹低
tmax=max(tmax, dp[j] + 1); //将当前导弹排列在以j号导弹结尾的最长不增子序列之后,计算其长度dp[j]+1, 若大于当前最大值,则更新最大值
}
}
dp[i]=tmax; //将dp[i]保存为最大值
}
int ans=1;
for(int i=1;i<=n;i++){
ans=max(ans,dp[i]);
} //找到以每一个元素结尾的最长不增子序列中的最大值,该最大值即为答案
printf("%d\n",ans);
}
return 0;
}
其时间复杂度为O (n*n),空间复杂度为O (n)。
由上例的分析过程可知,最长递增子序列问题的求解思想,不仅可以用来解决单纯的最长递增子序列问题,也可以经过类比来求解其它大小关系确定的子序列最长长度。
最长公共子序列(LCS)
有两个字符串S1和S2,求一个最长公共子串,即求字符串S3,它同时为S1和S2的子串,且要求它的长度最长,并确定这个长度。这个问题被我们称为最长公共子序列问题。
与求最长递增子序列一样,我们首先将原问题分割成一些子问题,我们用dp[i][j]表示S1中前i个字符与S2中前j个字符分别组成的两个前缀字符串的最长公共子串长度。显然的,当i、j较小时我们可以直接得出答案,如dp[0][i]必等于0。那么,假设我们已经求得dp[i][j] (0<=i<x,0<=j<y)的所有值,考虑如何由这些值继而推得dp[x][y],求得S1前x个字符组成的前缀子串和S2前y个字符组成的前缀子串的最长公共子序列长度。若S1[x]==S2[y],即S1中的第x个字符和S2中的第y个字符相同,同时由于他们都是各自前缀子串的最后一个字符,那么必存在一个最长公共子串以S1[x]或S2[y]结尾,其它部分等价于S1中前x-1个字符和S2中前y-1个字符的最长公共子串。所以这个子串的长度比dp[x-1][y-1]又增加1,即dp[x][y] =dp[x-1][y-1]+1。相反的,若S1[x]!= S2[y],此时其最长公共子串长度为S1中前x-1个字符和S2中前y个字符的最长公共子串长度与S1中前x个字符和S2中前y-1个字符的最长公共子串长度的较大者,即在两种情况下得到的最长公共子串都不会因为其中一个字符串又增加了一个字符长度发生改变。综上所述,dp[x][y]=max {dp[x-1][y],dp[x][y-1]}。
最长公共子序列问题的递推条件:
假设有两个字符串S1和S2,其中S1长度为n,S2长度为m,用dp[i][j]表示S1前i个字符组成的前缀子串与S2前j个字符组成的前缀子串的最长公共子串长度,那么:
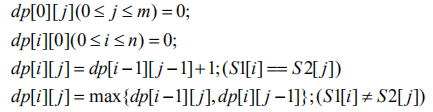
由这样的递推公式和显而易见的初始值,我们即能依次求得各dp[i][j]的值,最终dp[n][m]中保存的值即为两个原始字符串的最长公共子序列长度。

#include <stdio.h>
#include <string.h>
int dp[101][101];
int max(int a,int b) {
return a>b? a:b;} //取最大值函数
int main(){
char S1[101],S2[101];
while(scanf("%s%s",S1,S2)!=EOF) {
int L1=strlen(S1);
int L2=strlen(S2); //依次求得两个字符串的长度
for(int i=0;i<=L1;i++) dp[i][0]=0;
for(int j=0;j<=L2;j++) dp[0][j]=0; //初始值
for(int i=1;i<=L1;i++){
for (int j=1;j<=L2;j++) {
//二重循环依次求得每个dp[i][j]值
if(S1[i-1]!=S2[j-1])
//因为字符串数组下标从0开始,所以第i个字符位置为S1[i-1],若当前两个字符不相等
dp[i][j]=max(dp[i][j-1],dp[i-1][j]); //dp[i][j]为dp[i][j-1]和dp[i-1][j]中较大的一个
else dp[i][j]=dp[i-1][j-1]+1; //若它们相等,则dp[i][j]比dp[i-1][j-1]再加一
}
}
printf("%d\n",dp[L1][L2]);
}
return 0;
}
其时空复杂度都是O(L1 * L2),其中L1和L2分别为两个字符串的长度。
状态与状态转移方程
回顾两种经典问题的算法模式,我们都先定义了一个数字量,如最长递增子序列中用dp[i][j]表示以序列中第i个数字结尾的最长递增子序列长度和最长公共子序列中用dp[i][j]表示的两个字符串中前i、j个字符的最长公共子序列,我们就是通过对这两个数字量的不断求解最终得到答案的。这个数字量就被我们称为状态。状态是描述问题当前状况的一个数字量。
首先,它是数字的,是可以被抽象出来保存在内存中的。
其次,它可以完全的表示一个状态的特征,而不需要其他任何的辅助信息。
最后,也是状态最重要的特点,状态间的转移完全依赖于各个状态本身,如最长递增子序列中,dp[x]的值由dp[i] (i<x)的值确定。
若我们在分析动态规划问题的时候能够找到这样一个符合以上所有条件的状态,那么多半这个问题是可以被正确解出的。这就是为什么人们常说,做DP题的关键,就是寻找一个好的状态。
动态规划问题分析举例
Problem 1

在选定的最优方案中,每对物品都是重量相邻的一对物品。
在得出这个结论后,我们设计描述该问题的状态。首先将所有物品按照重量递增排序,并由1到n编号。设dp[i][j]为在前j件物品中选择i对物品时最小的疲劳度,那么根据物品j和物品j-1是否被配对选择,该状态有两个来源:若物品j和物品j-1未被配对,则物品j一定没被选择,所以dp[i][j]等价于dp[i][j-1];若物品j和物品j-1配对,则dp[i][j]为dp[i-1][j-2]再加上这两件物品配对后产生的疲劳度,即前j-2件物品配成的i-1对再加上最后两件配成的一对物品,共得到i对物品。
初始时,dp[0]为 0,即不选择任何一对物品时,疲劳度为0。
综上所述,其状态转移方程为(设经过排序后第i件物品重量为list[i]):
#include <stdio.h>
#include <algorithm>
using namespace std;
#define INF 0x7ffffff //预定义最大的int取值为无穷
int list[2001]; //保存每个物品重量
int dp[1001][2001]; //保存每个状态
int main(){
int n,k;
while (scanf("%d%d",&n, &k) != EOF) {
for(int i=1;i<=n;i++){
scanf("%d", &list[i]);
}
sort(list+1,list+1+n); //使所有物品按照重量递增排序
for(int i=1;i<=n;i++) //初始值
dp[0][i]=0;
for(int i=1;i<=k;i++){
//递推求得每个状态
for(int j=2*i;j<=n;j++){
if(j>2*i)
/*若j>2*i则表明,最后两个物品可以不配对,即前j-1件物品足够
配成i对,dp[i][j]可以由dp[i][j-1]转移而来,其值先被设置为dp[i][j-1]*/
dp[i][j]=dp[i][j-1];
else
dp[i][j]=INF;
/*若j==2*i,说明最后两件物品必须配对,否则前j件物品配不
成对,所以其状态不能由dp[i][j-1]转移而来,dp[i][j]先设置为正无穷*/
if (dp[i][j] > dp[i-1][j-2] + (list[j]-list[j-1])*(list[j]-list[j-1]))
/*若dp[i][j]从dp[i-1][j-2]转移而来时,其值优于之前确定的
正无穷或者由dp[i][j-1]转移而来的值时,更新该状态*/
dp[i][j]=dp[i-1][j-2]+(list[j]-list[j-1])*(list[j]-list[j-1]); //更新
}
}
printf("%d\n", dp[k][n]);
}
return 0;
}
Problem 2

本题大意:有一堆柑橘,重量为0到2000,总重量不大于2000。要求我们从中取出两堆放在扁担的两头且两头的重量相等,问符合条件的每堆重量最大为多少。没有符合条件的分堆方式则输出-1。
首先,我们只考虑柑橘重量为非0的情况。
因为本题要求解的是重量相等的两堆柑橘中每堆的最大重量,并且在堆放过程中,由于新的柑橘被加到第一堆或者第二堆,两堆之间的重量差会动态发生改变,所以我们设状态dp[i][j]表示前i个柑橘被选择后(每个柑橘可能放到第一堆或者第二堆)后,第一堆比第二堆重j时(当j为负时表示第二堆比第一堆重),两堆的最大总重量和。
初始时,dp[0][0]为 0,即不往两堆中加任何柑橘时,两堆最大总重量为0;dp[0][j] (j不等于0)为负无穷,即其它状态都不存在。根据每一个新加入的柑橘被加入到第一堆或者第二堆或者不加到任何堆,设当前加入柑橘重量为list[i], 这将造成第一堆与第二堆的重量差增大list[i]或减小list[i]或者不变,我们在它们之中取最大值,其状态转移为:
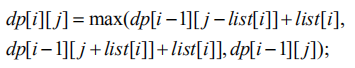
当根据该状态转移方程求出所有的状态后,状态dp[n][0]/2即是所求。
我们再来考虑柑橘重量包含0的情况,当在不考虑柑橘重量为0,推得dp[n][0]为正数时,柑橘重量为0的柑橘将不对答案造成任何影响,固在这种情况时可直接排除重量为0的柑橘。当在不考虑柑橘重量为0,推得dp[n][0]为0时,即不存在任何非0的组合使两堆重量相等。此时,若存在重量为0的柑橘,则可组成两堆重量为0的柑橘(至少有一个柑橘重量为0),它们重量相等;否则,将不存在任何分堆方式,输出-1。
#include <stdio.h>
#define OFFSET 2000
/*因为柑橘重量差存在负数的情况,即第一堆比第二堆轻,所以在计算重量差对应的数
组下标时加上该偏移值,使每个重量差对应合法的数组下标*/
int dp[101][4001]; //保存状态
int list[101]; //保存柑橘数量
#define INF 0x7ffffff //无穷
int main(){
int T;
int cas=0; //处理的Case数,以便输出
scanf("%d",&T); //输入要处理的数据组数
while (T--!=0) {
//T次循环
int n;
scanf("%d",&n);
bool HaveZero =false; //统计是否存在重量为0的柑橘
int cnt=0;//t数器,记录共有多少个重量非零的柑橘
for (int i=1;i<=n;i++) {
//输入n个柑橘重量
scanf("%d",&list[++cnt]);
if(list[cnt]==0) {
//若当前输入柑橘重量为
cnt --; //去除这个柑橘
HaveZero=true; //并记录存在重量为0的柑橘
}
}
n=cnt;
for (int i=-2000;i <= 2000;i++) {
dp[0][i+OFFSET]=-INF;
} //初始化,所有dp[0][i]为负无穷。注意要对重量差加上OFFSET后读取或调用
dp[0][0+OFFSET]=0; //dp[0][0]为0
for(int i=1;i<=n;i++){
//遍历每个柑橘
for (int j=-2000;j<=2000;j ++) {
//遍历每种可能的重量差
int tmp1=-INF, tmp2=-INF; //分别记录当前柑橘放在第一堆或第二堆时转移得来的新值若无法转移则为-INF
if (j + list[i] <= 2000 && dp[i-1][j + list[i] + OFFSET] !=-INF) {
//当状态可以由放在第一堆转移而来时
tmp1=dp[i-1][j+list[i]+OFFSET]+list[i]; //记录转移值
}
if (j - list[i] >=-2000 &&dp[i-1][j-list[i]+OFFSET]!=-INF) {
//当状态可以由放在第二堆转移而来时
tmp2=dp[i-1][j-list[i]+OFFSET]+list[i]; //记录该转移值
}
if (tmp1 < tmp2) {
tmp1=tmp2;
} //取两者中较大的那个,保存至tmp1
if (tmp1 < dp[i-1][j+OFFSET]) {
//将tmp1与当前柑橘不放入任何堆即状态差不发生改变的原状态值比较,取较大的值保存至tmp1
tmp1=dp[i-1][j+OFFSET];
}
dp[i][j+OFFSET]=tmp1; //当前值状态保存为三个转移来源转移得到的新值中最大的那个
}
}
printf("Case %d: ",++cas);//按题目输出要求输出
if (dp[n][0+OFFSET]==0) {
//dp[n][0]为0
puts( HaveZero==true ? "0" : "-1");//根据是否存在重量为0的柑橘输出0或-1
}
else printf(" %d\n", dp[n][0+OFFSET]/2); //否则输出dp[n][0]/2
}
return 0;
}
背包问题
Problem 1

首先我们将这个问题抽象:有一个容量为V的背包,和一些物品。这些物品分别有两个属性,体积w和价值v,每种物品只有一个。要求用这个背包装下价值尽可能多的物品,求该最大价值,背包可以不被装满。因为最优解中,每个物品都有两种可能的情况,即在背包中或者不存在(背包中有0个该物品或者1个),所以我们把这个问题称为0-1背包问题。在该例中,背包的容积和物品的体积等效为总共可用的时间和采摘每个草药所需的时间。
在众多方案中求解最优解,是典型的动态规划问题。为了用动态规划来解决该问题,我们用dp[i][j]表示在总体积不超过j的情况下,前i个物品所能达到的最大价值。初始时,dp[0][j] (0<=j<=V)为 0。依据每种物品是否被放入背包,每个状态有两个状态转移的来源。若物品i被放入背包,设其体积为w,价值为v,则dp[i][j] =dp[i- 1][j-w]+v。即在总体积不超过j-w时前i-1件物品可组成的最大价值的基础上再加上i物品的价值v;若物品不加入背包,则dp[i][j] = dp[i-1][j],即此时与总体积不超过j的前i-1件物品组成的价值最大值等价。选择它们之中较大的值成为状态dp[i][j]的值。综上所述,0-1 背包的状态转移方程为:
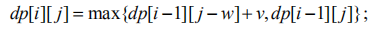
转移时要注意,j-w的值是否为非负值,若为负则该转移来源不能被转移。
#include <stdio.h>
#define INF 0x7fffffff
int max(int a,int b) {
return a > b ? a: b;} //取最大值函数
struct E{
//保存物品信息结构体
int w; //物品的体积
int v; //物 品的价值
}list[101];
int dp[101][1001]; //记录状态数组,dp[i][j]表示前i个物品组成的总体积不大于的最大价值和
int main(){
int s,n;
while(scanf("%d%d",&s,&n) !=EOF) {
for(int i=1;i<=n;i++){
scanf("%d%d",&list[i].w,&list[i].v);
}
for(int i=0;i<=s;i++){
dp[0][i]=0;
} //初始化状态
for (int i=1;i<=n;i++) {
//循环每一个物品
for (int j=s;j>=list[i].w;j--) {
//对s到list[i].w的每个j,状态转移来源为dp[i-1][j]或dp[i-1][j-list[i].w]+list[i].v, 选择其中较大的值
dp[i][j]=max(dp[i-1][j],dp[i-1][j-list[i].w]+list[i].v);
for (int j=list[i].w-1;j>=0;j--)
//对list[i].w-1到0的每个j,状态仅能来源于dp[i-1][j], 固直接赋值
dp[i][j]=dp[i-1][j];
}
}
printf("%d\n",dp[n][s]);
}
return 0;
}
观察状态转移的特点,我们发现dp[i][j]的转移仅与dp[i-1][j-list[i].w]和dp[i-1][j]有关, 即仅与二维数组中本行的上一行有关。根据这个特点,我们可以将原本的二维数组优化为一维,并用如下方式完成状态转移:
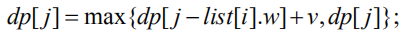
为了保证状态正确的转移,我们必领保证在每次更新中确定状态dp[j]时,dp[j]和dp[i-1][j-list[i].w]尚未被本次更新修改。考虑到j-list[i].w<j, 那么在每次更新中倒序遍历所有j的值,就能保证在确定dp[j]的值时,dp[j- list[i].w]的值尚未被修改,从而完成正确的状态转移。
#include <stdio.h>
#define INF 0x7fffffff
int max(int a,int b){
return a>b?a:b;}//取最大值函数
struct E {
//表示物品结构体
int w;
int v;
}list[101];
int dp[1001];
int main(){
int s,n;
while (scanf("%d%d",&s,&n) !=EOF) {
for(int i=1;i<=n;i++){
scanf("%d%d",&list[i].w,&list[i].v);
}
for(int i=0;i<=s;i++){
dp[i]=0;
} //初始值
for(int i=1;i<=n;i++){
for (int j=s;j>=list[i].w;j--) {
//必须倒序更新每个dp[j]的值,j小于list[i].w的各dp[j]不作更新,保持原值,即等价于dp[i][j],dp[i-1][j]
dp[j]=max(dp[j],dp[j-list[i].w]+list[i].v); //dp[j]在原值和dp[j-list[i].w]+list[i].v中选取较大的那个
}
}
printf("%d\n",dp[s]);
}
return 0;
}
分析求解0-1背包问题的算法复杂度。其状态数量为n * s,其中n为物品数量,s为背包的总容积,状态转移复杂度为O(1),所以综合时间复杂度为O(n*s)。经优化过后的空间复杂度仅为O(s) (不包括保存物品信息所用的空间)。0-1背包问题是最基本的背包问题,其它各类背包问题都是在其基础上演变而来。牢记0-1背包的特点:每一件物品至多只能选择一件,即在背包中该物品数量只有0和1两种情况。
接着,我们扩展0-1背包问题,使每种物品的数量无限增加,便得到完全背包问题:有一个容积为V的背包,同时有n个物品,每个物品均有各自的体积w和价值v,每个物品的数量均为无限个,求使用该背包最多能装的物品价值总和。
我们先按照0-1背包的思路试着求解该问题。设当前物品的体积为w,价值为v,考虑到背包中最多存放V/w件该物品,我们可以将该物品拆成V/w件,即将当前可选数量为无限的物品等价为V/w件体积为w、价值为v的不同物品。对所有的物品均做此拆分,最后对拆分后的所有物品做0-1背包即可得到答案。但是,这样的拆分将使物品数量大大增加,其时间复杂度为:
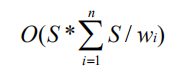
可见,当S较大同时每个物品的体积较小时其复杂度会显著增大,固将该问题转化为0-1背包的做法较不可靠。但是由该解法可窥见0-1背包的重要性,很多背包问题均可以推到0-1背包上来。
Problem 2



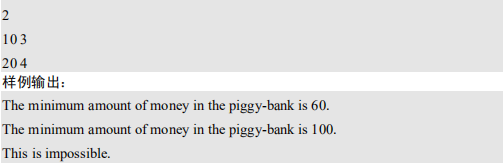
题目大意:有一个储蓄罐,告知其空时的重量和当前重量,并给定一些钱币的价值和相应的重量,求储蓄罐中最少有多少现金。
由于每个钱币的数量都可以有任意多,所以该问题为完全背包问题。但是在该例中,完全背包有两处变化,首先,要求的不再是最大值,而变为了最小值,这就要求我们在状态转移时,在dp[j]和dp[j-list[i].w]+list[i].v 中选择较小的转移值;其次,该问题要求钱币和空储蓄罐的重量恰好达到总重量,即在背包问题中表现为背包恰好装满,在前文中我们已经讨论了0-1背包的此类变化,我们只需变化dp[i]的初始值即可。
#include <stdio.h>
#define INF 0x7fffffff
int min(int a,int b){
return a<b?a:b;}//取最小值函数
struct E {
//代表钱币结构体
int w; //重量
int v; //价值
}list[501];
int dp[10001]; //状态
int main() {
int T;
scanf("%d",&T); //输入测试数据组数
while (T--) {
//T次循环,处理T组数据
int s,tmp;
scanf("%d%d",&tmp,&s); //输入空储蓄罐数量,和装满钱币的储蓄罐重量
s-=tmp; //计算钱币所占重量
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&list[i].v,&list[i].w);
}
for(int i=0;i<=s;i++){
dp[i]=INF;
}
dp[0]=0; //因为要求所有物品恰好装满,所以初始时,除dp[0]外,其余dp[j]均为无穷(或者不存在)
for(int i=1;i<=n;i++){
//遍历所有物品
for (int j=list[i].w;j<=s;j++) {
//完全背包,顺序遍历所有可能转移的状态
if (dp[j-list[i].w]!=INF) //若dp[j-list[i].w]不为无穷,就可以由此状态转移而来
dp[j]=min(dp[j],dp[j-list[i].w]+list[i].v); //取 转移值和原值的较小值
}
}
if (dp[s] != INF) //若存在一种方案使背包恰好装满,输出其最小值
printf("The minimum amount of money in the piggy-bank is %d.\n",dp[s]);
else //若不存在方案
puts("This is impossible.");
}
return 0;
}
总结一下完全背包问题,其特点为每个物品可选的数量为无穷,其解法与0-1背包整体保持一致,与其不同的仅为状态更新时的遍历顺序。时间复杂度和空间复杂度均和0-1背包保持一致。
最后,我们介绍多重背包问题,其介于0-1背包和完全背包之间:有容积为v的背包,给定一些物品,每种物品包含体积w、价值v、和数量k,求用该背包能装下的最大价值总量。
与之前的背包问题都不同,每种物品可选的数量不再为无穷或者1,而是介于其中的一个确定的数k。与之前讨论的问题一样,我们可以将多重背包问题直接转化到0-1背包上去,即每种物品均被视为k种不同物品,对所有的物品求0-1背包,其时间复杂度为:
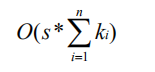
由此可见,降低每种物品的数量ki 将会大大的降低其复杂度,于是我们采用一种更为有技巧性的拆分。将原数量为k的物品拆分为若干组,每组物品看成一件物品,其价值和重量为该组中所有物品的价值重量总和,每组物品包含的原物品个数分别为:为: 1、 2、4…k-2c+1, 其中c为使k-2c+1大于0的最大整数。这种类似于二进制的拆分,不仅将物品数量大大降低,同时通过对这些若干个原物品组合得到新物品的不同组合,可以得到0到k之间的任意件物品的价值重量和,所以对所有这些新物品做0-1背包,即可得到多重背包的解。由于转化后的0-1背包物品数量大大降低,其时间复杂度也得到较大优化,为:
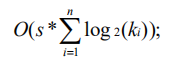
Problem 3


在该例中,对每个物品的总数量进行了限制,即多重背包问题。我们对每种物品进行拆分,使物品数量大大减少,同时通过拆分后的物品间的组合又可以组合出所有物品数量的情况。
#include <stdio.h>
struct E{
//大米
int w; //价格
int v; //重量
}list[2001];
int dp[101];
int max(int a,int b){
return a>b?a:b;}//取最大值函数
int main(){
int T;
scanf("%d",&T);
while (T --) {
int s,n;
scanf("%d%d",&s,&n);
int cnt=0; //拆分后物品总数
for(int i=1;i<=n;i++){
int v,w, k;
scanf("%d%d%d",&w,&v,&k);
int c=1;
while (k-c>0) {
//对输入的数字k,拆分成1,2, 4...k-2^c + 1,其中c为使最后一项大于0的最大整数
k-=c;
list[++cnt].w=c*w;
list[cnt].v=c*v; //拆分后的大米重量和价格均为组成该物品的大米的重量价格和
c*=2;
}
list[++cnt].w=w*k;
list[cnt].v=v*k;
}
for (int i=1;i <=s;i++) dp[i]=0; //初始值
for (int i=1;i <= cnt;i++) {
//对拆分后的所有物品进行0-1背包
for (int j=s;j >= list[i].w;j--) {
dp[j]=max(dp[j],dp[j -list[i].w] + list[i].v);
}
}
printf("%d\n",dp[s]);
}
return 0;
}
总结多重背包问题:多重背包的特征是每个物品可取的数量为一个确定的整数,我们通过对这个整数进行拆分,使若干个物品组合成一个价值和体积均为这几个物品的和的大物品,同时通过这些大物品的间的组合又可以组合出选择任意件物品所包含的体积和重量情况,通过这种拆分使最后进行0-1背包的物品数量大大减少,从而降低复杂度,其时间复杂的为:
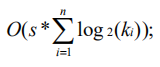
空间复杂度与0-1背包保持一致。