opencv学习17-19——laplacian滤波，Emboss滤波，Log滤波

Q17:laplacian滤波

laplacian 是边缘检测的一种，算子如下

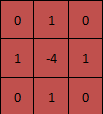
代码如下

#include"opencv2/core/core.hpp"
#include"opencv2/highgui/highgui.hpp"
#include<opencv2/opencv.hpp>
#include "math.h"
#include"iostream"
using namespace std;
using namespace cv;
#define Kernel_size 3
Mat laplacian3(Mat img){
	//构建3*3滤波系数矩阵
	double K[Kernel_size][Kernel_size] = {
   
   {0,1,0},{1,-4,1},{0,1,0}};  
	int imgrow = img.rows;
    int imgcol = img.cols;
	Mat out = Mat::zeros(imgrow,imgcol,CV_8UC1);
	int dot = floor((float)(Kernel_size/2));
	int v;
	for(int i=floor((float)(Kernel_size/2));i<imgrow-floor((float)(Kernel_size/2));i++){
		for(int j=floor((float)(Kernel_size/2));j<imgcol-floor((float)(Kernel_size/2));j++){
			v = 0;
			for(int i_=-dot;i_<dot+1;i_++){
				for(int j_=-dot;j_<dot+1;j_++){
						v += img.at<uchar>(i+i_,j+j_)*K[i_+dot][j_+dot];
				}
			}
			if(v>=0)
				out.at<uchar>(i,j) = v;
			else
				out.at<uchar>(i,j) = -v;
		}
	}
	return out;
}
void main(){
	Mat img = imread("ck567.jpg",IMREAD_GRAYSCALE);
	Mat out1 = laplacian3(img);
	imshow("laplacian3",out1);                                                                                                             
	imshow("original-pic",img);
	waitKey(0);
	destroyAllWindows();
}

效果如下

Q18:Emboss滤波

算子如下

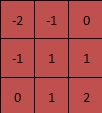
代码如下

#include"opencv2/core/core.hpp"
#include"opencv2/highgui/highgui.hpp"
#include<opencv2/opencv.hpp>
#include "math.h"
#include"iostream"
using namespace std;
using namespace cv;
#define Kernel_size 3
Mat emboss3(Mat img){
	//构建3*3滤波系数矩阵
	double K[Kernel_size][Kernel_size] = {
   
   {-2,-1,0},{-1,1,1},{0,1,2}};  
	int imgrow = img.rows;
    int imgcol = img.cols;
	Mat out = Mat::zeros(imgrow,imgcol,CV_8UC1);
	int dot = floor((float)(Kernel_size/2));
	int v;
	for(int i=floor((float)(Kernel_size/2));i<imgrow-floor((float)(Kernel_size/2));i++){
		for(int j=floor((float)(Kernel_size/2));j<imgcol-floor((float)(Kernel_size/2));j++){
			v = 0;
			for(int i_=-dot;i_<dot+1;i_++){
				for(int j_=-dot;j_<dot+1;j_++){
						v += img.at<uchar>(i+i_,j+j_)*K[i_+dot][j_+dot];
				}
			}
			if(v>=0)
				out.at<uchar>(i,j) = v;
			else
				out.at<uchar>(i,j) = -v;
		}
	}
	return out;
}
void main(){
	Mat img = imread("ck567.jpg",IMREAD_GRAYSCALE);
	Mat out1 = emboss3(img);
	imshow("emboss3",out1);                                                                                                             
	imshow("original-pic",img);
	waitKey(0);
	destroyAllWindows();
}

效果如下

 Q19:Log滤波

Log滤波又称为高斯-拉普拉斯滤波，先进行高斯平滑在进行拉氏滤波，其中高斯平滑的公式为log的定义式。

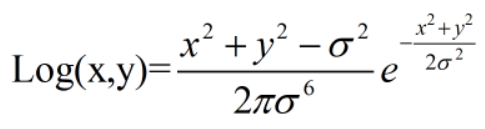
代码如下

#include"opencv2/core/core.hpp"
#include"opencv2/highgui/highgui.hpp"
#include<opencv2/opencv.hpp>
#include "math.h"
#include"iostream"
using namespace std;
using namespace cv;
#define M_PI 3.14159265358979323846
#define Kernel_size 5
#define sigma 3
Mat Log_filter(Mat img){
	//构建3*3滤波系数矩阵
	double K[Kernel_size][Kernel_size];  
	int imgrow = img.rows;
    int imgcol = img.cols;
	Mat out = Mat::zeros(imgrow,imgcol,CV_8UC1);
	int dot = floor((float)(Kernel_size/2));
	double Sum = 0;
	int x = 0;
	int y = 0;
	for(int i=0;i<Kernel_size;i++){
		for(int j=0;j<Kernel_size;j++){
			x = j-dot;
			y = i-dot;
			K[i][j] = (x*x+y*y-sigma*sigma)/(2*M_PI*pow((double)sigma,6))*exp((-(x*x+y*y)/(2*sigma*sigma))*1.0);
			Sum += K[i][j];
		}
	}
	for(int i=0;i<Kernel_size;i++){
		for(int j=0;j<Kernel_size;j++){
			K[i][j] /= Sum;
		}
	}
	int v;
	for(int i=floor((float)(Kernel_size/2));i<imgrow-floor((float)(Kernel_size/2));i++){
		for(int j=floor((float)(Kernel_size/2));j<imgcol-floor((float)(Kernel_size/2));j++){
			v = 0;
			for(int i_=-dot;i_<dot+1;i_++){
				for(int j_=-dot;j_<dot+1;j_++){
						v += img.at<uchar>(i+i_,j+j_)*K[i_+dot][j_+dot];
				}
			}
			if(v>=0)
				out.at<uchar>(i,j) = v;
			else
				out.at<uchar>(i,j) = -v;
		}
	}
	return out;
}
void main(){
	Mat img = imread("ck567.jpg",IMREAD_GRAYSCALE);
	Mat out1 = Log_filter(img);
	imshow("Log_filter",out1);                                                                                                             
	imshow("original-pic",img);
	waitKey(0);
	destroyAllWindows();
}

 效果如下