区间分组
给定N个闭区间[ai,bi],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
输入格式
第一行包含整数N,表示区间数。
接下来N行,每行包含两个整数ai,bi,表示一个区间的两个端点。
输出格式
输出一个整数,表示最小组数。
数据范围
1≤N≤10^5,
−109≤ai≤bi≤109
输入样例:
3
-1 1
2 4
3 5
输出样例:
2
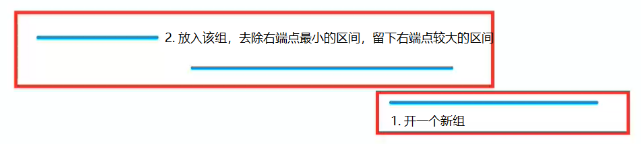
思路:贪心,先将区间按左端点排序,因为要组数尽量小,所以枚举时,和每一个组的最后一个区间比较,只要大于最后一个区间的右端点,说明无重合,将本区间放入当前组;否则,看下一组。这样的时间复杂度是O(n ^ 2)。明显时间上不满足要求。可以优化的地方是对n个组的遍历。我们可以用树来存储。用单调队列存储右端点的值。这样遍历就由O(n) -> O(logN),时间上就满足条件了。
代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
int n;
bool cmp(pair<int, int> a, pair<int, int> b)
{
return a.x < b.x;
}
priority_queue<int, vector<int>, greater<int>> heap;
PII q[100010];
int main(){
cin >> n;
for(int i = 0; i < n; i++ )
{
int a, b;
cin >> a >> b;
q[i] = {
a, b};
}
sort(q, q + n, cmp);
for(int i = 0; i < n; i++){
//这个地方需要用堆来处理一下,进行优化
if(heap.empty() || heap.top() >= q[i].x){
heap.push(q[i].y);
}
else heap.pop(),heap.push(q[i].y);
}
cout << heap.size();
return 0;
}