空间域滤波
(1)基础
i.机理
空间滤波器由(1)一个邻域(图像中的一个较小的矩阵),(2)对该邻域的图像像素执行预定义操作(线性、非线性)组成。滤波器的中心访问图像中的每个像素,就产生了滤波后的图像。如果滤波是线性操作,则滤波器就是线性空间滤波器。如果滤波是非线性操作,那么滤波器就是非线性滤波器。空间滤波大多数使用空间滤波器直接作用于图像本身像素完成图像平滑等操作。线性空间滤波器于频率域滤波器之间存在一一对应的关系。然而,空间滤波可提供相当多的功能,同时还可用于非线性滤波,这在频率域是做不到的。空间滤波器的机理,滤波后的g(x,y)如下所示。

g(x,y)扩展后的公式如下所示:
![]()
为了更立体显示的话,如下图所示。

上述操作是相关操作,另一个是卷积操作,卷积首先要旋转180度,然后进行相关操作。
(2)平滑空间滤波器
i.平滑线性过滤器(均值过滤器)
均值过滤器是指包含在滤波器模板邻域内像素总和的平均值。典型的随机噪声是由灰度级的急剧变化组成,因此,均值过滤器用于模糊处理和降低噪声。同时图像边缘也是由图像灰度尖锐变化带来的特征,均值滤波还是存在边缘模糊的负面效应。

均值过滤器是将图像模糊化,原理是利用像素均值来模糊整个图像。而均值过滤器的模板大小设定则是由融入背景物体尺寸来决定的。
上图中的第二个图时加权平均过滤器,加权平均考虑了像素之间的重要性,相比均值过滤器更重要一些。
ii.统计排序(非线性)滤波器
统计排序滤波器以统计排序的值代替中心像素的值。如,中值、最大值及最小值滤波器。它的主要功能是使拥有不同灰度的点看起来更接近于它的相邻点,具有非常优秀的去噪能力,而且比相同尺寸的线性平滑滤波的模糊程度明显要低。
均值滤波用邻域内像素的平均值来代替中心像素的值,相当于低通滤波,有将图像模糊化的趋势,对椒盐噪声基本无能为力。
中值滤波是将像素邻域内灰度的中值来代替中心像素的值,把不同灰度的像素点看起来更接近于邻域内的像素点,优点是可以很好的过滤掉椒盐噪声,缺点是易造成图像的不连续性。
最大值滤波是用邻域内像素的最大值来代替中心像素的值,对图像中的最亮点非常有用,并消除图像中的“椒”噪声(亮度值小的噪声)。
最小值滤波是用邻域内像素的最小值来代替中心像素的值,对图像中的最暗点非常有用,并消除图像中的“盐”噪声(亮度值大的噪声)。
阿尔法均值过滤器是在邻域内去掉最低灰度值的d/2和最高值的d/2,利用剩下的mn-d个像素的平均值来代替中心像素的值,对高斯噪声和椒盐噪声混合有很好作用。d等于0的情况下,改滤波器退化成均值滤波器。
iii.自适应滤波器
上述滤波器并没有考虑图像中的一点对于其他点的特征变化,自适应滤波器的特性变化是以mxn的矩阵窗口Sxy定义的滤波器区域内图像的统计特性为基础的,自适应滤波器相比上述2个滤波器具有很好的性能。同时也增加了滤波器的复杂度。自适应滤波器所达到的效果与算术和几何均值滤波器相似,重要的是图像更清晰一些(数字图像处理图5.13结论)。
自适应滤波器是建立在均值和方差基础上的,均值给出了邻域内平均灰度的度量,而方差(每个像素点的灰度值减去图像平均灰度值的平方和除以总的像素个数)则给出了邻域内对比度的度量。
自适应中值滤波器可以更好的处理具有更大概率的脉冲噪声,另一个优点是平滑非脉冲噪声时试图保留细节,这是传统中值滤波器所做不到的。
其他常见自适应过滤器,如LMS、NLMS、RLS
(3)锐化空间滤波器
锐化处理的主要目的是为了突出图像上地物的边缘、轮廓,或某些线性目标要素的特征。这种滤波方法提高了地物边缘与周围像元之间的反差,因此也被称为边缘增强。主要是用到微分来定义和实现锐化算子方法。微分算子的响应强度与图像在用算子操作的这一点的突变程度成正比,这样微分算子增强边缘和其他突变(噪声),削弱灰度变化缓慢的区域。
我们最感兴趣的是恒定灰度区域中,突变的开始点与结束点(台阶和斜坡突变)及沿着灰度斜坡处的微分性质。这些类型的突变可以用来对图像中的噪声点、线与边缘建模。
一阶微分算子必须保证以下几点:(1)在恒定灰度区域的微分值为0;(2)在灰度台阶或斜坡处微分值非0;(3)沿着斜坡的微分值非0
二阶微分算子必须保证以下几点:(1)在恒定区域的微分值为0;(2)在灰度台阶或斜坡的起点处微分值非0;(3)沿着斜坡的微分值非0

数字图像中的边缘在灰度上常常类似于斜坡过度,这样就导致图像的一阶微分产生较粗的边缘,因为沿着斜坡的微分非零。另一方面,二阶微分产生由零分开的一个像素宽的双边缘。二阶微分在增强细节方面要比一阶微分好得多,这是一个适合锐化图像的理想特性。首先介绍一下一维函数f(x),其一阶微分的基本定义时差值:
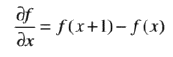
二阶微分和图像一阶微分保持一致,具体差值我微分方程如下:

i.拉普拉斯算子
拉普拉斯算子就是二维函数的二阶微分的离散公式,然后构造一个基于该公式的滤波器模板组成的。最关注的是一种各向同性滤波器,这种滤波器的响应与滤波器作用的图像的突变方向无关。各向同性滤波器是旋转不变的,即将源图像选择后进行滤波处理给出的结果与先对图像滤波然后再选择的结果相同。一个二维图像函数f(x,y)的拉普拉斯算子定义为:
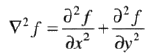
离散描述上述公式,在x、y方面拉布拉斯公式如下:
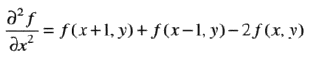
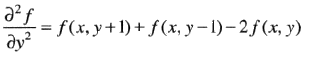
合并后的结果如下:
![]()
拉布拉斯在图像细节的增强方面有一定的优点,在增强细节方面它是最好的。同时会导致产生比梯度操作更多的噪声。
(4)微分过滤器
后续补充
(5)混合空间增强法
数字图像处理例子https://blog.csdn.net/xiaosha00000/article/details/84861893
利用各个过滤器的特征进行融合使用,可达到最佳效果。例子稍后进行实验
(5)模糊集合
模糊集合在解决那些不以精确概率为基础来表述的问题时,为体现人类知识提供一个框架。