算法打卡（六）-----根节点到叶子节点之和

力扣：112

问题描述：

给你二叉树的根节点root和一个表示目标的整数targetSum，判断该树中是否存在根节点到叶子节点之和等于目标值。

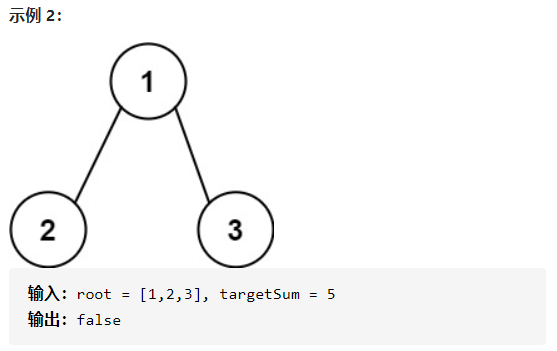
问题分析：

其实这道题就是一道广度优先遍历的题，遍历所有的叶子节点到根节点的路径之和再与目标值进行比对，如果相等则返回true，否则返回false。

这里我们以这个二叉树来进行具体分析。

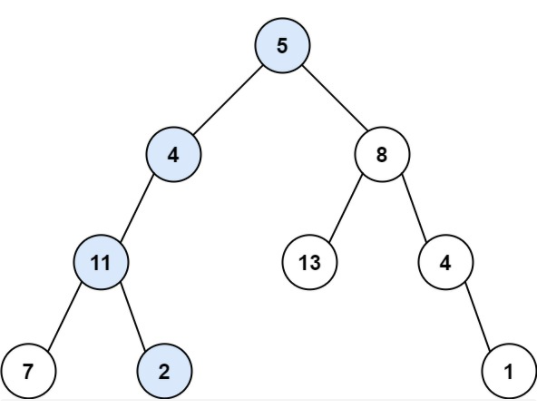
我们求一条根节点到叶子节点和为22的路径，判断该二叉树是否存在这样的路径。

算法分析：

• 我们需要创建两个队列，一个用于保存我们即将要遍历的节点，另一个保存我们遍历到该节点的路径之和。

//这个队列是用于存放即将要遍历的结点
Queue<TreeNode> queNode=new LinkedList<>();
//这个队列是用于存放根节点到当前节点的路径之和
Queue<Integer> queVal=new LinkedList<>();

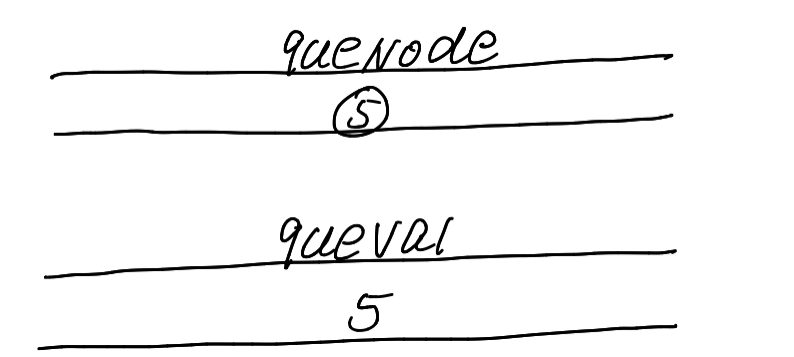
• 然后我们依次进行遍历每一层节点，直到叶子节点

• 当遍历到叶子节点与目标值进行比较，是否相同。

递归方法计算

这道题还可以用递归方法来进行求解。使用递归我们就要从方法的参数上来进行考虑。当我们使用递归的时候就需要和广度优先遍历的思想相反，我们在广度优先遍历的时候是逐渐向目标值靠近，而我们使用递归的时候是相反，逐渐向节点数据值靠近。

public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }