欧式距离
欧式距离也称为欧几里得距离或者欧几里得度量,是一个通常采用的距离定义,它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧式距离就是两点之间的距离。
二维:
x = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} (x2−x1)2+(y2−y1)2
( x 2 , y 2 ) (x_2,y_2) (x2,y2)到原点的欧式距离为:|x| = x 2 2 + y 2 2 \sqrt{x_2^2+y_2^2} x22+y22
三维:
x = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 1 − z 2 ) 2 \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_1 - z_2)^2} (x2−x1)2+(y2−y1)2+(z1−z2)2
( x 2 , y 2 , z 2 ) (x_2,y_2, z_2) (x2,y2,z2)到原点的欧式距离为:|x| = x 2 2 + y 2 2 + z 2 2 \sqrt{x_2^2+y_2^2+z_2^2} x22+y22+z22
曼哈顿距离
曼哈顿距离也称为出租车几何,用来标明两个点在标准坐标系上的绝对坐标轴距离和。

在图2中,假设从B1到达C3,则曼哈顿距离可以表示为
x = ( 3 − 2 ) + ( 3 − 1 ) = 3 x = (3-2)+(3 - 1)= 3 x=(3−2)+(3−1)=3
欧式距离与曼哈顿距离的比较
下面我们通过一张经典的示例来说明两者的区别。
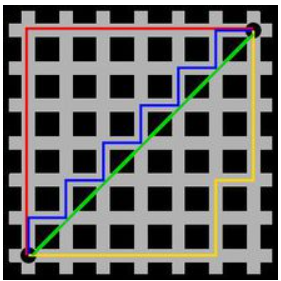
(为了方便说明,我们假设左下角的起点为A,右上角的终点为B)从图中可以看出,绿色的线表示为欧式距离,而红色的 线为曼哈顿距离,其他的蓝色的线和黄色的线都可以表示为曼哈顿距离的变形。
再来看图2,其实,我们也可以算出它的欧式距离(还是相同的题目)
x = ( 3 − 2 ) 2 + ( 3 − 1 ) 2 = 5 x = \sqrt{(3 - 2)^2+(3 - 1)^2} = \sqrt{5} x=(3−2)2+(3−1)2=5
余弦距离
余弦距离,也称为余弦相似度,是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
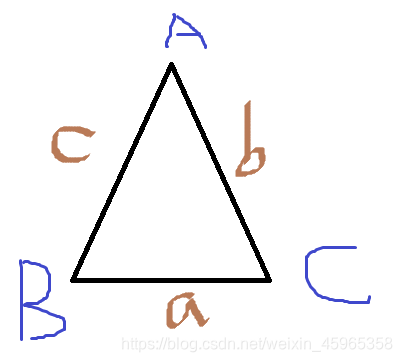
角A的余弦为: c o s A = b 2 + c 2 − a 2 2 b c cos A =\frac {b^2+c^2 -a^2}{2bc} cosA=2bcb2+c2−a2
汉明距离
在信息论中,两个等长字符串之间的汉明距离(英语:Hamming distance)是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
例如:
- 1011101与1001001之间的汉明距离是2。
- 2143896与2233796之间的汉明距离是3。
- "toned"与"roses"之间的汉明距离是3。
-