一、简介
BP网络(Back Propagation),是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。
在人工神经网络发展历史中,很长一段时间里没有找到隐层的连接权值调整问题的有效算法。直到误差反向传播算法(BP算法)的提出,成功地解决了求解非线性连续函数的多层前馈神经网络权重调整问题。
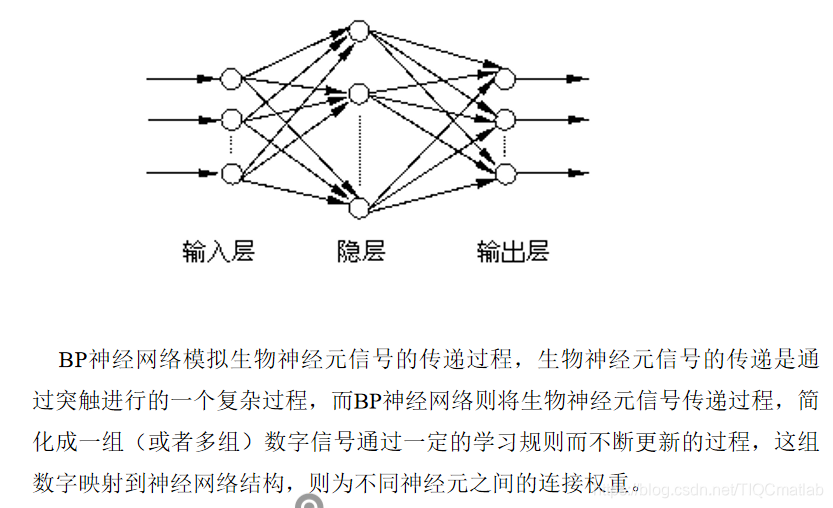
BP (Back Propagation)神经网络,即误差反传误差反向传播算法的学习过程,由信息的正向传播和误差的反向传播两个过程组成。输入层各神经元负责接收来自外界的输入信息,并传递给中间层各神经元;中间层是内部信息处理层,负责信息变换,根据信息变化能力的需求,中间层可以设计为单隐层或者多隐层结构;最后一个隐层传递到输出层各神经元的信息,经进一步处理后,完成一次学习的正向传播处理过程,由输出层向外界输出信息处理结果。当实际输出与期望输出不符时,进入误差的反向传播阶段。误差通过输出层,按误差梯度下降的方式修正各层权值,向隐层、输入层逐层反传。周而复始的信息正向传播和误差反向传播过程,是各层权值不断调整的过程,也是神经网络学习训练的过程,此过程一直进行到网络输出的误差减少到可以接受的程度,或者预先设定的学习次数为止。
BP神经网络模型BP网络模型包括其输入输出模型、作用函数模型、误差计算模型和自学习模型。


2 BP神经网络模型及其基本原理
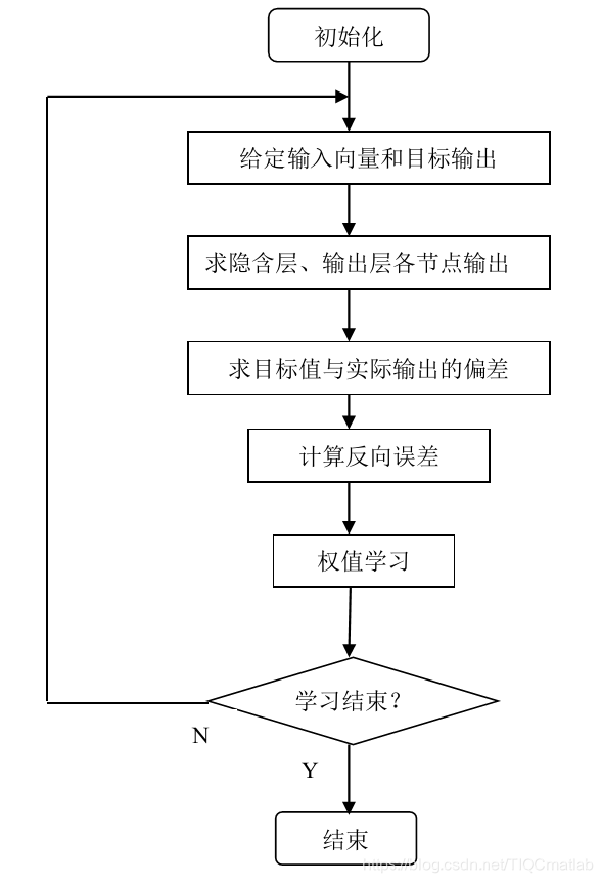
3 BP_PID算法流程
二、源代码
%BP based PID Control
clc,clear,close all
warning off
xite=0.25; % 学习因子
alfa=0.05; % 惯量因子
S=1; %Signal type
%NN Structure
IN=4; % 输入层个数
H=5; % 隐藏层个数
Out=3; % 输出层个数
if S==1 %Step Signal
wi=[-0.6394 -0.2696 -0.3756 -0.7023;
-0.8603 -0.2013 -0.5024 -0.2596;
-1.0749 0.5543 -1.6820 -0.5437;
-0.3625 -0.0724 -0.6463 -0.2859;
0.1425 0.0279 -0.5406 -0.7660];
%wi=0.50*rands(H,IN);
wi_1=wi;wi_2=wi;wi_3=wi;
wo=[0.7576 0.2616 0.5820 -0.1416 -0.1325;
-0.1146 0.2949 0.8352 0.2205 0.4508;
0.7201 0.4566 0.7672 0.4962 0.3632];
%wo=0.50*rands(Out,H);
wo_1=wo;wo_2=wo;wo_3=wo;
end
if S==2 %Sine Signal
wi=[-0.2846 0.2193 -0.5097 -1.0668;
-0.7484 -0.1210 -0.4708 0.0988;
-0.7176 0.8297 -1.6000 0.2049;
-0.0858 0.1925 -0.6346 0.0347;
0.4358 0.2369 -0.4564 -0.1324];
%wi=0.50*rands(H,IN);
wi_1=wi;wi_2=wi;wi_3=wi;
wo=[1.0438 0.5478 0.8682 0.1446 0.1537;
0.1716 0.5811 1.1214 0.5067 0.7370;
1.0063 0.7428 1.0534 0.7824 0.6494];
%wo=0.50*rands(Out,H);
wo_1=wo;wo_2=wo;wo_3=wo;
end
x=[0,0,0];
u_1=0;u_2=0;u_3=0;u_4=0;u_5=0;
y_1=0;y_2=0;y_3=0;
% 初始化
Oh=zeros(H,1); %从隐藏层到输出层
I=Oh; %从输入层到隐藏层
error_2=0;
error_1=0;
ts=0.001;
for k=1:1:500
time(k)=k*ts;
if S==1
rin(k)=1.0;
elseif S==2
rin(k)=sin(1*2*pi*k*ts);
end
%非线性模型
a(k)=1.2*(1-0.8*exp(-0.1*k));
yout(k)=a(k)*y_1/(1+y_1^2)+u_1; % 输出
error(k)=rin(k)-yout(k); % 误差
xi=[rin(k),yout(k),error(k),1];
x(1)=error(k)-error_1;
x(2)=error(k);
x(3)=error(k)-2*error_1+error_2;
epid=[x(1);x(2);x(3)];
I=xi*wi';
for j=1:1:H
Oh(j)=(exp(I(j))-exp(-I(j)))/(exp(I(j))+exp(-I(j))); %Middle Layer
end
K=wo*Oh; %Output Layer
for l=1:1:Out
K(l)=exp(K(l))/(exp(K(l))+exp(-K(l))); %Getting kp,ki,kd
end
kp(k)=K(1);ki(k)=K(2);kd(k)=K(3);
Kpid=[kp(k),ki(k),kd(k)];
du(k)=Kpid*epid;
u(k)=u_1+du(k);
% 饱和限制
if u(k)>=10
u(k)=10;
end
if u(k)<=-10
u(k)=-10;
end
dyu(k)=sign((yout(k)-y_1)/(u(k)-u_1+0.0000001));
%Output layer
for j=1:1:Out
dK(j)=2/(exp(K(j))+exp(-K(j)))^2;
end
for l=1:1:Out
delta3(l)=error(k)*dyu(k)*epid(l)*dK(l);
end
三、运行结果




四、备注
完整代码或者代写添加QQ912100926
往期回顾>>>>>>
【预测模型】粒子群之lssvm预测模型【Matlab 005期】
【lssvm预测】鲸鱼优化算法之lssvm预测【Matlab 006期】
【SVM预测】蝙蝠算法之SVM预测模型【Matlab 007期】
【SVM预测】灰狼算法优化之SVM支持向量机预测模型【Matlab 008期】
【预测模型】基于BP神经网络的预测模型【Matlab 009期】
【lssvm预测】蝙蝠算法之改进的最小二乘支持向量机lssvm预测【Matlab 010期】
【ISTM预测】鲸鱼优化算法之改进的lSTM预测【Matlab 045期】
【SVM预测】蝙蝠算法之改进SVM预测模型【Matlab 046期】
【lSSVM预测】鲸鱼优化算法之lSSVM数据预测【Matlab 140期】
【ANN预测模型】差分算法之改进ANN网络预测【Matlab 141期】
【预测模型】RBF神经网络预测模型【Matlab 142期】
【预测模型】SVM回归预测算法之预测股票趋势【Matlab 143期】