网络参数
这里仅引入网络的一些参数的定义、说明和计算
(1)点度
- 网络中节点 U i U_i Ui 的度 k i k_i ki :与节点 i i i 连接的边数。
- 网路的平均度< k k k>:所有节点 U i U_i Ui 的度 k i k_i ki 的平均值。 < k > = 1 N ∑ i = 1 N k i <k>=\frac{1}{N}\sum_{i=1}^Nk_i <k>=N1i=1∑Nki
- 点度的求解:
- 构造邻接矩阵(由 0 , 1 0,1 0,1构成的) A = [ a 11 a 12 ⋯ a 1 N a 21 a 22 ⋯ a 2 N ⋮ ⋮ ⋱ ⋮ a N 1 a N 2 ⋯ a N N ] A=\left[ \begin{matrix} a_{11} & a_{12} & \dotsb & a_{1N}\\ a_{21} & a_{22} & \dotsb & a_{2N}\\ \vdots & \vdots & \ddots & \vdots\\ a_{N1} & a_{N2} & \dotsb & a_{NN} \end{matrix} \right] A=⎣⎢⎢⎢⎡a11a21⋮aN1a12a22⋮aN2⋯⋯⋱⋯a1Na2N⋮aNN⎦⎥⎥⎥⎤
- A 2 A^2 A2的对角元素 a i i ( 2 ) a_{ii}^{(2)} aii(2) 就是 k i k_i ki。
- 平均度的求解
- 根据上面的结果 < k > = t r ( A 2 ) N ( t r 代 表 矩 阵 的 迹 ) <k>=\frac{tr(A^2)}{N}~~~(tr代表矩阵的迹) <k>=Ntr(A2) (tr代表矩阵的迹)
(2)路径
- 距离:网络中两个节点 ( v i , v j ) (v_i,v_j) (vi,vj)的距离 d i j d_{ij} dij定义为连接这两个节点的最短路径上的边数。
- 效率:网络中两个节点 ( v i , v j ) (v_i,v_j) (vi,vj)间的效率为 1 d i j \displaystyle\frac{1}{d_{ij}} dij1,这个参量用来度量节点间信息传递速度。
- 网络的直径 D D D:任意两个节点的距离的最大值。 D = max 1 ≤ i < j ≤ N d i j D=\max_{1\le i<j\le N}d_{ij} D=1≤i<j≤Nmaxdij
- 网络的平均路径长度 L L L:任意两个节点的距离的平均值。(注意这里假定是一个连通的图) L = 1 C N 2 ∑ 1 ≤ i < j ≤ N d i j L=\frac{1}{C_N^2}\sum_{1\le i<j\le N}d_{ij} L=CN211≤i<j≤N∑dij
其中 C N 2 C_N^2 CN2 代表存在的距离的数量,从 N N N 中任意选取两个点。 - 求解参数的步骤:
- 构造图的邻接矩阵。
- 应用Floyd算法求出任意节点间的距离。
- 通过上面的定义可以求出网络直径 D D D 和 网络平均距离 L L L。
(3)聚类系数
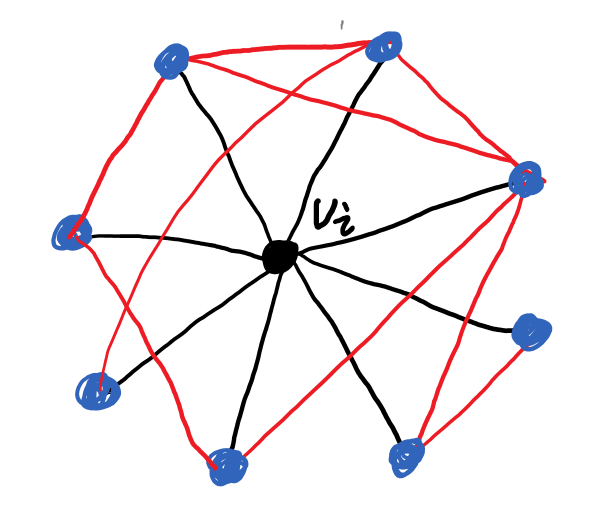
- 节点 v i v_i vi 的聚类系数
c i = k i 个 邻 接 点 之 间 存 在 的 边 数 E i k i 个 邻 接 点 之 间 可 能 存 在 的 最 大 边 数 = E i C k i 2 = 与 v i 相 连 的 三 角 形 的 数 量 n 1 与 v i 相 连 的 三 元 组 的 数 量 n 2 \begin{aligned} c_i &= \frac{k_i个邻接点之间存在的边数E_i}{k_i个邻接点之间可能存在的最大边数}\\ &= \frac{E_i}{C_{k_i}^2}\\ &= \frac{与v_i相连的三角形的数量n_1}{与v_i相连的三元组的数量n_2} \end{aligned} ci=ki个邻接点之间可能存在的最大边数ki个邻接点之间存在的边数Ei=Cki2Ei=与vi相连的三元组的数量n2与vi相连的三角形的数量n1
-
整个网络的聚类系数 c = 1 N ∑ i = 1 N c i c=\frac{1}{N}\sum_{i=1}^Nc_i c=N1i=1∑Nci明显有 0 ≤ c ≤ 1 0\le c\le 1 0≤c≤1,并且当 c = 0 c=0 c=0 时网络中任何两点之间无边, c = 1 c=1 c=1 时网络中任何两点之间有边。换句话说,当c离1越近说明网络联系越紧密,否则联系越松。
-
求解参数的步骤:
- 构造图的邻接矩阵 A A A。
- 求 A 2 A^2 A2 和 A 3 A^3 A3 ,其中各自的对角元素 a i i ( 2 ) a_{ii}^{(2)} aii(2)代表 k i k_i ki, a i i ( 3 ) a_{ii}^{(3)} aii(3)代表三角形的个数的两倍。
- 因此
c i = n 1 n 2 = 2 n 1 2 n 2 = 2 n 1 2 C k i 2 = a i i ( 3 ) a i i ( 2 ) ( a i i ( 2 ) − 1 ) c_i = \frac{n_1}{n_2}= \frac{2n_1}{2n_2}= \frac{2n_1}{2C_{k_i}^2}=\frac{a_{ii}^{(3)}}{a_{ii}^{(2)}(a_{ii}^{(2)}-1)} ci=n2n1=2n22n1=2Cki22n1=aii(2)(aii(2)−1)aii(3)
(4)点介数
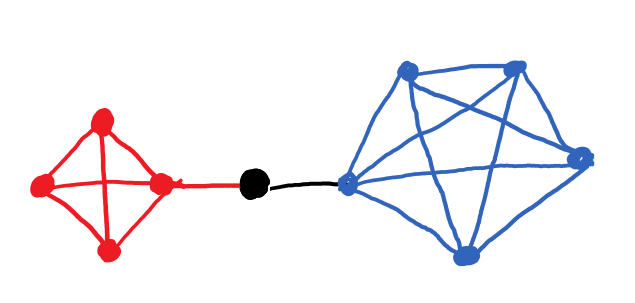
- 用来反映节点在整个网络中的作用和影响力,核心的想法设计如果某个节点 v i v_i vi 被其他许多最短路径经过,则表示该节点在网络中很重要。
- 参数表达式: B i = ∑ 1 ≤ j < l ≤ N j ≠ i ≠ l n j l ( i ) n j i B_i=\sum_{1\le j<l\le N j\not ={i\not ={l}}}\frac{n_{jl}(i)}{n_{ji}} Bi=1≤j<l≤Nj=i=l∑njinjl(i)
- n j i n_{ji} nji 表示 v j v_j vj 和 v l v_l vl 之间的最短路径的条数,就是说有多少路径长度都是最短的。
- n j l ( i ) n_{jl}(i) njl(i) 表示 v j v_j vj 和 v l v_l vl 之间最短路径经过 v i v_i vi 的条数。
(5)紧密度
- 紧密度测量了节点 v i v_i vi 通过最短路径与其它节点的接近程度 c i c = 1 L i = n − 1 ∑ j ∈ τ , j ≠ i d i j c_i^c=\frac{1}{L_i}=\frac{n-1}{\displaystyle\sum_{j\in\tau,j\not ={i}}d_{ij}} cic=Li1=j∈τ,j=i∑dijn−1
- τ \tau τ:节点 v i v_i vi 所能到达的节点的集合。
- n n n:表示 τ \tau τ 中含有的全部的点的个数。
- L i L_i Li:节点 v i v_i vi 到其它所有能够到达节点的平均距离。
- 紧密度指标用于刻画网络中的节点通过网络到达网络中其他节点的难易程度。反映的是节点通过网络对其他节点的施加影响的能力。
(6)特征向量中心性
- 给定一个网络,指派给网络中的每个节点一个相对得分。对某个节点分值的贡献中连到高分值节点的连接比连到低分值节点的连接多。
- 对于节点 v i v_i vi,记 x i = 1 λ ∑ j = 1 N a i j x j x_i=\frac{1}{\lambda}\sum_{j=1}^Na_{ij}x_j xi=λ1j=1∑Naijxj
- 其中 N N N为节点总数, λ \lambda λ为常数, A A A 为邻接矩阵。
- 由上面可以推知 A x = λ x A\bold{x}=\lambda \bold{x} Ax=λx。
- 因此 x \bold{x} x 就是 A A A 的特征向量,根据Peron-Frobenius定理选取最大特征值对应的特征向量,对 x \bold{x} x做一个归一化处理之后特征向量对应位置的参数代表得分。