数学建模与数据分析中的典型相关分析

典型相关分析
之前的Spearman与Person相关系数分析都是分析两个变量，而典型相关分析就是在分析两组相关变量。
可以参考的文章：知乎SPSSAU
对下面的两组数据(三个生理指标和三个训练指标)

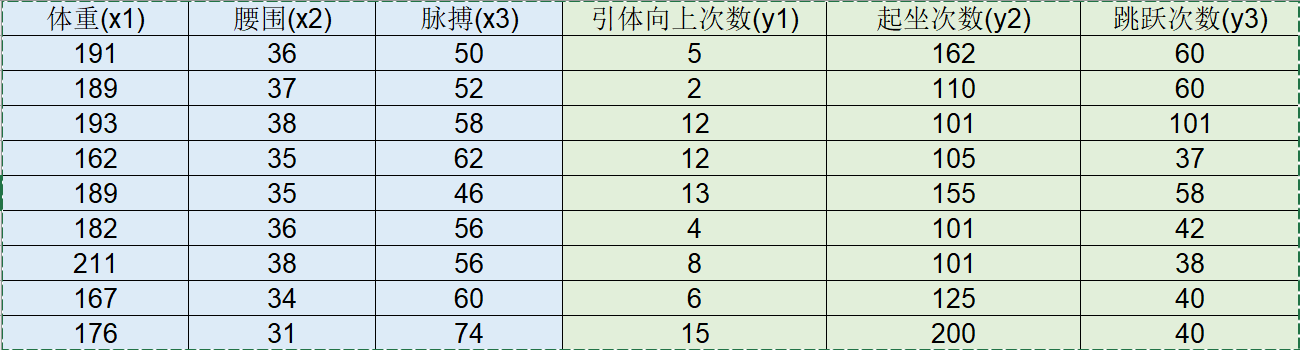
(1)典型相关分析

1.总体思想

• 将两组变量之间的相关性分析转化为一组变量的线性组合与另一组变量的线性组合之间的相关关系的分析。
• 首先：在两组变量内部各找一个线性组合，保证两个线性组合之间的相关系数最大。
• 然后：选取与之前选取的线性组合不相关的新的线性组合，同时也保证新选出的两个线性组合之间的相关系数最大。
• 一直取下去，直到所有相关性的信息被提取完毕。
• 选出的线性组合配对称为典型变量，相关系数称为典型相关系数。

2.原理分析

$①$ 假设有两个相互关联的随机向量 $$X^{(1)}=(X_1^{(1)},X_2^{(1)},\dots ,X_p^{(1)}),X^{(2)}=(X_1^{(2)},X_2^{(2)},\dots ,X_q^{(2)})。$$各选取原变量的线性组合 $U_i$ 和 $V_i$，使 $$U_i=a_1^{(i)}{X}_1^{(1)}+a_2^{(i)}{X}_2^{(1)}+\cdots +a_p^{(i)}{X}_p^{(1)}\stackrel{\Delta }{=}{a}^{(i{)}^{\prime }}{X}^{(1)}$$$$V_i=b_1^{(i)}{X}_1^{(2)}+b_2^{(i)}{X}_2^{(2)}+\cdots +b_p^{(i)}{X}_p^{(2)}\stackrel{\Delta }{=}{b}^{(i{)}^{\prime }}{X}^{(2)}$$这里的$i$表示第$i$组组合
$②$ 下面要求解保证 $a^{(i{)}^{\prime }}{X}^{(1)}$与 $b^{(i{)}^{\prime }}{X}^{(2)}$ 的相关系数最大的一组 $a^{(i{)}^{\prime }}，b^{(i{)}^{\prime }}$。例如：对 $i=1$ 在 $D(a^{(1{)}^{\prime }}{X}^{(1)})=1$ 和 $D(b^{(1{)}^{\prime }}{X}^{(2)})=1$ 的前提下(这个前提是为保证结果的唯一性)，求使 $\rho (a^{(1{)}^{\prime }}{X}^{(1)},b^{(1{)}^{\prime }}{X}^{(2)})$ 最大的 $a^{(1{)}^{\prime }}，b^{(1{)}^{\prime }}$。称 $a^{(1{)}^{\prime }}{X}^{(1)},b^{(1{)}^{\prime }}{X}^{(2)}$ 为 $X^{(1)},X^{(2)}$ 的第一对典型相关变量，以此类推可以求出第二对，第三对等。
$③$ 引入下面的记号 $$Cov(X^{(1)})=\sum _{11},Cov(X^{(2)})=\sum _{22}$$$$Cov(X^{(1)},X^{(2)})=\sum _{12}={\sum _{21}}^{\prime }$$
$④$ 给出下面的公式：$X$ 是一个 $n$ 维随机变量，$X_i(i=1,\cdots ,n)$ 均为随机变量。
$$X=\left[\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_n\end{array}\right]$$
$$E(X)=\left[\begin{array}{c}E(X_1)\\ E(X_2)\\ ⋮\\ E(X_n)\end{array}\right]$$
$$D(X)=E[(X-E(X))(X-E(X){)}^T]$$
对于一个列常数向量 $a$
$$D(a^{T}X)=a^{T}D(X)a$$
$$D(X)=Cov(X,X)$$
$$Cov(X,Y)=E[(X-E(X))(Y-E(Y){)}^T]$$
对于列常数向量 $a$ 与 $b$
$$Cov(aX,bY)=aE[(X-E(X))(Y-E(Y){)}^T]b^T$$
$⑤$ 代入上面的$U_i$与$V_i$
$$D(U_i)=D({a^{(i)}}^{\prime }{X}^{(1)})={a^{(i)}}^{\prime }\sum _{11}{a}^{(i)}$$
$$D(V_i)=D({b^{(i)}}^{\prime }{X}^{(2)})={b^{(i)}}^{\prime }\sum _{22}{b}^{(i)}$$
$$Cov(U_i,V_i)=Cov({a^{(i)}}^{\prime }{X}^{(1)},{b^{(i)}}^{\prime }{X}^{(2)})={a^{(i)}}^{\prime }\sum _{12}{b}^{(i)}$$
$$Corr(U_i,V_i)=\frac{Cov(U_i,V_i)}{\sqrt{D(U_i)}\sqrt{D(V_i)}}={a^{(i)}}^{\prime }\sum _{12}{b}^{(i)}$$ 由于已经认为 $D(a^{(i{)}^{\prime }}{X}^{(1)})=1$ 和 $D(b^{(i{)}^{\prime }}{X}^{(2)})=1$

$⑥$ 使用Lagrange乘数求 $Corr(U_i,V_i)$ 的最大值
$$\phi (a^{(i)},b^{(i)})={a^{(i)}}^{\prime }\sum _{12}{b}^{(i)}-\frac{\lambda }{2}(a^{(i{)}^{\prime }}{X}^{(1)}-1)-\frac{\gamma }{2}(b^{(i{)}^{\prime }}{X}^{(2)}-1)$$
$⑦$ 求出来的结果
$$\{\begin{array}{r}({\sum _{11}}^{-1}\sum _{12}{\sum _{22}}^{-1}\sum _{21}-{\lambda }^2{I}_q)a^{(i)}=0\\ ({\sum _{22}}^{-1}\sum _{21}{\sum _{11}}^{-1}\sum _{12}-{\lambda }^2{I}_p)b^{(i)}=0\end{array}$$
其中$I_p,I_q$表示 $p\times p,q\times q$ 阶的单位矩阵。
并且有$$\lambda ={a^{(i)}}^{\prime }\sum _{12}{b}^{(i)}=Corr(U_i,V_i)$$
$⑧$ 问题转化
令
$$A={\sum _{11}}^{-1}\sum _{12}{\sum _{22}}^{-1}\sum _{21}$$
$$B={\sum _{22}}^{-1}\sum _{21}{\sum _{11}}^{-1}\sum _{12}$$
则求 $Corr(U_i,V_i)$ 的最大值也就是求 $\lambda$ 的最大值，而求 $\lambda$ 的最大值，可以将 $⑦$ 中的两个式子看成$(A-\lambda I)x=0$,进而就可以转化成为求解最大特征值，同时对应的$a^{(1)},b^{(1)}$ 也就是最大特征向量。

3.步骤的简单说明

• 求解典型变量和典型相关系数$$U_i=a_1^{(i)}{X}_1^{(1)}+a_2^{(i)}{X}_2^{(1)}+\cdots +a_p^{(i)}{X}_p^{(1)}\stackrel{\Delta }{=}{a}^{(i{)}^{\prime }}{X}^{(1)}$$$$V_i=b_1^{(i)}{X}_1^{(2)}+b_2^{(i)}{X}_2^{(2)}+\cdots +b_p^{(i)}{X}_p^{(2)}\stackrel{\Delta }{=}{b}^{(i{)}^{\prime }}{X}^{(2)}$$
• 对典型相关系数 ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_s$ 进行假设检验。
  • 具体检验的方法
    $H_0:{\lambda }_{k+1}={\lambda }_{k+2}=\cdots ={\lambda }_r=0$
    $H_1:{\lambda }_{k+1}\ne 0$
    其中 $k=0,1,\cdots$
    当检验 ${\lambda }_1\ne 0$ 之后再检验 ${\lambda }_2$ 是否 $\ne 0$,如果检验 ${\lambda }_1=0$，就直接停止检验。后面的检验以此类推。
• 对不为0的典型相关系数对应的典型变量进行分析。

(2)SPSS求解

• step 1：导入数据。
• step 2：检查数据的类型。
  
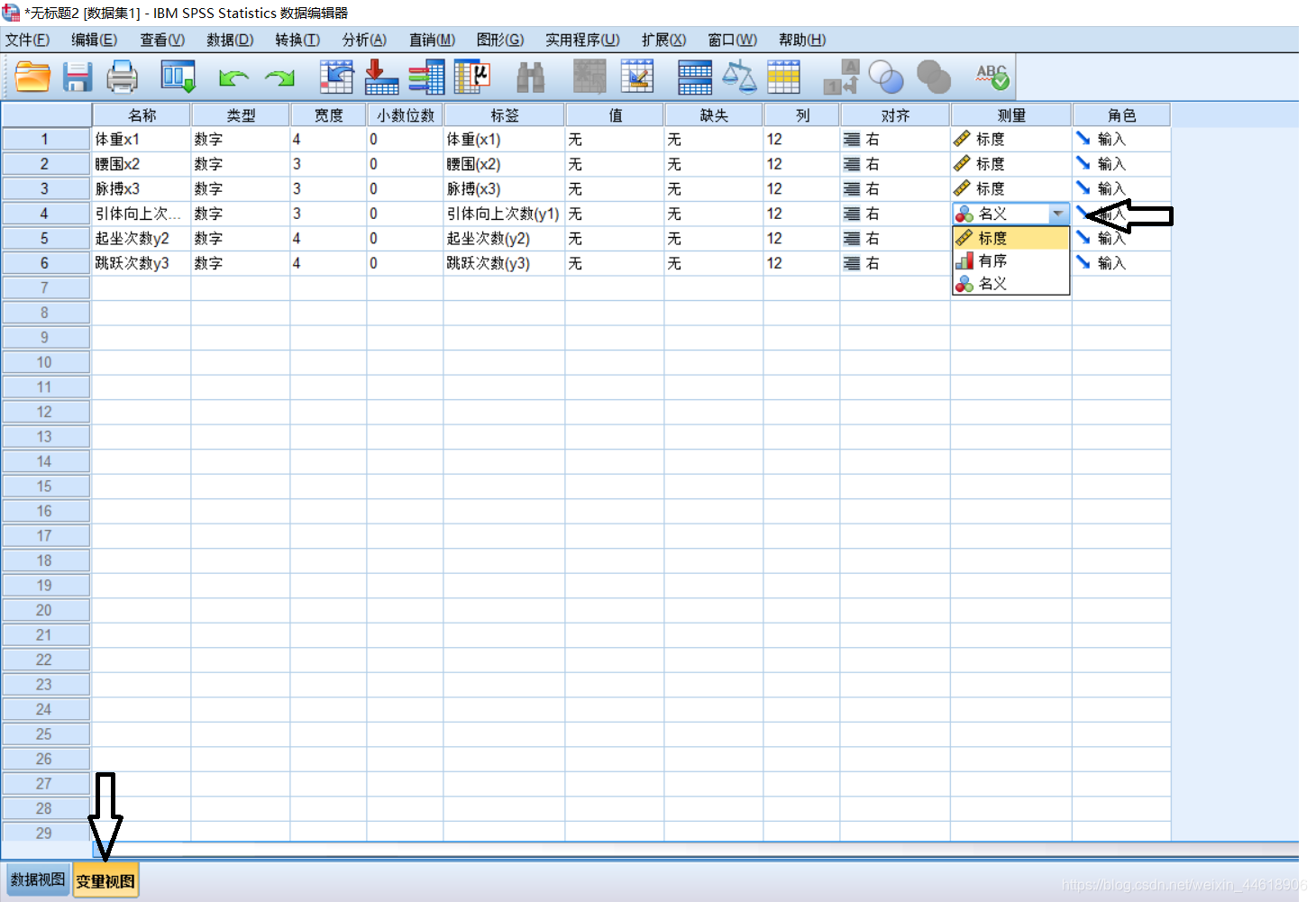
  • 常规的数值类型比如血压，身高等都是标度。
  • 单纯的区分性质的，比如男女等，这是名义。
  • 有顺序区分的，比如甲乙，优良等，这是有序。
• step 3：进行SPSS分析。
  

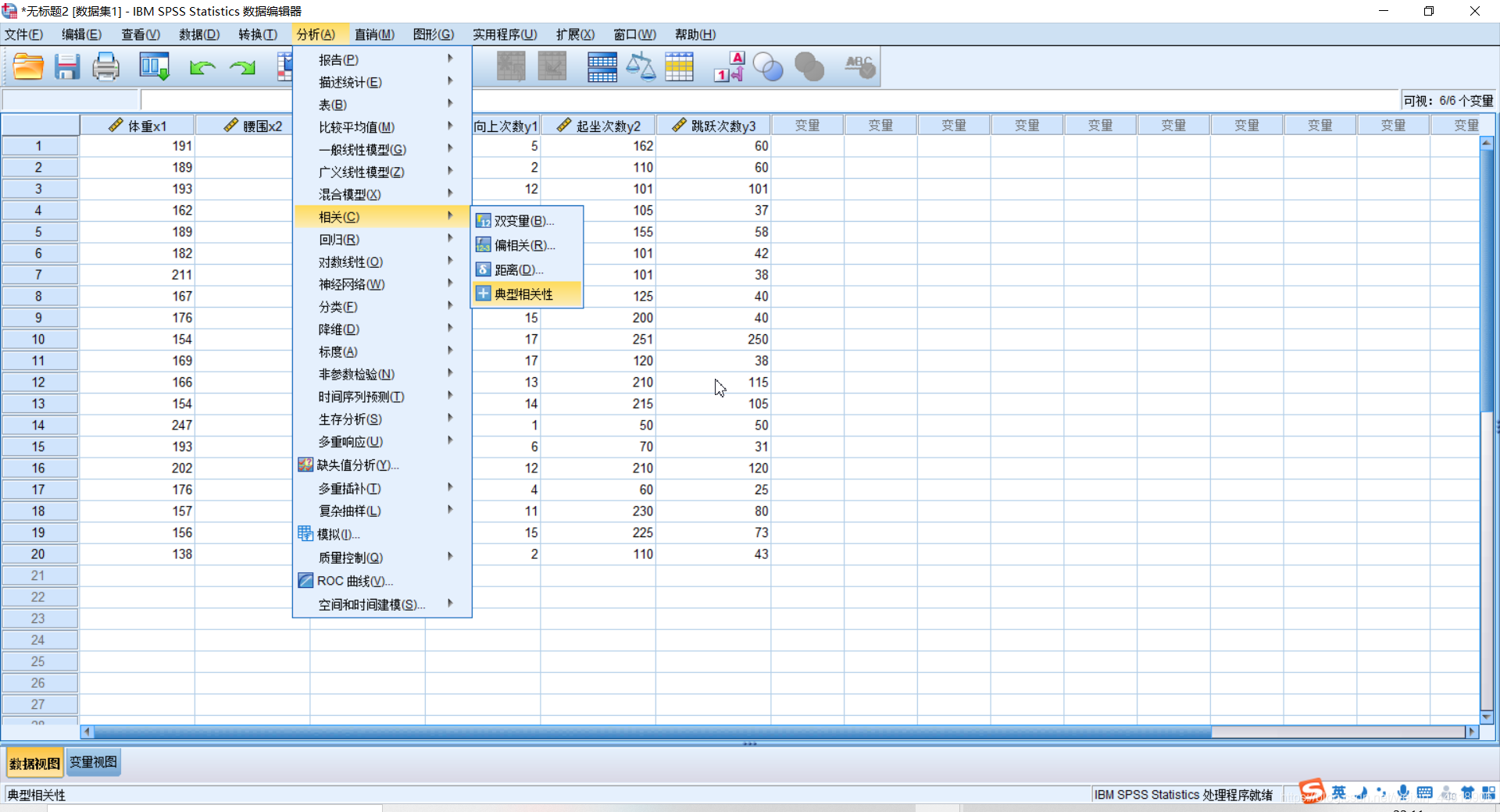
• step 4：导出分析结果。
• step 5：对导出的结果进行分析。

  • 可以看出在 $90\%$ 的置信水平上第一组典型变量是具有相关性的。

    

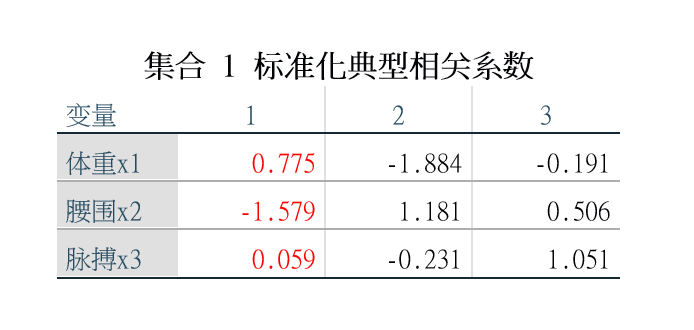
  • 由于只有第一组存在相关性，因此这里也只看第一组，并且要考虑的是标准化的典型相关系数。$$U_1=0.775X_1^{(1)}-1.579X_2^{(1)}+0.059X_3^{(1)}$$$$V_1=0.349X_1^{(2)}+1.054X_2^{(2)}-0.716X_3^{(2)}$$

    
    

  • 这里也只考虑第一组的典型载荷。所谓载荷就是变量与本组集合之间的相关系数。比如体重，腰围，脉搏与生理指标的第一典型变量之间的相关系数，引体向上次数，起坐次数，跳跃次数与训练指标的第一典型变量之间的相关系数。正负号代表正相关还是负相关。生理指标的第一典型变量与体重腰围成负相关，与脉搏成正相关，并与腰围的相关性最大。训练指标的第一典型变量与引体向上次数，起坐次数，跳跃次数成正相关，并与起坐次数的相关性最大，说明减肥主要靠起坐。