多目标优化模型求解方案
文章目录
(1) 概念引入
1.多目标优化模型
- 数学模型(一般都转化成最小问题) min F ( x ) = ( f 1 ( x ) , f 2 ( x ) , … , f m ( x ) ) s . t . x ∈ Ω \min{F(x)}=(f_1(x),f_2(x),\dots,f_m(x))\\ ~~\\ s.t. x\in\Omega minF(x)=(f1(x),f2(x),…,fm(x)) s.t.x∈Ω
- 决策空间: x = ( x 1 , x 2 , … , x n ) x=(x_1,x_2,\dots,x_n) x=(x1,x2,…,xn)所在的空间 Ω \Omega Ω,其中 Ω = { x ∈ R n ∣ g i ( x ) ≤ 0 , i = 1 , 2 , … , p } \Omega=\{x\in R^n|g_i(x)\le0,i=1,2,\dots,p \} Ω={ x∈Rn∣gi(x)≤0,i=1,2,…,p}。
- 目标空间: m m m维向量 F ( x ) F(x) F(x)所在的空间。
2.支配
- 定义1:对最小化问题,一个向量 u = ( u 1 , u 2 , … , u w ) u=(u_1,u_2,\dots,u_w) u=(u1,u2,…,uw) 称为支配(优于)另一个向量 v = ( v 1 , v 2 , … , v w ) v=(v_1,v_2,\dots,v_w) v=(v1,v2,…,vw),当且仅当 u i ≤ v i i = 1 , 2 , ⋯ , m u_i\le v_i i=1,2,\dotsb,m ui≤vii=1,2,⋯,m 且 ∃ j ∈ { 1 , 2 , ⋯ , m } , u j < v j 。 \exist j\in\{1,2,\dotsb,m\},u_j<v_j。 ∃j∈{ 1,2,⋯,m},uj<vj。
- 定义2:对于任意两个自变量向量 x 1 , x 2 ∃ Ω x_1,x_2\exist\Omega x1,x2∃Ω,如果下列条件成立: f i ( x 1 ) ≤ f i ( x 2 ) , ∀ i ∈ { 1 , 2 , ⋯ , m } f j ( x 1 ) ≤ f j ( x 2 ) , ∀ j ∈ { 1 , 2 , ⋯ , m } f_i(x_1)\le f_i(x_2),\forall i\in\{1,2,\dotsb,m\}\\ f_j(x_1)\le f_j(x_2),\forall j\in\{1,2,\dotsb,m\} fi(x1)≤fi(x2),∀i∈{ 1,2,⋯,m}fj(x1)≤fj(x2),∀j∈{ 1,2,⋯,m}则称 x 1 x_1 x1 支配 x 2 x_2 x2。
- 定义3:
- 如果 Q Q Q 中没有支配(优于) x x x 的解,则称 x x x 是问题的一个Pareto最优解。
- Pareto最优解的全体被称作Pareto最优解集;Pareto最优解集在目标函数空间的像集称为Pareto Front(Pareto前沿,阵(界)面)。
(2) 多目标优化的传统解法
- 加权法
- 理想点法(TOPSIS)
- 分层序列法(就是每次先求出一个最优值,然后把这个最优值当作不等式限制)
- 把 m m m 个目标篇按重要程度排序。假定 f 1 ( x ) f_1(x) f1(x) 最重要, f m ( x ) f_m(x) fm(x) 最不重要。
- 先求问题 min f 1 ( x ) s . t . x ∈ Ω \min{f_1(x)}\\s.t. x\in\Omega minf1(x)s.t.x∈Ω 的最优解 x ( 1 ) x^{(1)} x(1) 及最优值 f 1 ∗ f_1^* f1∗。
- 再求问题 min f 2 ( x ) s . t . x ∈ Ω 1 = Ω ∩ { x ∣ f 1 ( x ) ≤ f 1 ∗ } \min{f_2(x)}\\s.t. x\in\Omega_1=\Omega\cap\{x|f_1(x)\le f_1^*\} minf2(x)s.t.x∈Ω1=Ω∩{ x∣f1(x)≤f1∗} 的最优解 x ( 1 ) x^{(1)} x(1) 及最优值 f 1 ∗ f_1^* f1∗。
- 重复上面的步骤。
(3) 智能优化算法
- 这里选取 NSGA-II 方法
- 算法简介
- 首先随机产生种群规模为 N N N 的初始种群 P t P_t Pt,进化代数 t = 0 t=0 t=0。
- 开始循环,对 P t P_t Pt 进行交叉变异操作生成新种群 Q t Q_t Qt。
- 取 R t = P t ∪ Q t R_t=P_t\cup Q_t Rt=Pt∪Qt。
- 对 R t R_t Rt 进行非劣分类。
- 按非劣等级从低到高选出 N N N 个个体填充到 P t + 1 P_{t+1} Pt+1 中。
- 获取 R t R_t Rt 中的第一非劣等级个体集,判断并决定该非劣等级能否全被新种群容纳。如果能,将该非劣等级的所有个体填充到新种群中,继续判断下一非劣等级能否全被新种群容纳。
- 如此反复,直到不能容纳该非劣等级的所有个体,假设为第 i + 1 i+1 i+1 级。对最后不能被完全容纳的非劣组中的个体求其拥挤距离,并选择分布最广的个体填充满新种群。
- 重复
- 快速非支配排序方法
- 首先不被任何点支配的点选出来,成为 F 1 F_1 F1。
- 把选出来的点支配的点的支配关系全部删除,然后再看现在有哪些点不被任何点支配,成为 F 2 F_2 F2.
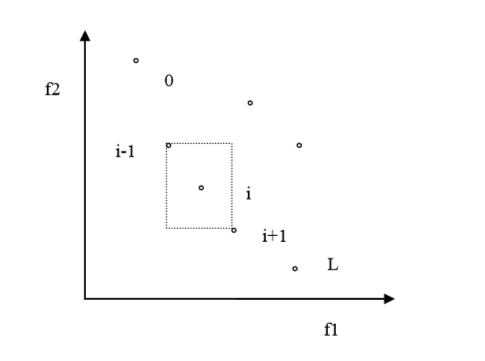
- 拥挤距离 d i = ∑ m = 1 M ∣ f m i + 1 − f m i − 1 ∣ d_i=\sum_{m=1}^{M}|f_m^{i+1}-f_m^{i-1}| di=m=1∑M∣fmi+1−fmi−1∣
- d i d_i di 表示第 i i i 个个体的拥挤距离。
- i − 1 i-1 i−1 和 i + 1 i+1 i+1 是个体 i i i 沿着 i i i 所在的Pareto Front Line 的两边邻近的两个个体。
- f m i + 1 f_m^{i+1} fmi+1 和 f m i − 1 f_m^{i-1} fmi−1 分别表示 i − 1 i-1 i−1 和 i + 1 i+1 i+1 个个体第 m m m 个目标函数值。(下面的图 m = 1 , 2 m=1,2 m=1,2)
(3) matlab的智能优化算法
1. 基本的两个函数
- 参数设置
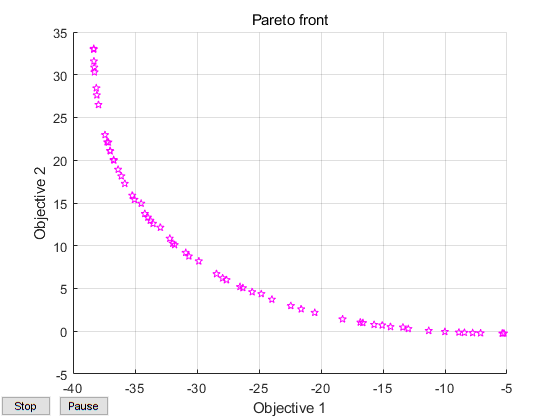
options=gaoptimset('paretoFraction',0.3,'populationsize',100'generations',200,'stallGenLimit',200,'TolFun',1e-10,'PlotFcns',@gaplotpareto);paretoFraction:最优个体系数这里设为0.3populationsize:种群大小这里设为100generations:最大进化代数这里设为200stallGenLimit:停止代数这里设为200TolFun:适应度函数偏差这里设为1e-10gaplotpareto:绘制Pareto前沿
- 函数引用
[X,FVAL]=gamultiobj(fitnessfcn,nvars,A,b, Aeq,beq,lb,ub,nonlcon,options))fitnessfcn:函数句柄。nvars:变量个数。ub,lb:上下限。A,b:线性不等式约束。Aeq,beq:线性等式约束。
2. 例子
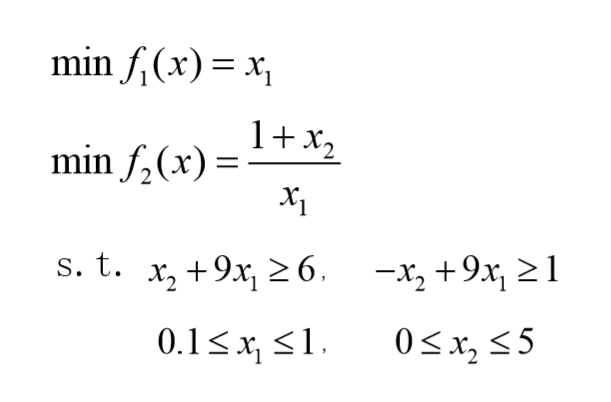
- 函数定义
%%这里定义该函数
function y=Fun(x)
y(1)=x(1);
y(2)=(1+x(2))/x(1);
- 进行计算
%%这里赋初值并且进行多目标优化的计算
fitnessfcn=@Fun;
nvars=2;
lb=[0.1,0];
ub=[1,5];
A=[-9,-1;-9,1];
b=[-6;-1];
Aeq=[];
beq=[];
options=gaoptimset('paretoFraction',0.4,'populationsize',200,'generations',300,'stallGenLimit',300,'TolFun',1e-10,'PlotFcns',@gaplotpareto);
[x,fval]=gamultiobj(fitnessfcn,nvars,A,b,Aeq,beq,lb,ub,options)
- 结果
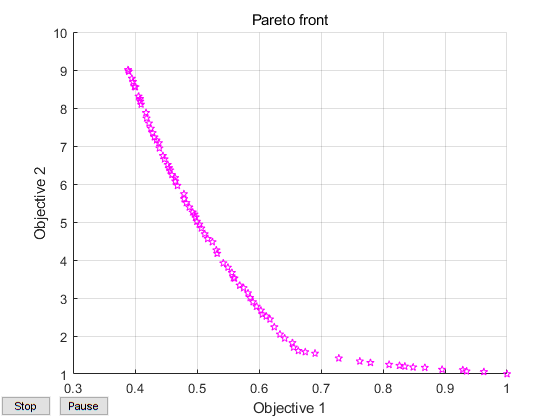
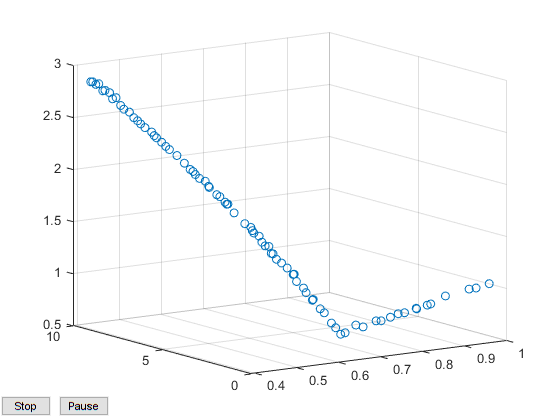
3. 如果有三个目标
- 可以先优化出来,得到
fval然后用scatter3进行绘制。 - 对上面的问题增加条件 m i n x 1 + x 2 min~{x_1+x_2} min x1+x2
- 增加
scatter3(fval(:,1),fval(:,2),fval(:,3)) - 得到结果