建模算法整理,文章主要介绍了 模糊综合评价的二级模糊评价,在上一篇的一级模糊评价上的改进。
参考学习资料:清风数学建模 数学建模算法与程序
其他资源:2016到2020美赛o奖论文=== 姜启源 司守奎电子书===论文模板 ====算法代码
如果需要可私信或者评论
往期文章链接:
1 为什么引入"多级"模糊评价模型
因素(指标)集合中元素过多,我们可以对其进行归类。归类后可以简化我们的计算
2 二级模糊综合评价模型步骤
2.1 概述说明
二级模糊综合评价步骤和一级模糊综合评价步骤一致,从计算一个矩阵到计算多个矩阵。掌握好一级模糊综合评价的步骤就很容易。
2.2 划分因素集
要求:不同子集元素互不相同
Ui={u1,u2,…un} 表示二级因素集
U={U1,U2,…Uk} 表示一级因素集
2.3 确定评语集V{}并对二级因素集进行评判得到综合评判矩阵
V = {v1,v2,…vm}
Bi = Ai * Ri (i = 1,2,…k)

2.4 再对第一级元素U{}进行综合评判
若权重A={a1,a2,…ak}
则综合评判为 B = A * R
2.5 按最大隶属度原则确定相应评语或等级
3 具体案例带入数值计算
3.1 题目:评价学生表现并作为奖学金的评判标准
3.2 划分因素集并标注了对应权重
说明:权重可以通过层次分析法或者熵权法获得,步骤省略,可以参考往期文章。
因素集划分如下

3.3 确定评语集V 并对二级因素集进行评判得到综合评判矩阵
3.3.1 假设评语集
V={一等奖学金v1,二等奖学金v2,无奖学金v3}
3.3.2 模糊统计法(投票)得到R1

3.3.3 解释说明R1矩阵数据
单从专业课成绩来看,这位同学在评语集一等奖学金隶属度0.8,二等奖学金隶属度0.2,无奖学金的隶属度为0。
同理可以解释矩阵的其他元素。
3.3.4 通过A1权重和R1求的综合评判矩阵B1
A1 =[0.6 ,0.4 ]
B1 = A1*R1=[0.76 0.24 0]
3.3.5 解释说明B1矩阵数据
这位同学单看成绩这一个因素,获得一等奖学金的隶属度为0.76,获得二等奖学金的隶属度为0.27,无奖学金的隶属度为0。
3.3.6 同理可以求的 B2,B3,B4 对应二级的另外三个模块
B2 = [0.15 0.27 0.58 ]
B3 = [0.4 0.2 0.4 ]
B4 = [0.1 0.8 0.1 ]
3.3.7 通过一级元素进行综合评判(通过B1 B2 B3 B4 构成新的模糊综合评判矩阵)
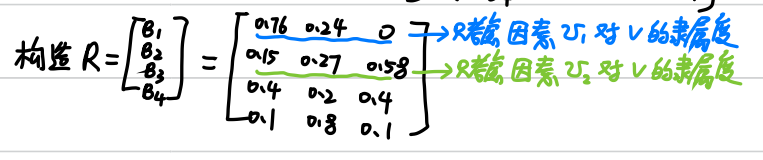
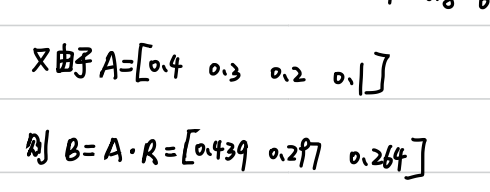
3.4 按最大隶属度原则确定相应评语或等级(写结论)
由于0.439最大,即获得一等奖学金的隶属度最大,所有该同学应评为一等奖学金。
4 总结
文章纯属建模学习整理。
最后希望给文章点个赞,整理不易!!!
最后希望给文章点个赞,整理不易!!!
最后希望给文章点个赞,整理不易!!!
