学习链接

https://study.163.com/course/courseMain.htm?courseId=1004570029

机器学习的定义

监督学习

无监督学习

代价函数

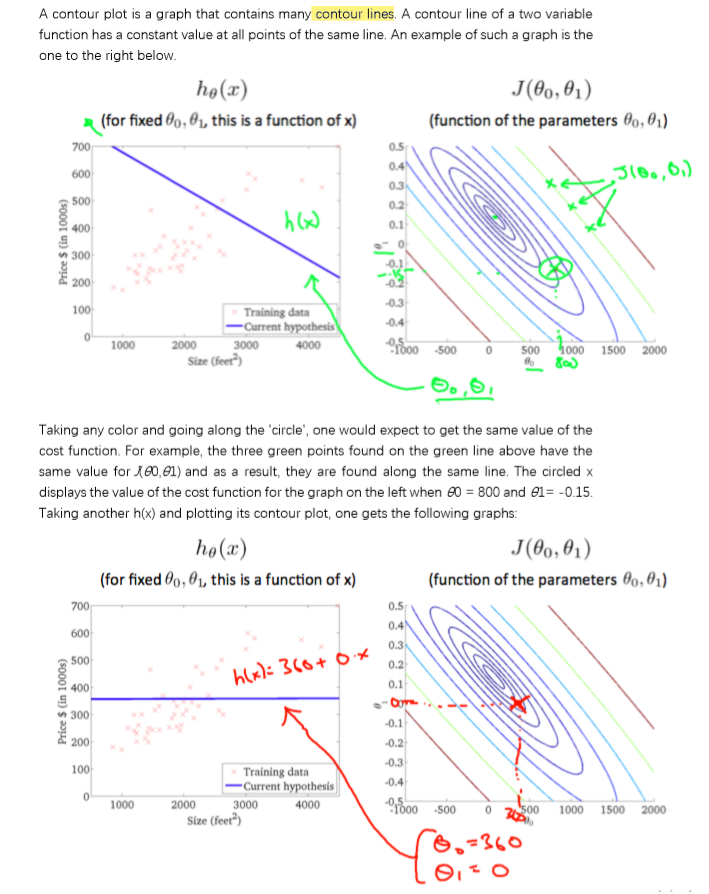
梯度下降

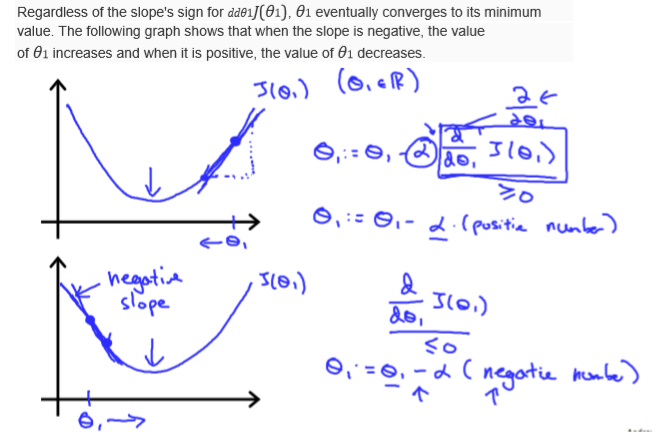
注意：同步更新参数！

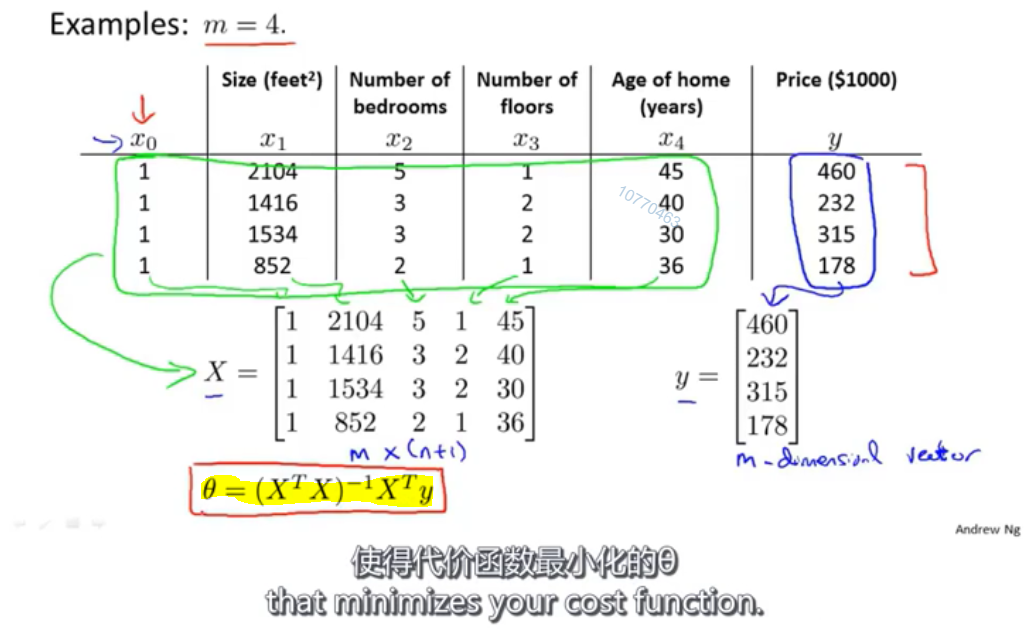
多特征 & 多样本

特征缩放（加速梯度下降）

Notes：也适用于 Logistic 回归

学习速率选择的技巧（画出代价函数随着迭代次数增加而变化的图）

特征的选择

多项式回归

正规方程：

Notes：

如果使用正规方程求解最优参数，不需要进行特征缩放
梯度下降适用于大部分模型的参数优化，而正规方程只适用于线性回归的参数优化

正规方程中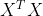（ $X^TX$ ）这一项不可逆的原因 & 解决方案

向量化的表示法

Logistic Function & Sigmoid Function

Notes：Logistic Regression 虽然翻译为逻辑回归，但它是一个 classification problem

决策边界

Notes：The decision boundary is the line that separates the area where y = 0 and where y = 1. It is created by our hypothesis function

Logistic 回归的代价函数

因为引入了 Sigmoid Function，Cost Function 关于参数 θ 的图像是 non-convex 的。所以使用梯度下降不一定能收敛到 global minima，可能在 local minima 就停了。

写成紧凑一点的形式，用一个式子表达：

Logistic 回归之梯度下降

高级的参数优化算法

Notes：

感觉有点像加强版的 GD 算法，但不用自己选择学习速率（待确定）
Octave / Matlab 的 fminunc() 函数就是干这个事儿的

多元分类器

过拟合 & 欠拟合

Notes：过拟合又叫 high variance；欠拟合又叫 high bias

过拟合的解决方法

正则化

Notes：

1、为了使正则化运作良好，我们应该去选择一个不错的正则化参数 λ （如何选择待查询和学习）

2、注意正则化时，不去处理偏置项

线性回归的正则化（梯度下降、正规方程）

逻辑回归的正则化

为什么引入神经网络？

因为当样本特征 n 特别多的时候，逻辑回归要学习的参数太多了。eg：图中 n = 100，二次项的参数就有约 5000 个；三次项的参数就有约 170000 个。

、

如果在计算机视觉领域中使用逻辑回归的话，参数更加是爆炸性增长。

思想 / 理论：当我们把任意一个传感器接入大脑中，大脑都能学会如何处理它所接收到的数据

神经元模型

神经网络

Notes：

隐藏层和激活函数的关系：隐藏层可以设置激活函数，也可以不设置激活函数。如果设置激活函数，就为模型添加非线性因素。

前向传播（向量表示）

一些简单神经网络例子的直观理解

多元分类

注意：h(x) 的结果不再是一个数字，而是向量（最后向量的维度由分类的类数决定）

反向传播算法

Notes：

反向传播法是梯度下降法在深度网络上的具体实现方式。
找到一份很棒的通俗易懂解释 BP 原理以及计算步骤的材料：https://blog.csdn.net/ft_sunshine/article/details/90221691
吴恩达视频中关于反向传播的公式推导：https://blog.csdn.net/xuan_liu123/article/details/83660316

梯度检验（用来验证反向传播算法的正确性）

Notes：

自己总结：根据输入 X，Θ 前向传播算出代价函数 J(Θ) 的值，再算出反向传播的梯度值 $\frac{\partial J}{\partial \Theta}$ (grad)。同时，根据梯度检验的公式，算出在该 Θ 下的梯度检验值 (grad_difference)，最后相减（grad_difference - grad），看差值的绝对值是否小于 $10^{-7}$ 来验证梯度值 $\frac{\partial J}{\partial \Theta}$ (grad) 的正确性。
补充学习链接：
1. https://blog.csdn.net/lanchunhui/article/details/51279293
2. https://blog.csdn.net/u011324454/article/details/78648656

随机初始化参数

组合到一起（选择网络架构、）

应用机器学习的建议

1、评估模型（留出法）

2、模型选择问题（验证集调参法）

Notes：总的来说，验证集用来选模型，测试集用来评估最后选出来的那个模型的泛化能力

3、偏差（欠拟合）和方差（过拟合）的诊断

4、正则化与偏差（欠拟合）和方差（过拟合）的关系

注意： $J_{train}\left ( \Theta \right )$ 和 $J\left ( \Theta \right )$ 不同

5、学习曲线

作用：提高算法的性能 / 看看算法是否正确运行

如果遇到了 high bias（欠拟合）的情况，就别浪时间 collect more data 了

确定这些解决方法适用于哪些问题

总结

机器学习系统设计

误差分析

Note：误差分析要在验证集上做，而不是测试集！

不对称性分类的误差评估

skewed classes（偏斜类）：就是数据分布不均匀的情况，就是存在测试集或者训练集中某一类样本特别多，其他类样本特别少的情况。这个时候再用 Accuracy 来衡量算法的准确性就不太合适了

precision：查准率 recall：召回率

查准率和召回率的权衡

推导过程：

如果是希望在非常自信的情况下，才预测为 1，那么 predicted class = 1 （TP + FP）的数目会少很多， predicted class = 0 （TN + FN）的数目会多很多。所以，precision 的分母会小很多，整个 precision 就很高；
如果是保守预测，尽可能减小 FN 的个数，减小错过治疗的机会的情况下， predicted class = 1 （TP + FP）的数目会多很多，precision 的分母会大很多，整个 precision 就会很小；

如果对模型没有特别的要求（特别的要求指的是如上面两种情况），可以用 F1-score 来帮助我们选择 threshold