建模算法整理,文章主要介绍了 TOPSIS法,主要用于解决评价类问题。
参考学习资料:清风数学建模
其他资源:2016到2020美赛o奖论文=== 姜启源 司守奎电子书===论文模板 ====算法代码
如果需要可私信或者评论
文章目录
TOPSIS法介绍
TOPSIS法(Technique for Order Preference by Similarity to Ideal Solution)
可翻译为逼近理想解排序法,国内常简称为优劣解距离法
TOPSIS 法是一种常用的综合评价方法,其能充分利用原始数据的信息,
其结果能精确地反映各评价方案之间的差距。
层次分析法的一些局限性[引出本文]
-评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异
可能会很大。

- 如果决策层中指标的数据是已知的,那么我们如何利用这些数据来使得
评价的更加准确呢?

例子:单个指标的一种计算评分方式
小明同宿舍共有四名同学,他们第一学期的高数成绩如下表所示:

请你为这四名同学进行评分,该评分能合理的描述其高数成绩的高低。
方式一:

缺陷明显:可以随便修改成绩,只要保证排名不变,那么评分就不会改变!

方法二(正确的方式):
-
确定最高成绩:max:99
-
确定最低成绩:min:90
-
构建计算评分的公式: x − m i n m a x − m i n \frac{x-min}{max-min} max−minx−min
-
重新计算

-
补充说明:为什么不采用 x − 0 100 − 0 \frac{x-0}{100-0} 100−0x−0的计算评分方式如下

解释:- 比较的对象一般要远大于两个。(例如比较一个班级的成绩)
- 比较的指标也往往不只是一个方面的,例如成绩、工时数、课 外竞赛得分等。
- 有很多指标不存在理论上的最大值和最小值,例如衡量经济增 长水平的指标:GDP增速。
多个指标的完整处理步骤
将原始矩阵正向化
概述: 所谓的将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标。
四种情况:

极小型指标 ->极大型指标

中间型指标 ->极大型指标

区间型指标 ->极大型指标

正向化矩阵标准化
目的: 消除不同指标量纲的影响

计算得分并归一化(参考例子)



扩展-带权重的TOPSIS
修改前步骤三

修改后步骤三

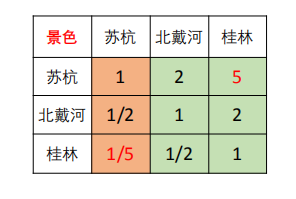
层次分析法求权重

例子(算术平均法 其他两种方式不做说明)


基于熵权法对Topsis模型的修正(承上)
概述 :判断矩阵的确定依赖于专家,如果专家的判断存在主观性的话,会对结果产生很大的影响。(主观性太强)
熵权法:是一种客观赋权方法依据的原理: 指标的变异程度越小,所反映的信息量也越少,其对应
的权值也应该越低。(客观 = 数据本身就可以告诉我们权重)
(一种极端的例子:对于所有的样本而言,这个指标都是相同的数值,
那么我们可认为这个指标的权值为0,即这个指标对于我们的评价起不
到任何帮助)
未完待续…
总结
文章纯属建模学习整理。
最后希望给文章点个赞,整理不易!!!
最后希望给文章点个赞,整理不易!!!
最后希望给文章点个赞,整理不易!!!