【论文阅读笔记】Simple and Deep Graph Convolutional Networks
1. 论文地址:
论文:https://arxiv.org/pdf/2007.02133.pdf
源码:https: //github.com/chennnM/GCNII
2. 摘要:
图卷积网络(GCNs)是一种针对图结构数据的强大的深度学习方法。最近,GCNs和后续的变体在实际数据集中的各种应用领域显示了优越的性能。尽管他们很成功,但是由于过度平滑的问题,大多数目前的GCN模型都是浅层的。
本文研究了深度图卷积网络的设计与分析问题,并提出了GCNII,它是普通GCN模型的扩展,应用了两种简单而有效的技术:初始残差(Initial residual)和恒等映射(Identity mapping)。理论和实践证明,这两种技术有效地缓解了过度平滑的问题,并且深层GCNII模型在各种半监督和完全监督任务上的性能优于最新的方法。
3. 简介:
3.1 图卷积神经网络:
图卷积神经网络(GCN)从CNN演化而来,即通过一组共享的权重参数来对每个节点的邻居做线性变换,然后加上非线性激活函数来获取图节点的特征表示。并且后续研究表明,GCN在社交网络分析、推荐系统等方向都有很大的应用价值。
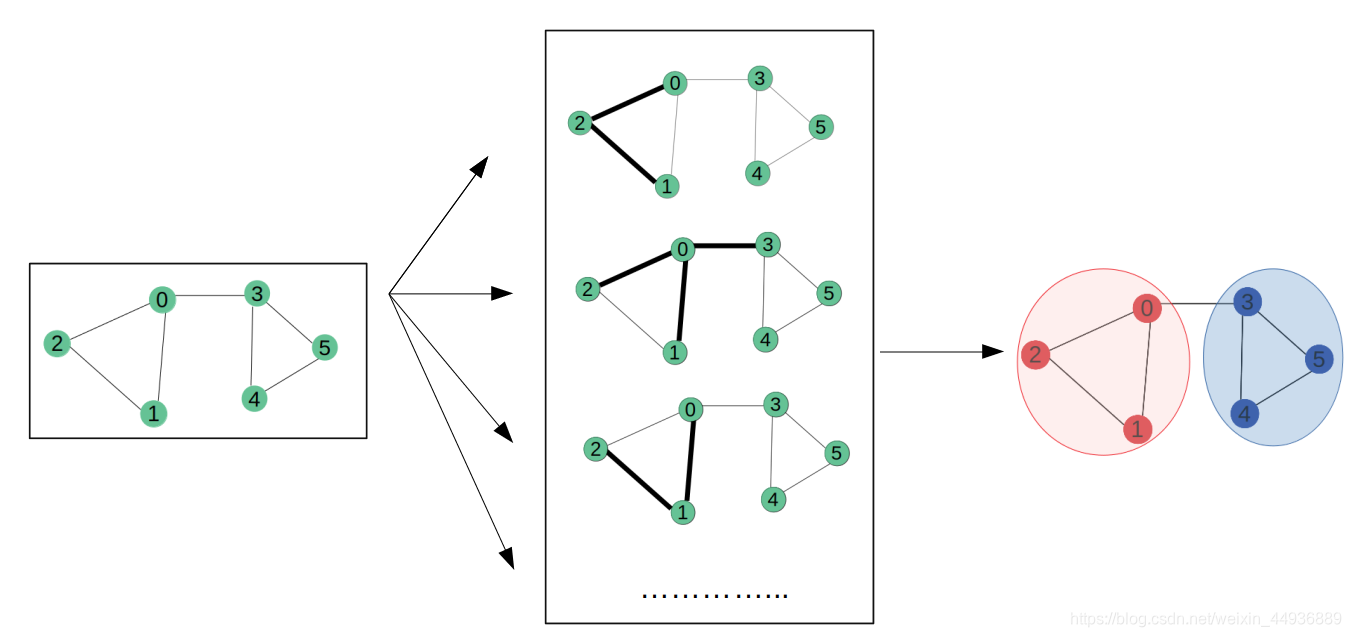
3.2 传统GCN的局限性:
目前的大部分模型(如GCN和GAT),都是使用了较浅的结构设计,并且一般都是用2层卷积实现。这种浅层设计就这限制了它们从高阶邻居中提取高层信息的能力。
然而不管是更多层数或者添加非线性变换。都会导致模型的准确性降低,这种现象就被称作过度平滑(oner-smoothing),即随着层数的增加,GCN节点的表示趋向于收敛到一个特定值,并因此难以区分。
在计算机视觉中,ResNet通过残差结构解决了类似的问题,从而使得能够训练更深层的网络:
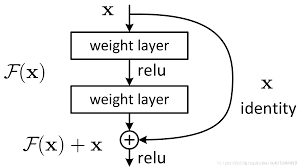
不过在GCN中添加残差结构仅仅能够减缓过度平滑现象,而非从根本上解决这个问题。因此2层以上的GCN模型依然面临的过拟合的问题。
3.3 一些解决方案:
最近的一些模型也在试图解决过度平滑的问题。JKNet使用密集跳跃连接组合每一层的输出,以保持节点表示的位置。DropEdge提出,通过从输入图中随机删除一些边,可以减轻过度平滑的影响。并且实验表明,随着网络深度的增加,这两种方法可以降低性能下降的速度。
然而,对于半监督的任务,最先进的结果仍然是通过浅层模型实现的,因此增加网络深度所带来的效益仍然存在疑问。
另一方面,有几种方法将深度传播与浅神经网络相结合。SGC试图通过在单个神经网络层中应用图卷积矩阵的 k k k 次幂来捕获图中的高阶信息。PPNP和APPNP用自定义的PageRank矩阵代替图卷积矩阵的幂来解决过平滑问题。GDC进一步扩展了APPNP,将自定义PageRank推广到任意图扩散过程。但是,这些方法只是将每一层的相邻特征进行线性组合,而失去了深度非线性架构强大的表达能力,仍然是浅模型。
总之,如何设计一个GCN模型来有效地防止过度平滑,并在真正深度的网络结构中实现最先进的结果,仍然是一个有待解决的问题。由于这一挑战,在设计新的图形神经网络时,网络深度究竟是一种资源还是一种负担甚至还不清楚。
3.4 本文的方案:
本文通过证明普通的GCN 可以通过两个简单而有效的修改扩展到一个深层模型,从而对这个开放问题给出了一个肯定的答案。并且作者还提出了一个应用初始残差和恒等映射的图卷积网络GCNII,来解决过度平滑问题。
在每一层,初始残差从输入层构建一个跳跃连接,而恒等映射在权值矩阵中添加一个单位矩阵。实验研究表明,当我们增加GCNII的网络深度时,这两种简单的技术可以有效地防止过度平滑,并一致地提高其性能。
其次,本文也对多层GCN和GCNII模型进行了理论分析。已知叠加 K K K 层的GCN本质上模拟了一个具有预定系数的 K K K 阶多项式滤波器。之前的研究指出,该滤波器模拟了一个懒惰的随机游走(lazy random walk),最终收敛到平稳向量,从而导致过平滑。
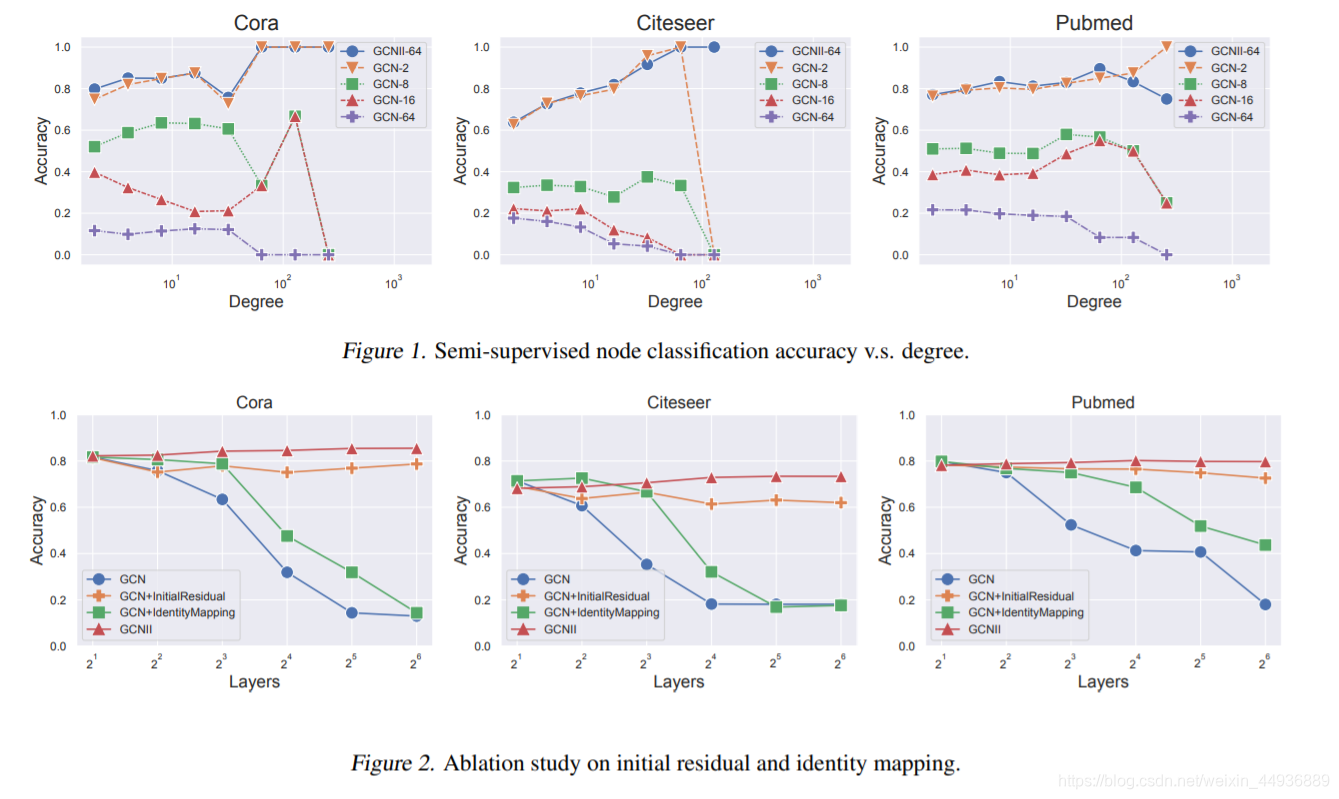
并且本文还证明了 K K K 层GCNII模型可以表示任意系数的 K K K 阶多项式谱滤波器。这个特性对于设计深度神经网络是必不可少的。并且作者还推导了平稳向量的封闭形式,并分析了普通GCN的收敛速度。分析表明,在多层GCN模型中,度比较大的节点更有可能出现过度平滑的现象。
4. 相关研究:
4.1 符号表示:
-
假定一个简单的无向图 G = ( V , E ) G=(V,E) G=(V,E),该图有 n n n 个节点和 m m m 条边。我们将自循环图(self-looped graph)定义为在G中的每个节点上都有一个自循环的图,即 G ~ = ( V , E ~ ) \widetilde{G}=(V,\widetilde{E}) G =(V,E )。
-
我们用 { 1 , . . . , n } \lbrace 1,...,n\rbrace { 1,...,n} 来表示 G G G 和 G ~ \widetilde{G} G 中节点的 I D ID ID,用 d j d_j dj 和 d j + 1 d_j+1 dj+1 分别表示 G G G 和 G ~ \widetilde{G} G 中节点 j j j 的度。
-
并且假定 G G G 中 A A A 为邻接矩阵, D D D 为对角度矩阵,那么 G ~ \widetilde{G} G 的邻接矩阵和对角度矩阵就分别定义为 A ~ = A + I \widetilde{A}=A+I A =A+I 和 D ~ = D + I \widetilde{D}=D+I D =D+I。
-
假设 X ∈ R n × d X\in R^{n×d} X∈Rn×d 为节点的特征矩阵,那么因此每个节点 v v v 都跟一个 d d d 维的特征向量 X v X_v Xv 相关。
-
标准化图拉普拉斯矩阵定义为 L = I n − D − 1 / 2 A D − 1 / 2 L=I_n-D^{-1/2}AD^{-1/2} L=In−D−1/2AD−1/2,是具有特征分解 U Λ U T UΛU^T UΛUT 的对称正半正定矩阵。
4.2 GCN:
之前的研究表明,图的卷积运算可以用拉普拉斯 K K K阶多项式近似表示: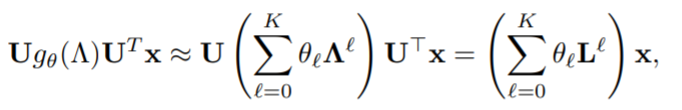
其中 θ ∈ R K + 1 \theta \in R^{K+1} θ∈RK+1 对应于多项式系数的向量。最初的GCN设置 K = 1 K=1 K=1, θ 0 = 2 θ \theta_0=2\theta θ0=2θ, θ 1 = − θ \theta_1=-\theta θ1=−θ,从而定义了卷积操作,即 g θ ∗ x = θ ( I + D − 1 / 2 A D − 1 / 2 ) x g_{\theta}*x=\theta(I+D^{-1/2}AD^{-1/2})x gθ∗x=θ(I+D−1/2AD−1/2)x。
然后通过再归一化策略,可以将矩阵 I + D − 1 / 2 A D − 1 / 2 I+D^{-1/2}AD^{-1/2} I+D−1/2AD−1/2 替换为归一化的版本,即 P ~ = D ~ − 1 / 2 A ~ D ~ − 1 / 2 = ( D − 1 / 2 + I n ) ( A + I n ) ( D − 1 / 2 + I n ) \widetilde{P}=\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2}=(D^{-1/2}+I_n)(A+I_n)(D^{-1/2}+I_n) P
=D
−1/2A
D
−1/2=(D−1/2+In)(A+In)(D−1/2+In)。由此可以定义图卷积操作:
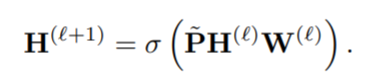
其中 σ \sigma σ 是 R e L U ReLU ReLU 激活函数。
SGC论文中表明, K K K 层的GCN对应于图 G ~ \widetilde{G} G 的频谱域上一个固定的 K K K 阶多项式滤波器。
假设 L ~ = I n − D ~ − 1 / 2 A ~ D ~ − 1 / 2 \widetilde{L}=I_n-\widetilde{D}^{-1/2}\widetilde{A}\widetilde{D}^{-1/2} L =In−D −1/2A D −1/2 为自循环图 G ~ \widetilde{G} G 的归一化拉普拉斯矩阵,那么对于 K K K 层GCN上的信号 x x x 有:
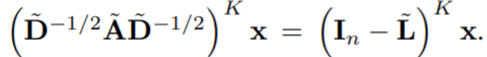
这就表明通过在每个节点上添加自身环, L ~ \widetilde{L} L 有效地缩小基础图的频谱。
5. GCNII 模型:
5.1 模型简介:
我们已知 K K K 层GCN在图 G ~ \widetilde{G} G 的谱域上模拟了一个系数固定的 K K K 阶多项式滤波器 ( ∑ l = 0 K θ l L ~ l ) x (\sum^K_{l=0}\theta_l\widetilde{L}^l)x (∑l=0KθlL l)x。而固定的系数限制了多层GCN模型的表达能力,从而导致过度平滑。
为了将GCN扩展到深层模型,我们需要使GCN能够表达一个具有任意系数的 K K K 阶多项式滤波器。本文证明这可以通过两种简单的技术来实现:初始残差连接和恒等映射。
形式上,我们将GCNII的第1层定义为:
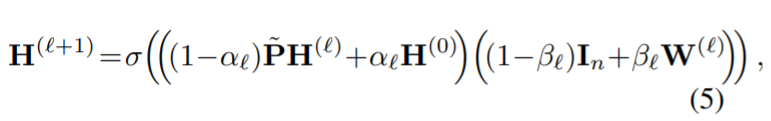
其中 α l \alpha_l αl 和 β l \beta_l βl 是后续需要讨论的两个超参数。该方法相比于GCN模型主要有两处改进:
- 将带有初始残差连接的平滑表示 P ~ H ( l ) \widetilde{P}H^{(l)} P H(l) 与第一层 H ( 0 ) H^{(0)} H(0) 结合;
- 在第 l l l 个权重矩阵 W ( l ) W^{(l)} W(l) 上面添加了一个恒等映射 I n I_n In;
5.2 初始残差连接:
为了模拟ResNet中的残差结构,GCN中提出可以将结合平滑表示 P ~ H ( l ) \widetilde{P}H^{(l)} P H(l) 与 H ( l ) H^{(l)} H(l) 结合。然而这样的连接操作只是部分程度上减轻了过度平滑的问题,随着层数加深模型准确率依然会下降。
因此作者建议,与其使用剩余连接来融合来自前一层的信息,不如构建一个与初始表示 H ( 0 ) H^{(0)} H(0) 的连接。初始残差连接确保了即使我们堆叠了许多层,每个节点的最终表示也都至少保留了来自输入层的部分 α l \alpha_l αl 输入。
在实践中,我们可以简单地设置 α l = 0.1 \alpha_l=0.1 αl=0.1 或 α l = 0.1 \alpha_l=0.1 αl=0.1,这样每个节点的最终表示至少包含输入特征的一部分。
5.3 恒等映射:
恒等映射同样借鉴于ResNet。在第 l l l 层中,作者在权重 W ( l ) W^{(l)} W(l) 中添加了一个单位矩阵 I n I_n In,原因如下:
- 跟ResNet类似,恒等映射保证了深度模型至少与浅层模型准确率相同。即假设 β l \beta_l βl 足够小,模型就会忽略权重矩阵 W ( l ) W^{(l)} W(l)。
- 之前的研究表明,在半监督任务中,特征矩阵的不同维数之间频繁的相互作用会降低模型的性能。直接将平滑表示 P ~ H ( l ) \widetilde{P}H^{(l)} P H(l) 映射到输出中会减小类似的交互。
- 恒等映射被证明在半监督学习中非常有效。假如我们将ResNet写成 H ( l + 1 ) = H ( l ) ( W ( l ) + I n ) H^{(l+1)}=H^{(l)}(W^{(l)}+I_n) H(l+1)=H(l)(W(l)+In) ,那么它满足以下性质:(1)最优权矩阵 W ( l ) W^{(l)} W(l) 具有较小的范数;(2) 唯一的临界点是全局最小值;第一条性质允许我们对 W ( l ) W^{(l)} W(l) 进行强正则化以避免过拟合,第二条性质在训练数据有限的半监督任务中是可取的。
- Oono和Suzuki等人从理论上证明了 K K K 层GCN的节点特征会收敛到一个子空间,从而导致信息丢失。并且收敛率取决于 s K s^K sK, s s s 为权矩阵 W ( l ) W^{(l)} W(l) 的最大奇异值, l = 0 , . . . , K − 1 l=0,...,K-1 l=0,...,K−1。通过将 W ( l ) W^{(l)} W(l) 替换为 ( 1 − β l ) I n + β l W ( l ) (1-\beta_l)I_n+\beta_l W^{(l)} (1−βl)In+βlW(l) 并且在 W ( l ) W^{(l)} W(l) 上应用正则化,我们可以将 W ( l ) W^{(l)} W(l) 的范数变得很小, ( 1 − β l ) I n + β l W ( l ) (1-\beta_l)I_n+\beta_l W^{(l)} (1−βl)In+βlW(l) 的奇异值会接近于 1 1 1。因此最大奇异值 s s s 也会接近于 1 1 1,从而防止 s K s^K sK 变得很大,并且减轻了信息丢失。
其中设置 β l \beta_l βl 的原则是确保权重矩阵的衰减随着堆叠的层数增加而自适应地增加。在实际中,作者设置 β l = l o g ( λ l + 1 ) ≈ λ l \beta_l=log(\frac{\lambda}{l}+1)\approx\frac{\lambda}{l} βl=log(lλ+1)≈lλ , λ \lambda λ 为超参数。
5.4 迭代收缩阈值:
近几年的研究在网络结构设计方面进行了一些优化。其思想是将前馈神经网络看作是一种最小化函数的迭代优化算法,并假设优化算法越好,网络结构越好。因此,数值优化算法的理论可以启发设计更好和更可解释的网络结构。
本文的恒等映射映射在结构中的使用也是出于这个原因。作者考虑Lasso算法(英语:least absolute shrinkage and selection operator,又译最小绝对值收敛和选择算子、套索算法)的目标函数为:
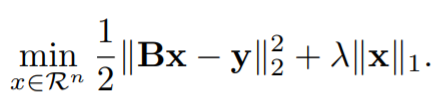
与压缩感知相似,假定 x x x 是我们试图恢复的信号, B B B 是测量矩阵, y y y 是我们观察到的信号。在GCN中, y y y 是节点的原始特征, x x x 是网络试图学习的节点嵌入。与标准回归模型相反,设计矩阵 B 是 B是 B是 未知参数,将通过反向传播来学习。
因此,这与已经被用来设计和分析CNN的稀疏编码问题的核心思想是一致的。迭代收缩阈值法是解决上述优化问题的有效算法,其中第 ( t + 1 ) (t + 1) (t+1)次迭代更新为:
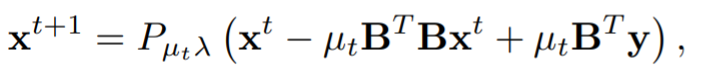
其中 μ t \mu_t μt 是步数大小, P β ( ⋅ ) P_{\beta}(·) Pβ(⋅) 是entry-wise soft thresholding function:
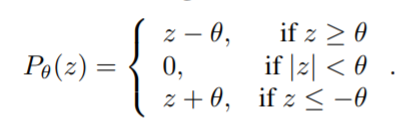
那么如果我们现在用 W W W 重置参数 − B B T -BB^T −BBT,上述更新方程就跟本文的方法非常类似了,即 x t + 1 = P μ t λ ( ( I + μ t W ) x t + μ t B T y ) x^{t+1}=P_{\mu_t\lambda}((I+\mu_tW)x^t+\mu_tB^Ty) xt+1=Pμtλ((I+μtW)xt+μtBTy),其中 μ t B T y \mu_tB^Ty μtBTy 表示初始的残差, I + μ t W I+\mu_tW I+μtW 表示恒等映射。
soft thresholding算子作为非线性激活函数,类似于ReLU激活的效果。综上所述,本文的GCNII,特别是恒等映射的使用,是基于迭代收缩阈值算法来解决LASSO的。
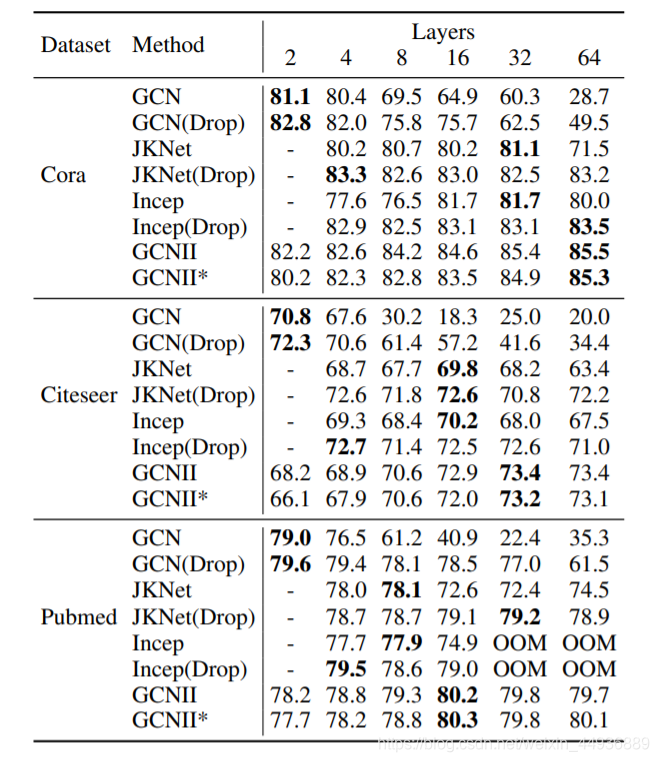
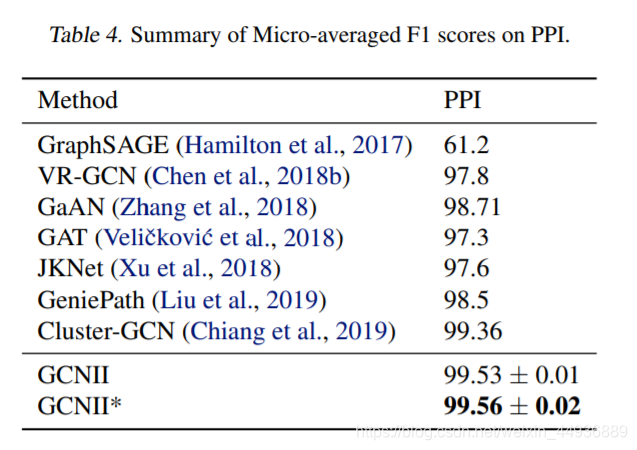
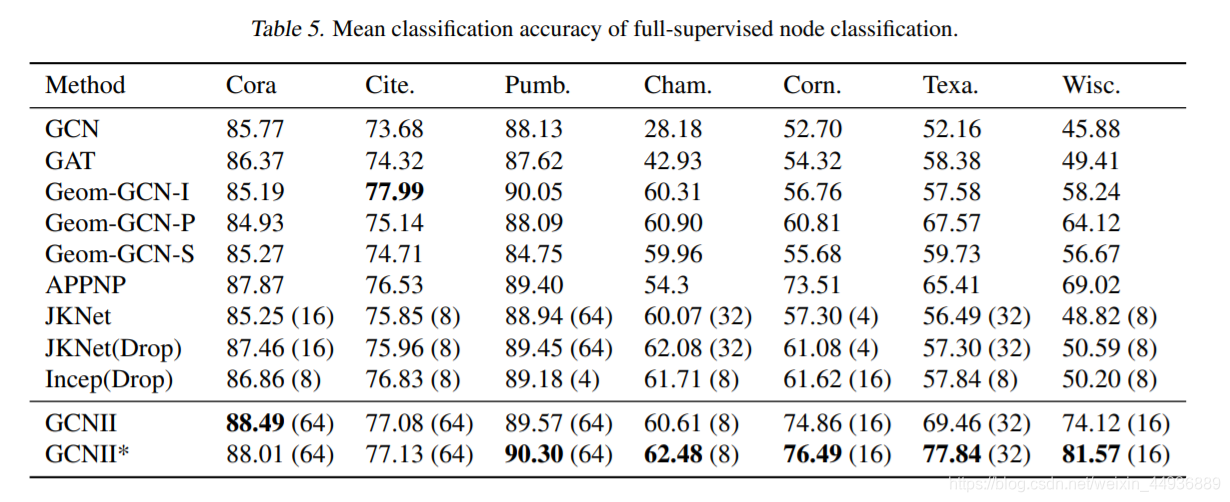
6. 实验结果:
关注我的公众号:
感兴趣的同学关注我的公众号——可达鸭的深度学习教程:
