1. ceil、floor和round的功能
首先,这三个方法都是Math类的静态方法,而且类Math在java.lang包下,所以我们在代码中可以直接调用Math的方法。
Math.ceil(double a)实现的是对小数向右取整,如 Math.ceil(-0.7) = -0.0,Math.ceil(0.5) = 1.0, Math.ceil(1.3) = 2.0
Math.floor(double a)实现的是对小数向左取整,如 Math.floor(-0.7) = -1.0,Math.floor(0.5) = 0.0, Math.floor(1.3) = 1.0
Math.round(double a)实现的逻辑是四舍五入,但是对于负数有点不一样,如 Math.round(-1.5) = -1,Math.round(-0.5) = 0,有点绕,所以为了好记点,等效为 Math.floor(a+0.5),而且返回的是整数。

2. ceil、floor源码
2.1 ceil和floor代码
因为round可通过floor来实现,所以round源码就不多加分析,主要分析ceil和floor方法,从下图我们可以知道ceil和floor方法实际上都是调用floorOrCeil方法实现,只是参数不一样。参数后续分析,所以我们接下来分析floorOrCeil这个方法。

2.2 floorOrCeil源码
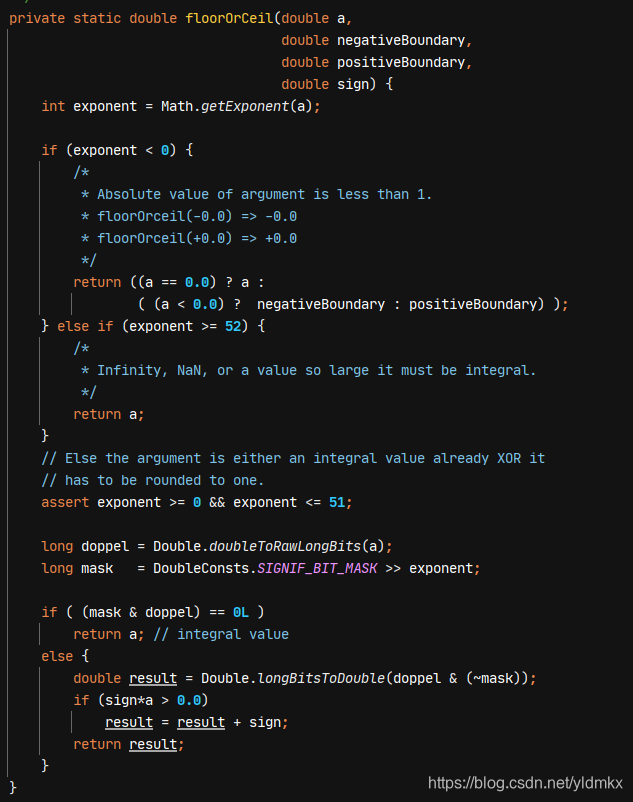
看了源代码,有点复杂,接下来我们一段一段分析

2.2.1
int exponent = Math.getExponent(a);这个方法是得到浮点数a的指数部分,这个指数不是我们的科学计算法中的以10为底的指数,这个指数是以2为底的指数。不懂就举例,如82.2的指数为6,0.23的指数为 -3,-0.1的指数为 -4,-6.3的指数为2,这个是怎么算的?
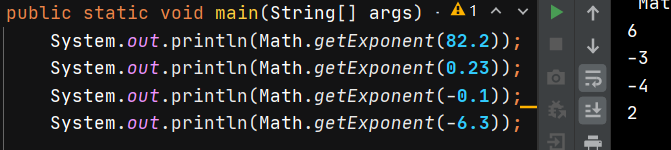
不知道怎么算出来的,那我们反推一下这些数字用指数怎么表示的,如下图,不知道你们能不能看懂,如果看不懂慢慢分析一下吧,讲也不太好讲。

2.2.2

在知道指数怎么算出来后,我们应该知道指数小于0的情况是什么了,其实就是浮点数范围处于 -1<a<1,接下来用到了三目运算符 a ?b:c,如果a==0.0,注意 -0.0=0.0, 直接返回a ,如果不是0.0,判断是负数还是整数,如果是负数取负边界,如果是正数,取正边界。这个时候用到了我们前面提到的floorOrCeil参数问题,我们先考虑如果是ceil方法,ceil方法调用floorOrCeil,传入的负边界是 -0.0,正边界是1.0,那么负数取负边界得到 -0.0,整数取正边界得到 1.0,刚好是向右取整;如果是floor调用floorOrCeil,传入的负边界是 -1.0,正边界是0.0,负数取负边界 -1.0,整数取正边界 0.0,刚好是向左取整。
2.2.3
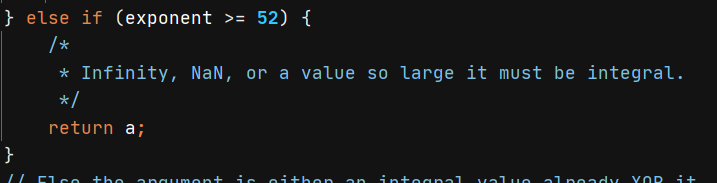
如果指数大于52会怎么样呢?这里涉及浮点数的底层存储了,接下来请仔细阅读,如下图。
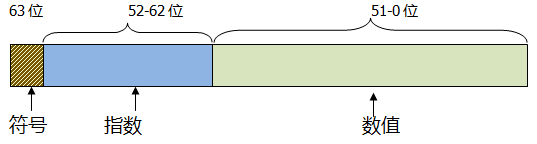
一个double浮点数8个字节64位,一位符号位,11位存放指数值,52位存放数值,不懂就举例。比如76.3,十进制小数转为二进制不懂的可以看我另一篇博客,76.3转为二进制是 100 1100.01001 1001 1001... (1001一直循环),和以10为底的指数原理一样,这个数字以2为底的指数知道是几位吗?对的,指数段是6,使用了指数,以2为底的指数,我们用P来表示,那么76.3就变为了 1.00110001001 1001 1001...P6。然后接下来76.3的64位是怎么存储的呢?符号位是0,指数是6,但是还要加上 1023,也就是1029,指数段二进制表示是 10000000101,然后数值段记录的数据是小数位,也就是 1.00110001001 1001 1001...E6截取 00110001001 1001 1001... 部分,要完整表示52位的话,数值段二进制则是 0011 0001 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011,至此,我们得到了76.3的二进制表示,接下来我们通过代码验证一下,如下。

现在我们来谈谈如果指数位大于等于52会怎么样?当指数位等于52时,那么数值段存的内容都是整数部分的二进制,小数部分根本没有存,所以会有官方注释提的“a value so large it must be integral”,也就是说这个浮点数小数部分在52位数值段得不到存储,所以认为是整数,那么就直接return。
2.2.4

“assert exponent >= 0 && exponent <= 51;”没什么好说的,进一步判断指数位是否处于0和51之间。从if语句中的mask和doppel相与和0比较,我们可以推断程序是想判断浮点数的小数部分是不是都是0,如果小数部分是0,我们可以直接返回。经过上面对浮点数的存储分析,我们怎么得到浮点数的小数部分呢?
首先,小数部分在数值段存储,但是指数部分也在数值段中存储,因为我们可以得到指数部分的位数,这样我们就可以通过向左移位把指数段的11位和数值段的指数部分移除,注意:符号位是不会被移除的。所以如果是负数的话,我们在移位结束之后还得把二进制的首位符号位去掉。
源码中首先通过Double.doubleToRawLongBits(a)求得浮点数的二进制表示 0100 0000 0101 0011 0001 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011,然后将DoubleConsts.SIGNIF_BIT_MASK >> exponent向右移动,其中DoubleConsts.SIGNIF_BIT_MASK是个常量,数值大小如下图,exponent是6。因此得到二进制表示 0000 0000 0000 0000 0011 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111。然后进行 与 运算,最后得到浮点数的小数部分二进制表示为 0000 0000 0000 0000 0001 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011,然后再和0比较,如果相等,说明小数部分是0,那么说明这个浮点数其实是个整数,直接return。
![]()
2.2.5
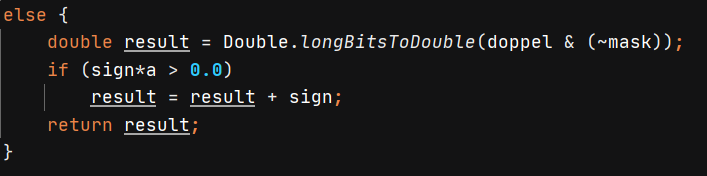
终于来到了最后,上面计算得到小数部分不是0,那我们需要先得到浮点数的整数部分,然后再考虑是向右取整还是向左取整 。先前求得的mask小数部分的二进制位全是1,现在取反则是符号位、指数段和数值段指数部分的二进制是1,那么 (~mask)的二进制表示是 1111 1111 1111 1111 1100 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,和doppel进行与运算得到 0100 0000 0101 0011 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,该二进制表示为76.0。紧接着判断是ceil还是floor,如果是ceil,那么sign是1.0,然后如果浮点数是负数,我们刚刚取整相当于已经向右取整,只考虑正数,所以sign*a>0.0,整数+1(sign是 1.0);如果是floor,那么sign是 -1.0,然后如果浮点数是正数,我们刚刚取整相当于已经向左取整,只考虑负数,所以sign*a>0.0,整数-1(sign是 -1.0),到此源码分析结束。
3. 自己重写实现ceil和floor以及round方法
我们自己重写的话,主要是取整那一块代码可以修改,其它的比较简单容易理解也不需要重写。所以,我们有什么方法可以取出浮点数的整数部分呢?
public static double ceilOrFloor(double a, double negative, double positive, double sign){
int exp = Math.getExponent(a);
if(exp<0){
return (a==0.0) ? a : (a<0.0 ? negative : positive);
}else if(exp>51){
return a;
}
String s = String.valueOf(a);
String s2 = s.substring(0, s.indexOf('.'));
double result = Double.valueOf(s2);
if(a==result){
return a;
}else{
if(sign*a > 0.0)
result += sign;
return result;
}
}
public static double floor(double a){
return ceilOrFloor(a, -1.0, 0.0, -1.0);
}
public static double ceil(double a){
return ceilOrFloor(a, -0.0, 1.0, 1.0);
}
public static long round(double a){
return (long)floor(a+0.5);
}部分测试结果如下
