Pytorch实现线性回归（调包）

前言

pytorch调包实现线性回归

过程如下

#导包
import torch.nn as nn
import torch
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

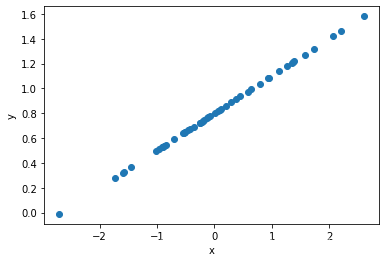
1准备数据

x=torch.randn([50,1])#50个随机数 范围在0-1之间
y=x*0.3+0.8

plt.figure()
plt.scatter(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

2准备模型

class Lr(nn.Module):#继承nn.module
    def __init__(self):
        super(Lr,self).__init__()
        self.linear=nn.Linear(1,1)
        
    def forward(self,x):
        out=self.linear(x)
        return out 

#实例化一个模型
model=Lr()
#实例化一个损失函数
criteron=nn.MSELoss()
#实例化一个优化器
optimizer=optim.SGD(model.parameters(),lr=1e-3)#这里用SGD   

3循环迭代

for i in range(3001):
    y_predict=model(x)#y的预测值
    loss=criteron(y,y_predict)#计算loss
    optimizer.zero_grad()#梯度清0
    loss.backward()#反向传播
    optimizer.step()#更新参数
    if i%300==0:
        print('迭代次数:',i,'\t误差',loss.data)

迭代次数: 0 误差 tensor(3.5595)
迭代次数: 300 误差 tensor(1.0377)
迭代次数: 600 误差 tensor(0.3026)
迭代次数: 900 误差 tensor(0.0883)
迭代次数: 1200 误差 tensor(0.0258)
迭代次数: 1500 误差 tensor(0.0075)
迭代次数: 1800 误差 tensor(0.0022)
迭代次数: 2100 误差 tensor(0.0006)
迭代次数: 2400 误差 tensor(0.0002)
迭代次数: 2700 误差 tensor(5.5652e-05)
迭代次数: 3000 误差 tensor(1.6422e-05)

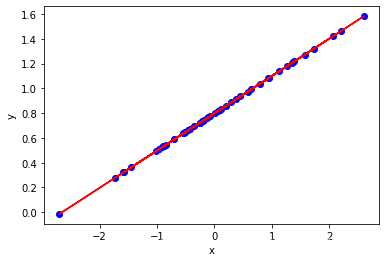
4效果可视化

model.eval()#进入评估模式
predict=model(x)#模型的输出
output=predict.detach().numpy()#转成数据准备画图

plt.figure()
plt.scatter(x,y,c='b')#原始的数据 蓝色
plt.plot(x,output,c='r')#拟合的数据 红色
plt.xlabel('x')
plt.ylabel('y')
plt.show()

总结

（如果您发现我写的有错误，欢迎在评论区批评指正）。