VarianceThreshold、pearsonr、PCA、LDA(特征工程之特征降维)

前言

特征降维是指在某些限定条件下，降低随机变量（特征）的个数，得到一组“不相关”的主要变量的过程。比如一辆车的购买时间和行驶路程就有很强的相关性。因为在进行机器学习算法模型进行训练的时候，都是通过特征进行学习，如果特征本身存在问题或者特征之间相关性较强，对算法模型训练有很大的影响。所以要进行特征的选择（或者说降维）、主成分分析PCA等，目的是从数据集中的特征中找出主要特征。
本文是特征降维，包括删除低方差数据以及变量相关性的计算。（PCA、LDA见另外一篇博文）

一、过滤低方差特征(VarianceThreshold())

什么叫低方差数据以及为什么要删除地方差数据？举个栗子，在大学录取高考学生的时候，会根据学生的语文、数学、英语、理综（文综）的分数来进行筛选，实际上就是4个特征加权之后的结果，判断是否录取。假如这里再添加一个特征：学生的年龄，这个特征是否合适？显然是不合适的，因为高三的学生年龄大学绝大部分都在18左右，这个特征加进来就显得冗余。这个特征的存在对最终的结果没有什么影响，但是在算法训练过程中也会消耗内存，甚至干扰最终的模型的训练，所以最好把它给删除。
特征方差小：某个特征大多样本值比较接近（去掉）；
特征方差大：某个特征很多样本值都有差别（保留）。
举例如下，有一组数据，把方差较低的特征给去掉。

#低方差过滤
import pandas as pd
##列名与数据对齐显示
pd.set_option('display.unicode.ambiguous_as_wide', True)
pd.set_option('display.unicode.east_asian_width', True)

#1先准备好数据
myindex=pd.Index(data=['1','2','3','4','5','6','7','8','9','10'],name='标号')
mydata={
    
    
    '行程':[1234,4235,3214,3421,4312,2341,3214,1432,1423,4211],
    '油耗':[14,35,32,21,41,25,32,42,12,13],
    '时间':[0.3,1.4,1.8,2.4,3.1,0.6,0.7,0.1,0.5,4.0],
    '年龄':[25,25,26,25,25,26,25,25,26,27],
}
myown=pd.DataFrame(data=mydata,index=myindex)
print("看一下myown:\n{}\n及其维度{}".format(myown,myown.shape))

from sklearn.feature_selection import VarianceThreshold
#2实例化一个转换器
transfer=VarianceThreshold(threshold=1)#设置threshold=1，把数据方差低于1的特征删除
#3调用一个transform
data_new=transfer.fit_transform(myown)
import numpy as np
np.set_printoptions(precision=3,suppress=True)#设置小数点显示精度，保留三位小数
print("看一下datanew:\n{}\n及其数据维度:{}".format(data_new,data_new.shape))

这样就把年龄那组数据给删除了（设置了VarianceThreshold(threshold=1)，把方差低于1的数据给删除了）。

#再把列索引加进去
data_new=pd.DataFrame(data=data_new,index=myindex,columns=['行程','油耗','时间'])
print('再把列索引加进去:\n{}'.format(data_new))

这样就得到了一组剔除指定低方差的数据，为后续的机器学习算法调优做准备。

二、相关系数pearsonr的计算

除了过滤掉低方差的数据，有时候还有两组数据相关性很强的情况，也会干扰模型的调优。比如本文开头所说，一个汽车的购买时间和行驶路程是有很强的相关性的，相关性的特征太多会造成数据的冗余，处理起来很不方便。所以要去除相关性强的特征，只保留其中的少数或者1个。
那么怎么知道两个特征之间的相关性的强弱呢？可以通过皮尔逊相关系数来衡量（下图来自百度百科）：

有没有发现这哥们儿很眼熟！在这儿呢！

看到它有没有让你回忆起峥嵘的大二岁月或者艰辛的考研岁月？
当然了，工作以后不用像学生时代那样手动去计算了，可以用计算机帮忙解决，举例如下：

#准备数据
import numpy as np
x=np.arange(1,11)#x是1-10的整数
y=2*x+1#y是有x的一次函数关系，所以线性关系很强的
z=np.random.randint(1,100,10)#z是随机数，所以跟x线性关系不大
print('x的值:{}\ny的值：{}\nz的值:{}'.format(x,y,z))

x的值:[ 1 2 3 4 5 6 7 8 9 10]
y的值：[ 3 5 7 9 11 13 15 17 19 21]
z的值:[46 42 9 27 72 21 17 21 82 37]

#数据可视化一下
import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.title("y与x之间的关系")
plt.scatter(x,y)
plt.subplot(2,1,2)
plt.title("z与x之间的关系")
plt.scatter(x,z)
plt.show()

from scipy.stats import pearsonr#导入pearsonr包计算
print('x与y之间的皮尔逊系数:{}'.format(pearsonr(x, y)))
print('x与z之间的皮尔逊系数:{}'.format(pearsonr(x, z)))
#皮尔逊系数（a,b）a>0表示正相关，a<0表示负相关.绝对值在-1到1之间
#绝对值越接近于1表示相关性越强。b表示显著性，越小代表线性相关想显著性越强

x与y之间的皮尔逊系数:(1.0, 0.0)
x与z之间的皮尔逊系数:(0.5417714436829721, 0.10574924671054783)
用这种方法可以计算两个特征之间的相关性强弱，为后续的机器学习算法做铺垫。

三、特征降维PCA与LDA

3.1主成分分析PCA

主成分分析PCA(Principal Components Analysis)是将数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。应用在回归分析或者聚类分析中：
降维：降低高维数据，简化计算，达到数据降维，压缩，降噪的目的，数据的维度减少了，但是尽可能的保留了最大的信息，把一些不重要的特征去掉；
聚类：把复杂的多维数据点，简化成少量的数据点，易于分簇。
PCA的直观理解，如下图的水壶，有4张图片，请问选哪一张能更好的表达出这个水壶的特征呢？显然是最后一张，因为它保留了最多的信息。PCA要达到的目的也是这样（横看成岭侧成峰，不如45度角摆pose）。

将原有的d维数据转换成k维的数据，k<<d，并且新生的k维数据尽可能多的包含原来d维数据的信息。
假如对于给定的5个点，数据如下：(-1,-2)、(-1,0)、(0,0)、(2,1)、(0,1)，在二维平面中选择一个方向的直线，如何选择这个方向，才能保留最多的信息呢。就是原来的点投影在这个直线上之后的投影值尽可能的分散，就是原来的点在这个直线上投影之后的投影值的方差大，方差大说明保留了更多的原始信息。


当然了，也不用每次都用手动去计算。可以使用计算机运算，举例如下：

#准备一下数据
data=[[2,8,4,5],[6,3,0,8],[5,4,9,1]]
print("看一下data的值：{}及其维度:{}".format(data,len(data)))

看一下data的值：[[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]及其维度:3

from sklearn.decomposition import PCA
#实例一个转换器,n_components=2就是把原来的数据降成2维
transfer=PCA(n_components=2)
data_new=transfer.fit_transform(data)#调用fit_transform
print("看一下data_new:\n{}\n及其类型:{}".format(data_new,type(data_new)))
print('4个特征就按照要求转换成2个特征了')

看一下data_new:
[[ 1.28620952e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
及其类型:<class ‘numpy.ndarray’>
4个特征就按照要求转换成2个特征了

#实例一个转换器,n_components=3就是把原来的数据降成3维
transfer2=PCA(n_components=3)
data_new2=transfer2.fit_transform(data)
print("看一下data_new2:\n{}\n及其类型:{}".format(data_new2,type(data_new2)))
print('4个特征就按照要求转换成3个特征了')

看一下data_new2:
[[ 1.28620952e-15 3.82970843e+00 5.26052119e-16]
[ 5.74456265e+00 -1.91485422e+00 5.26052119e-16]
[-5.74456265e+00 -1.91485422e+00 5.26052119e-16]]
及其类型:<class ‘numpy.ndarray’>
4个特征就按照要求转换成3个特征了

#实例一个转换器,n_components=0.95就是把原来的数据95%的信息
transfer3=PCA(n_components=0.95)
data_new3=transfer3.fit_transform(data)
print("看一下data_new3:\n{}\n及其类型:{}".format(data_new3,type(data_new3)))
print('0.95是小数表示保留百分之多少的信息')

看一下data_new3:
[[ 1.28620952e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
及其类型:<class ‘numpy.ndarray’>
0.95是小数表示保留百分之多少的信息

3.2线性判别分析LDA

线性判别分析LDA(Linear Discriminant Analysis)可以作为特征的降维方法，也可以作为分类方法。LDA作为特征降维工具的原理是，根据带标签的数据点，通过投影的方法，投影到维度更低的空间中，使得投影后的点，按照类别进行区分，同一类别的数据点，在投影后的空间中更接近。

LDA数学推导以后有机会补充。
LDA应用举例：

#将iris数据降到2维
#先导入数据
from sklearn.datasets import load_iris
myiris=load_iris()

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda=LinearDiscriminantAnalysis(n_components=2)#实例化一个LDA转换器
new_iris_data=lda.fit_transform(myiris.data,myiris.target)
print("经过LDA降维成两维之后维度:{}".format(new_iris_data.shape))

经过LDA降维成两维之后维度:(150, 2)

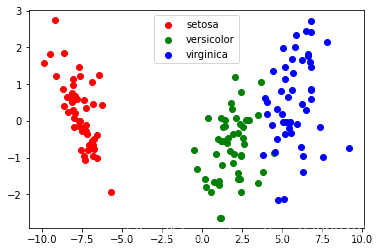
import matplotlib.pyplot as plt
plt.figure()
for c, i, target_name in zip("rgb", [0, 1, 2], myiris.target_names):
    plt.scatter(new_iris_data[myiris.target == i, 0], new_iris_data[myiris.target == i, 1], c=c, label=target_name)
plt.legend()
plt.show()

总结

本文主要讲了特征的降维，包括过滤地方差的特征，以及怎么计算两个变量特征之间相关性的强弱；之后介绍了一下PCA和LDA以及怎么调包。为后续的机器学校算法做铺垫！（如果您发现我写的有错误，欢迎在评论区批评指正）。