Leetcode 不同路径

不同路径

题目描述：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

题目链接

示例

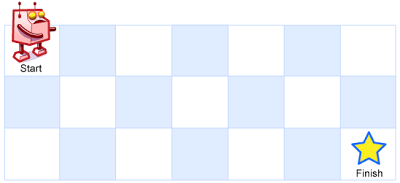
结果：28种

class Solution {
    
    
    public int uniquePaths(int m, int n) {
    
    
        // 初始化
        int[][] dp = new int[m][n]; // 路径数矩阵
        for(int i = 0 ; i<n ; i++){
    
    
            dp[0][i] = 1; // 机器人走最上面只有一种可能
        }
        for(int i = 0 ; i<m ; i++){
    
    
            dp[i][0] = 1; // 机器人走最左边只有一种可能
        }
        // 动态规划过程
        for(int i = 1 ; i<m ; i++){
    
    
            for(int j = 1 ; j<n ; j++){
    
    
                dp[i][j] = dp[i-1][j]+dp[i][j-1]; // 当前路径数等上面的路径数和左边的路径数之和
            }
        }
        return dp[m-1][n-1];
    }
}

很容易想到，该题目是一个动态规划题目，因为每次的位置的路径数等于从上面到当前位置的路径数和从左边到当前位置的路径之和，即：

dp[i][j] = dp[i-1][j] (上到下) + dp[i][j-1] (左到右)