了解完美二叉树

    在本教程中，您将学习完美二叉树。此外，您还将找到C语言中完美二叉树的示例。
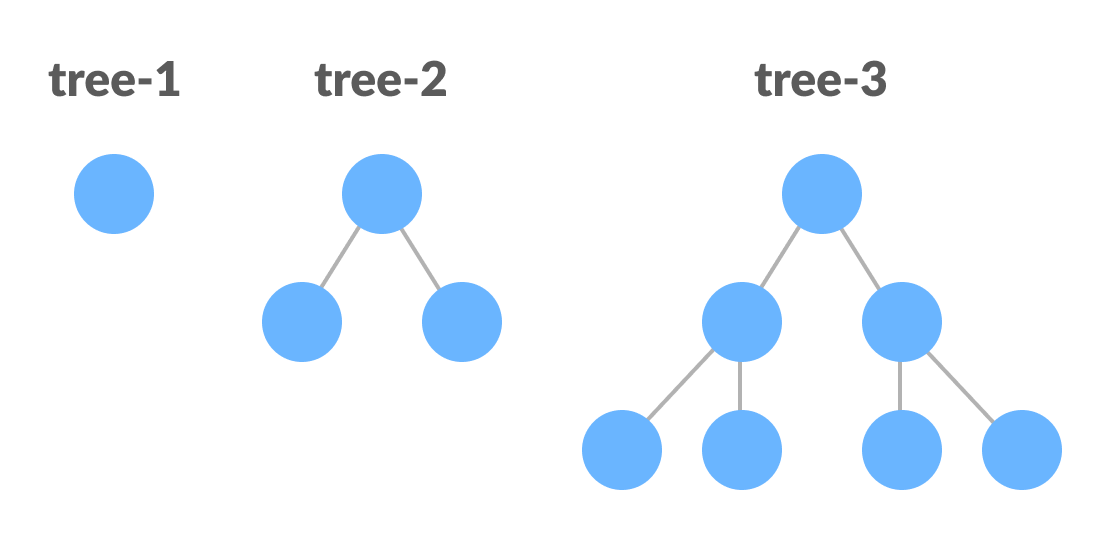
    完美二叉树是一种二叉树，其中每个内部节点正好有两个子节点，所有叶节点处于同一级别。

    所有内部节点的度数都是2。
    完美二叉树可以被定义为：

1. 如果单一节点没有子节点，则它为高度h = 0 的完美二叉树。
2. 如果节点 h > 0，如果它的两个子树的高度都是 h-1 并且不重叠，那么它就是一个完美二叉树。

C示例

    以下代码用于检查是否是完美二叉树。

// Checking if a binary tree is a perfect binary tree in C

#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>

struct node {
    
    
  int data;
  struct node *left;
  struct node *right;
};

// Creating a new node
struct node *newnode(int data) {
    
    
  struct node *node = (struct node *)malloc(sizeof(struct node));
  node->data = data;
  node->left = NULL;
  node->right = NULL;

  return (node);
}

// Calculate the depth
int depth(struct node *node) {
    
    
  int d = 0;
  while (node != NULL) {
    
    
    d++;
    node = node->left;
  }
  return d;
}

// Check if the tree is perfect
bool is_perfect(struct node *root, int d, int level) {
    
    
    // Check if the tree is empty
  if (root == NULL)
    return true;

  // Check the presence of children
  if (root->left == NULL && root->right == NULL)
    return (d == level + 1);

  if (root->left == NULL || root->right == NULL)
    return false;

  return is_perfect(root->left, d, level + 1) &&
       is_perfect(root->right, d, level + 1);
}

// Wrapper function
bool is_Perfect(struct node *root) {
    
    
  int d = depth(root);
  return is_perfect(root, d, 0);
}

int main() {
    
    
  struct node *root = NULL;
  root = newnode(1);
  root->left = newnode(2);
  root->right = newnode(3);
  root->left->left = newnode(4);
  root->left->right = newnode(5);
  root->right->left = newnode(6);

  if (is_Perfect(root))
    printf("The tree is a perfect binary tree\n");
  else
    printf("The tree is not a perfect binary tree\n");
}

完美二叉树定理

1. 高度为h的理想二叉树具有$2^{h+1}–1$节点。
2. 具有n个节点的完美二叉树具有高度log(n + 1) – 1 = Θ(ln(n))。
3. 高度为h的完美二叉树具有$2^h$个叶节点。
4. 完美二叉树中节点的平均深度为Θ(ln(n))。

参考文档

[1]Parewa Labs Pvt. Ltd.Perfect Binary Tree[EB/OL].https://www.programiz.com/dsa/perfect-binary-tree,2020-01-01.