【LeetCode134】-加油站

方法一

实现思路

从总体上看gas的和就是总共可以获得的汽油数，cost的和就是总共消耗的油量，当总cost大于总gas的时候明显说明从任意地点出发都无法到达

每一加油站位置的gas值将去cost值得到的就是除去到下一站消耗的油量得到的净油量

起始点需要满足的条件

1. 净油量大于0
   起始位置由于之前没有别的油量的积累，所以起始点的净油量一定是大于0的
2. 从起始点开始累积的净油量一定大于等于0
   净油量的累加代表的是走到当前这步，剩余的油量，剩余油量如果小于0那么一定意味着油量不足以到达该点，所以起始点需要满足每走一步累积的净油量是大于等于0，等于0说明到达该点油量恰恰好好

实现代码

class Solution {
    
    
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
    
    
        int n=gas.size();
        int sum_gas=0,sum_cost=0;
        int flag=-1;
        int max=0;
        vector<int> gap(n,0);
        vector<int> plus;
        for(int i=0;i<n;i++){
    
    
            sum_gas+=gas[i];
            sum_cost+=cost[i];
            gap[i]=gas[i]-cost[i];
            if(gap[i]>=0){
    
    
                plus.push_back(i);
            }
        }
        if(sum_cost>sum_gas) return -1;
        for(int i=0;i<plus.size();i++){
    
    
            int ff=0;
            int sum=0;
            for(int j=0;j<n;j++){
    
    
                int index=(j+plus[i])%n;
                sum+=gap[index];
                if(sum<0){
    
    
                    ff=1;
                    break;
                }
            }
            if(!ff) return plus[i];
        }
        return -1;
    }
};

提交结果及分析

最坏的时间复杂度为O（n^2）

方法二

实现思路

暴力的枚举从每一个点都当作起点的情况

实现代码

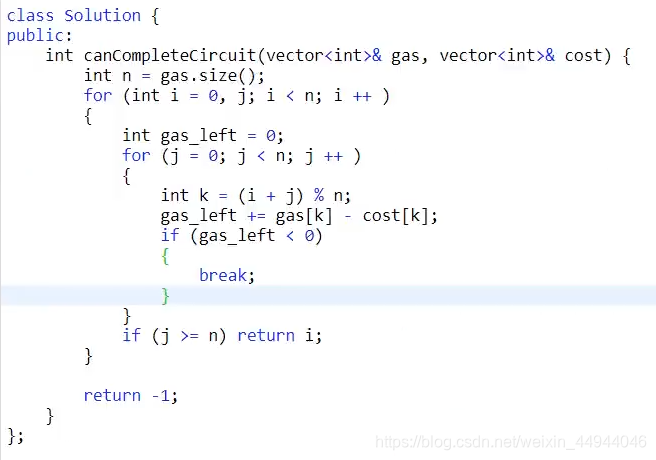
分析

时间复杂度O（n^2）

优化

主要更改的位置再i不是单纯的i++而是i+=j+1
优化思想 如果i走到j失败了，i和j之间的任意起点开始都会失败，所以直接令i从i+j+1开始
原理在于但从i+1来看，从i走到j的时候，由于可以从i走到i+1，说明到i+1的时候油量是大于等于0，有一个额外的油量。在这种有额外油量的情况下走到j都不可行，直接从i+1走到j的时候，没有额外的油量了更不可能走到j了
时间复杂度
O（n），i和j总共加起来大致为n